水轮机及其调速器特性对孤立电网频率特性的影响

曹炜，祁晓卿，王大宏，王大飞，靳希，顾丹珍

（1.上海电力学院电力与自动化工程学院，上海200090; 2.西藏电力有限公司，西藏拉萨 850000）

目前，我国西藏地区孤立电网（如阿里电网）的主要电源是小型水轮发电机组，并带有少量备用柴油机组，电网中的负荷量较小且多为居民负荷，对频率质量的要求不高.为了保证用户的正常用电和电网的安全稳定运行，仍需对孤立电网的频率进行有效的控制［1，2］.

本文基于电力系统分析综合程序（Power System Analysis Software Package，PSASP），对西藏阿里电网进行建模，并在大负荷冲击下进行仿真计算，研究水轮机及其调速器特性对电网频率特性的影响，以期为探索阿里电网中合适的频率控制策略提供依据.

1 阿里电网与仿真模型简介

阿里电网是一个典型的孤立小电网，其主要电源是狮泉河水电站，装机容量为4×1.6 MW，通过4台2 MW的升压变压器将电压升至35 kV后，经输电线路送电到阿里地区的狮泉河镇.该电网的主要负荷集中在狮泉河镇上，截至2009年最大负荷约为3.3 MW.在狮泉河镇配网中，有一些用户自备柴油发电机（总容量为1.86 MW），当水电站故障时由备用柴油发电机供电，同时实行限电.

本文用PSASP软件建立阿里电网模型，假设运行方式为水轮机开机3台（额定功率为3×1.6 MW），负荷总量为3 MW，35 kV和10 kV侧的负荷量分别为1 MW和2 MW.

1.1 发电机及其励磁系统模型

本仿真模型采用PSASP的3型水轮发电机模型，即考虑Eq″，Ed″，Eq'电势变化的5阶模型，此模型适合于凸极转子（水轮）发电机.励磁系统模型为自并励和自复励的快速系统及可控硅调节器，对应选用PSASP中的2型励磁系统.

1.2 调速器模型

选用PSASP软件中提供的Ⅰ型原动机调速器模型，其简化传递函数如图1所示.

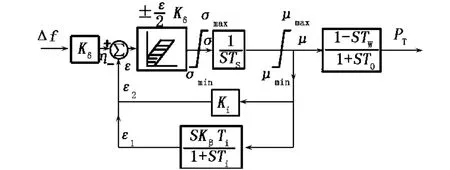
图1 PSASP I型调速器简化传递函数

令T0=0.5Tw，则水轮机部分的传递函数为：

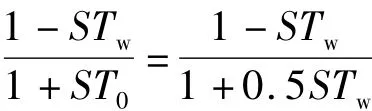
1.3 负荷模型

负荷模型采用5型综合负荷模型，构成比例为70%恒定阻抗和30%感应电动机模型，35 kV和10 kV侧均采用该比例.其中，感应电动机的参数采用PSASP中的典型参数［3］.

2 水轮机及其调速器参数对阿里电网频率特性的影响

阿里电网中的最大负荷为550 kW的阻性负荷，仿真计算此负荷突然投入时阿里电网的频率特性.计算过程中，水轮机及其调速器各参数基本设置如表1所示［4-7］，每次测试只改变表1中的某一项参数，并保证其他参数不变.

表1 水轮机及其调速器的基本参数

2.1 转子惯性时间常数

改变水轮发电机转子惯性时间常数Tj，保持其他参数不变，系统在负荷突增冲击下的频率动态响应曲线如图2所示.

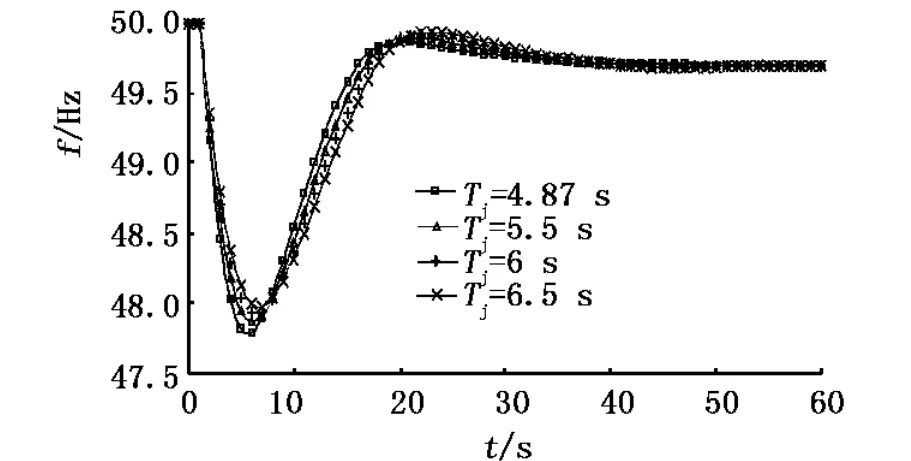
图2 转子惯性时间常数变化时的频率动态响应曲线

由图2可以看出，随着机组惯性时间常数的增大，系统在扰动后的暂态过程中，暂态频率最大，超调量逐渐减小，动态调节过程变得缓慢，系统达到稳态频率的时间逐渐变长，但稳态频率保持不变，约为49.7 Hz.

2.2 测量环节放大倍数

水轮机调速器的测速部件灵敏度一般为0.05～0.1［6］，对应图1中测量环节放大倍数Kδ为10～20.改变Kδ且保持其他参数不变，系统在负荷突增冲击下的频率动态响应曲线如图3所示.

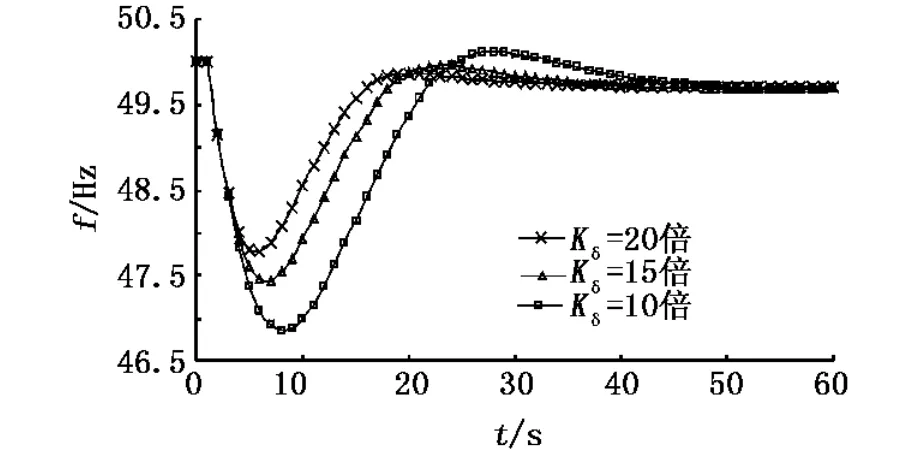
图3 测量环节放大倍数变化时的频率动态响应曲线

由图3可以看出，随着测量环节放大倍数Kδ的增大，系统在发生扰动时的频率最大超调量（暂态频率的最大偏差值）将变小，系统达到稳态频率的时间缩短，而稳态频率仍约为49.7 Hz.

2.3 伺服机构（主接力器）时间常数

水轮机调速器的伺服机构时间常数Ts一般为4～7 s［6］，改变Ts且保持其他参数不变，系统在负荷突增冲击下的频率动态响应曲线见图4.

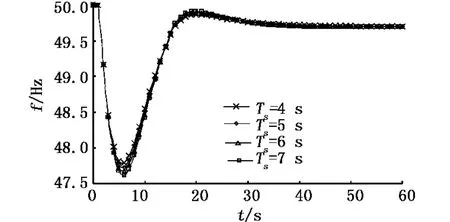
图4 伺服机构时间常数变化时的频率动态响应曲线

结合图1可知，配压阀的活塞位移σ的变化造成接力器活塞位移μ的变化，二者之间的关系为：

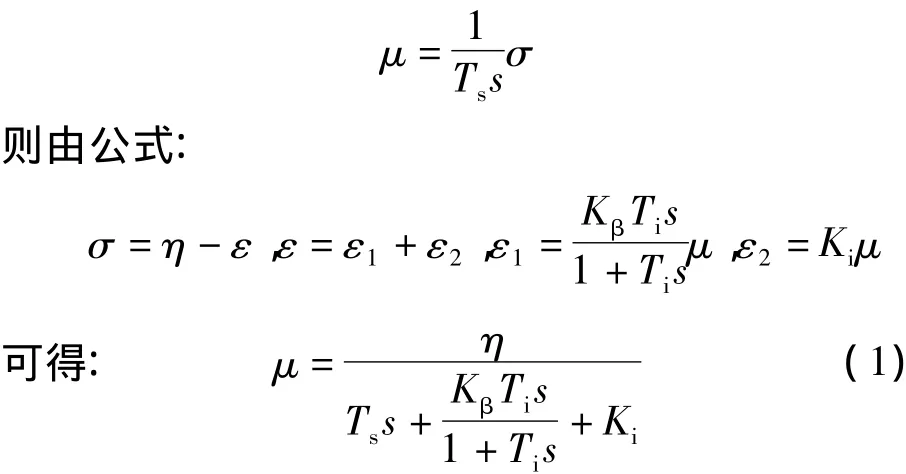
由式（1）可知，若频率偏差Δf不变，测量环节的放大倍数Kδ不变，则η不变.由于Kβ，Ti，Ki均不变，则Ts的增加将导致μ的减小，即接力器活塞位移减小，造成导水叶开度减小，从而使水轮机输出的功率Pm增加的速度变慢，导致系统超调量变大.但稳态频率保持不变，约为49.7 Hz.

2.4 水流惯性时间常数

水流惯性时间常数一般为0.5～4 s［6］，保持其他参数不变，则阿里电网在受到负荷突增冲击时的频率动态响应特性曲线如图5所示，其机械功率Pm的输出响应曲线如图6所示.

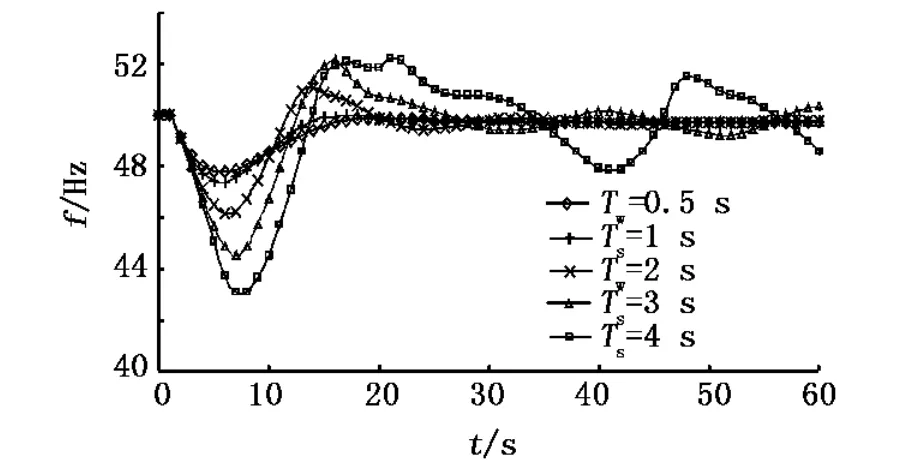
图5 水流惯性时间常数变化时的频率动态响应曲线

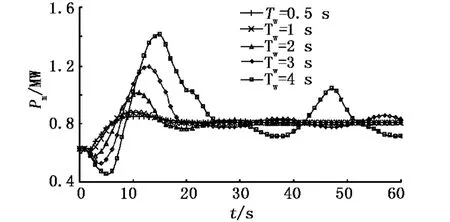
图6 水流惯性时间常数变化时机械功率的输出曲线

由图5和图6可知，随着水流惯性时间常数的增大，水锤效应显著，系统在发生扰动时的频率最大超调量将变大，系统达到稳态频率所用的时间也越长.若水锤为3 s或4 s，则会导致该孤立电网暂态过程超调时间延长，频率会大幅振荡.

2.5 水锤效应

在动态过程中，当水轮机导叶开启时，引水系统水流的加速将导致水轮机力矩有短时段的降低，从而产生与控制目标相反的逆向调节，这将为系统的动态稳定和相应特性带来十分不利的影响.因此，随着水锤效应时间常数的增大，水轮机系统动态特性将会恶化，系统的一次调频性能将变差［8］.

有无水锤效应时孤立电网的频率动态响应特性曲线如图7所示，水轮机机械功率Pm的输出响应曲线如图8所示.

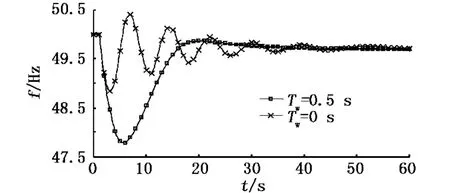
图7 有无水锤效应时的频率动态响应曲线

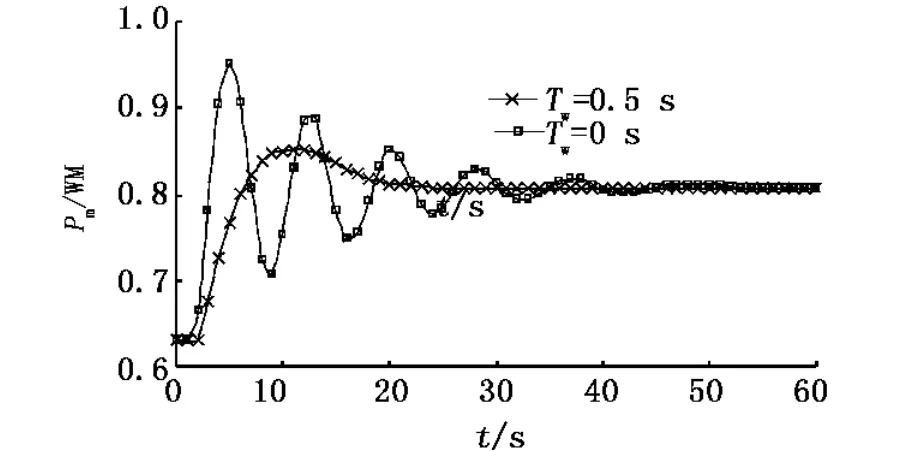
图8 有无水锤效应时的机械功率输出曲线

由以上仿真结果可以看出，若水轮机无水锤效应，则机组的出力可以迅速增加，系统的暂态频率超调量将变小，但振荡次数有所增加，达到稳态频率所需时间较长，其稳态频率与水轮机有水锤效应时相同，仍约为49.7 Hz.

3 结论

（1）水轮发电机组惯性时间常数、测量环节放大倍数、水锤效应及水流惯性时间常数对孤立电网的暂态频率变化特性影响较大，其中水锤效应的影响最大，但上述各参数并不影响由调差系数决定的系统稳态频率偏差;

（2）加大水轮发电机组的惯性时间常数，有利于改善系统的频率特性.在实际应用中，虽然不能改变单台机的惯性时间常数，但可以考虑尽量多开机，增加一定负载功率下的系统等效惯性时间常数.

［1］杨冠城.电力系统自动装置原理［M］.第四版.北京：中国电力出版社，2007：139-149.

［2］中华人民共和国国家质量监督检验检疫总局.GBT 15945-2008电能质量电力系统频率偏差［S］.北京：中国标准出版社，2008：1-3.

［3］朱方，汤涌，张东霞，等.发电机励磁和调速器模型参数对东北电网大扰动试验仿真计算的影响［J］.电网技术，2007，31 （4）：69-74.

［4］倪以信.动态电力系统的理论和分析［M］.北京：清华大学出版社，2002：72-80.

［5］李华，史可琴，范越，等.电力系统稳定计算用水轮机调速器模型结构分析［J］.电网技术，2007，31（5）：25-28.

［6］西安交通大学，清华大学，浙江大学，等.电力系统计算［M］.北京：水力电力出版社，1978：127-155.

［7］PRABHA KUNDUR.Power system stability and control［M］.北京：中国电力出版社，2001：377-460.

［8］魏守平.水轮机调节［M］.武汉：华中科技大学出版社，2009：77-129.

（编辑白林雪）