纤维失效对陶瓷基复合材料准静态加卸载迟滞回线的影响
李龙彪 宋迎东
(南京航空航天大学能源与动力学院,南京,210016,中国)
INTRODUCTION
Ceramic materials possess high strength and modulus at elevated temperatures.But their use as structural components is severely limited because of their brittleness.Continuous fiber reinforced ceramic matrix composites not only exploit their attractive high-temperature strength but also reduce the propensity for catastrophic failure. These materials have already been implemented on some aero engines components[1].
Upon quasi-static unloading and subsequent reloading,stress-strain hysteresis develops due to the frictional sliding which occurs along any debonded region[2-3].Li et al.[4-5]investigated the effects of interface debonding and fiber Poisson contraction on hysteresis loops when fiber/matrix interface was chemically bonded.It is found that the completely unloading strain and the area of the hysteresis loops decrease as the increase of interface debonded energy and interface frictional coefficient.Li and Song[6-7]developed approaches to estimate interface shear stress and interface frictional coefficient of ceramic composites from hysteresis loops.It is found that the interface shear stress and interface frictional coefficient degraded as cycle increases.And the degradation rate depends on the fatigue maximum stress,the fatigue load ratio and the cycle number.It should be noted that the models mentioned above do not take into account the effect of fiber failure on the hysteresis loops.When ceramic matrix composites are under quasi-static unloading/reloading, the fracture and intact fibers both slip in the interface debonded region,which affect the shape, area and the location of the hysteresis loops[8-10].
In this paper,the effect of fiber failure on quasi-static unloading/reloading hysteresis loops is investigated by the micro mechanics approach. The hysteresis loops of different stresses with consideration of fiber failure have been compared with the cases which are not taken consideration of fiber failure.The effects of fiber strength and Weibull modulus on fiber failure,and the shape and area of the hysteresis loops have been analyzed.
1 STRESS ANALYSIS
Upon first loading to the fatigue maximum stressemax,it is assumed that matrix cracking and interface debonding occur.To analyze stress distributions in the fiber and the matrix,a unit cell is extracted from the ceramic matrix composites, as shown in Fig.1.The unit cell contains a single fiber surrounded by a cylinder of matrix.The fiber radius is rf,and the matrix radius is R(R= rf/Vf1/2). The length of the unit cell is L/2, which is just the half matrix crack space.The interface debonded length is Ld. On the matrix crack plane,fibers carry all the load(e/Vf), whereedenotes far field applied stress and Vfdenotes fiber volume fraction.The shear-lag model adopted by Budiansky-Hutchinson-Evans[11]is applied in the paper to perform the stress and strain calculations in the interface debonded region(x∈[0,Ld])and interface bonded region(x∈ [Ld, L/2]).

where Vmdenotes the matrix volume fraction,fi the fiber/matrix interface shear stress,dthe BHE shear-lag parameter,efoandemodenote fiber and matrix axial stress in the interface bonded region, respectively.

Fig.1 Unit cell of BHE shear-lag model
When fiber fails,the fiber axial stress distribution in the interface debonded region and bonded region is

where T is the intact fiber axial stress on the matrix crack plane.
2 DAMAGE MODELS
2.1 Matrix cracking
The brittle nature of the matrix material and the possible formation of initial crack distribution throughout the microstructure suggest that a statistical approach to matrix crack evolution is warranted in ceramic matrix composites.The tensile strength of the brittle matrix is assumed to be described by the two-parameter Weibull distribution where the probability of the matrix failure,Pm is[12]

whereemdenotes the tensile stress in the matrix, eR and m denote the matrix characteristic strength and matrix Weibull modulus,respectively.To estimate the instantaneous matrix crack space with increasing applied stress,we have

where L denotes the instantaneous matrix crack space and Lsatthe saturation matrix crack space. Using Eqs.(5,6),the instantaneous matrix crack space is[12]
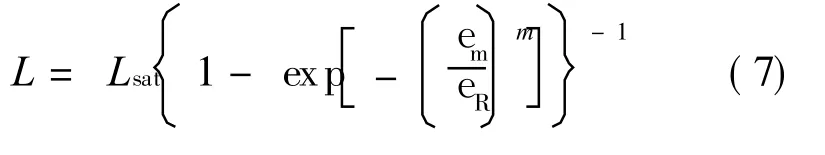
2.2 Interface debonding
When matrix crack propagates to the fiber/ matrix interface,it deflects along the fiber/matrix interface.It has been proved that the fracture mechanics approach is preferred to the shear stress approach for interface debonding[13].The fracture mechanics approach is adopted in the present analysis.The interface debonding criterion is[14]

where F=πrf2e/Vfis the fiber load at the matrix crack plane,wf(0)the fiber axial displacement at the matrix crack plane,v(x)the relative displacement between fiber and matrix.The interface debonded length Ldis
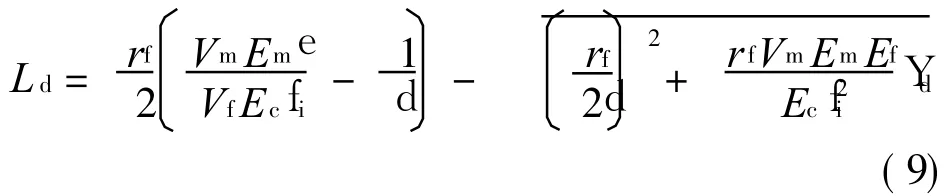
2.3 Fiber failure
There are relatively fewer models for the fiber failure of ceramic matrix composites compared with analyses for damage mechanisms such as matrix cracking and interface debonding.As fibers begin to break,the loads dropped by the broken fibers must be transferred to the intact fibers in the cross-section.The GLS assumption neglects any local stress concentrations in the neighborhood of existing breaks,and is expected to be accurate when the interface shear stress is sufficiently low.
The two-parameter Weibull model is adopted to describe fiber strength distribution,and the GLS assumption is used to determine the load carried by the intact and fracture fibers[15].

where〈Tb〉denotes the load carried by the broken fibers,and P(T)the fiber failure volume fraction[15].
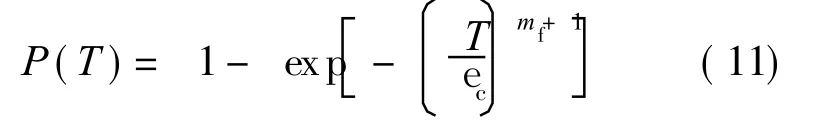
where mfis the fiber Weibull modulus,and ec the fiber characteristic strength of a length Wcof the fiber[15].

where lois the reference length,andeothe fiber reference strength of a length of loof the fiber.
When fiber fractures,the fiber stress drops to zero at the break,and the stress in the fiber builds up through the stress transfer across the fiber/matrix interface shear stress.

The sliding length lfrequired to build the fiber stress up to its previous intact value is then[15]

The probability distribution f(x)of the distance x of a fiber broken from reference matrix crack plane,provided that a break occurs within a distance±lf,is constructed based on the Weibull statistics by Phoenix and Raj[16]
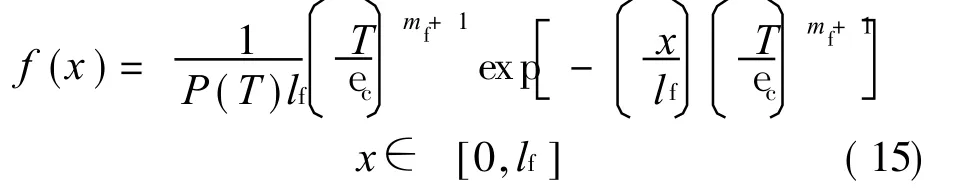
Using Eqs.(13,15),the average stress carried by the broken fiber is
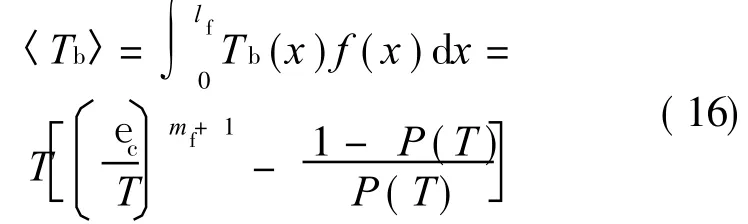
Substituting Eq.(16)into Eq.(10)leads to the form of

The load carried by the intact fibers T at the matrix crack plane for different applied stress can be obtained by solving Eq.(17),and then the fiber failure volume fraction can be obtained by substituting T into Eq.(11).When the load car-ried by the intact fibers reaches the maximum value,composites fail.The composite ultimate tensile strength eutsis

3 HYSTERESIS THEORIES
When ceramic matrix composites are under quasi-static loading,matrix cracking occurs first. As increasing the applied stress,the amounts of the matrix cracks increase. Partially matrix cracks deflect along fiber/matrix interface,and some matrix cracks propagate penetrate through fibers,which makes fiber fracture.The interface debonded length considering the effect of fiber failure is

It is shown from the Eq.(19)that,when none of the fiber fails,T=e/Vfand Ldf= Ld. When Ldf<L/2,fiber/matrix interface partially debonds.When Ldf=L/2,fiber/matrix interface completely debonds.
3.1 Interface partially debonding
When interface partially debonds,the unit cell can be divided into interface debonded region (x∈ [0,Ldf])and interface bonded region(x∈[Ldf,L/2]).Upon unloading to e(emin<e<emax),the interface debonded region can be divided into interface counter slip region(x∈ [0,y]) and interface slip region(x∈ [y,Ldf]).The unloading interface counter slip length y is

where TUdenotes the stress carried by the intact fibers at the matrix crack plane upon unloading, which satisfied the relationship of Eq.(21)


Upon reloading to e,slip again occurs near the matrix crack plane over a distance z,which denotes a new slip region.The interface debonded region can be divided into new slip region(x∈ [0, z]),counter slip region(x∈ [z,y])and slip region(x∈ [y,Ldf]). The reloading new slip length z is

where TRis the stress carried by the intact fibers at the matrix crack plane upon reloading,which satisfies the relationship of Eq.(23)

where Tmsatisfies the relationship of Eq.(24).
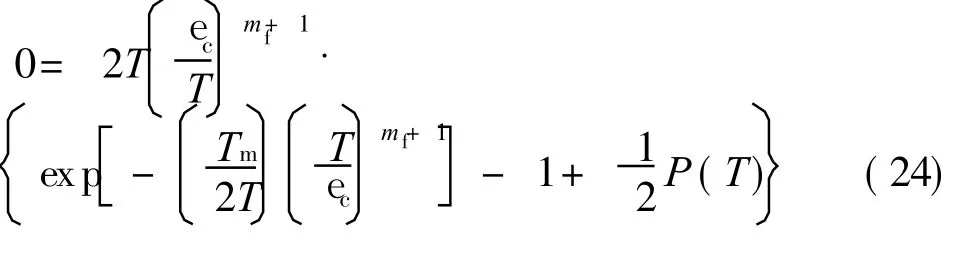
3.2 Interface completely debonding
When fiber/matrix interface completely debonds,the unit cell can be divided into interface counter slip region(x∈ [0,y])and slip region(x∈ [y,L/2])upon unloading.The unloading interface counter slip length y is
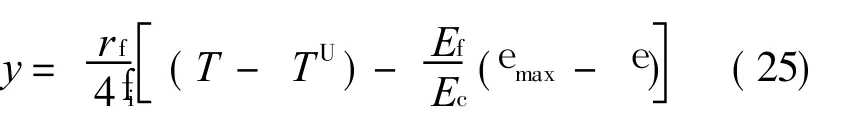
where TUsatisfies Eq.(21).
Upon reloading,the unit cell can be divided into interface new slip region(x∈ [0,z]),interface counter slip region(x∈ [z,y])and slip region(x∈ [y,L/2]). The reloading new slip length z is

where TRsatisfies Eq.(23).
3.3 Stress-strain relationship
When damage forms within the composite, the composite strain is determined from Eq.(27), which assumes that the composite strain is equivalent to the average strain in an undamaged fiber.

By the fiber axial stress during unloading and subsequent reloading,the hysteresis loops of ceramic matrix composites can be determined.
4 RESULTS AND DISCUSSIONS
The ceramic composite system of SiC/ CAS[17]is used for the case study and its basic material properties are given by Vf= 38%,Ef=210 GPa,Em=95.5 GPa,rf=7.5μm,Tf=4×10-6/°C,Tm=5×10-6/°C,Δ F=-1 000°C,Yd=0.2 J/m2,fi=15 MPa.
In the matrix statistical cracking model,the matrix cracking characteristic stresseRis derived as the Aveston-Cooper-Kelly(ACK)steady matrix cracking stress[18]
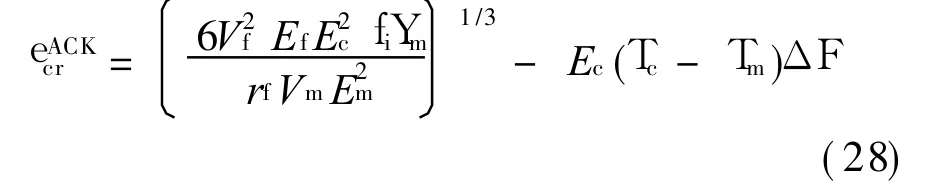
where Ym is the matrix fracture energy.Beyerle et al.[17]conducted Chervon-notched flexure tests on the SiC/CAS and yielded the matrix fracture energy,Ym= 25 J/m2.The matrix characteristic strength can be derived by Eq.(28)and given by eR=226 MPa.
The matrix crack density as a function of stress for the experimental data and present analysis are plotted in Fig.2, where the matrix Weibull modulus m is 5.The predicted results agree well with the experimental data.
Beyerle et al.[17]conducted fracture mirror experiments of the pulled-out fibers and yielded fiber characteristic strength,ec= 2.0 GPa,fiber Weibull modulus,mf=3.6.The tensile strength eutspredicted by Eq.(18)is 514 MPa,while the experimental strength is 455 MPa.To efficiently model fiber failure process during tensile loading, the fiber characteristic strength is determined by substituting mfand experimental tensile strength into Eq.(18),andec=1.768 GPa.
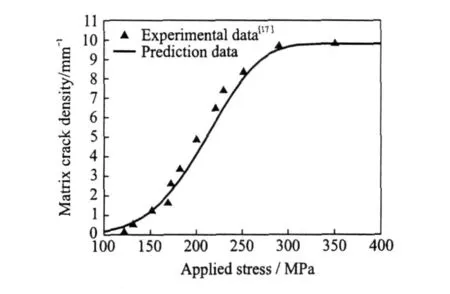
Fig.2 Matrix crack density versus stress of experimental measurement and theoretical prediction
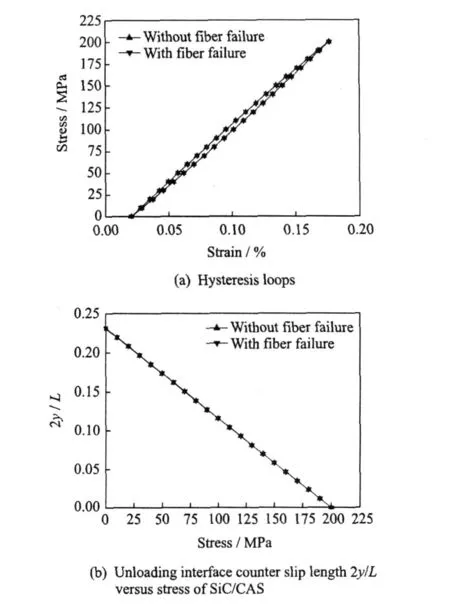
Fig.3 Effect of fiber failure whenemax=200 M Pa
The hysteresis loops with and without consideration of fiber failure whenemax=200 M Pa are illustrated in Fig.3(a).At this maximum unloading stress, the fiber/matrix interface partially debonds,2Ldf/L=0.47,and the fiber failure volume fraction is low,P(T)=0.38%.The unloading interface counter slip length y increases as stress decreases until emin,at which the counter slip length y does not approach the interface debonding tip,2y(emin)/L=0.23(Fig.3(b)).As the fiber failure volume fraction is low and the completely unloading interface counter slip length accounts for a small proportion of matrix crack space,the hysteresis loops of the two cases mentioned above are close with each other(Fig.3 (a)).

Fig.4 Effect of fiber failure whenemax=450 M Pa
The hysteresis loops with and without consideration of fiber failure whenemax=450 MPa are illustrated in Fig.4(a).At this maximum unloading stress,the fiber/matrix interface completely debonds,and the fiber failure volume fraction is 28.4%. The completely unloading interface counter slip length with consideration of fiber failure reaches interface debonding tip at the unloading stress which is larger than the minimum stress,2y(e>emin)/L=1,however,the counter slip length without consideration of fiber failure reaches interface debonded tip at the minimum stress,2y(e=emin)/L=1(Fig.4(a)).The shape, area and location of the hysteresis loops with consideration of fiber failure are different from those without consideration of fiber failure.When the effects of fiber failure on hysteresis loops are considered,the strains at the maximum and minimum stress,and the area of the hysteresis loops are all increased(Fig.4(b)).
The effects of fiber characteristic strength on the hysteresis loops and the unloading interface counter slip length whenemax=450 MPa are illustrated in Fig.5.The fiber failure volume fraction is 28.4% when ec=1.768 GPa,while the fiber failure volume fraction is 11% when ec=2.000 GPa.The increase of fiber failure volume fractions whenec=1.768 GPa makes the load carried by the intact fibers increase,which increases the unloading interface counter slip length y,the strains at the maximum and minimum stress and the area of the hysteresis loops.

Fig.5 Effect of fiber characteristic strength
The effects of fiber Weibull modulus on the hysteresis loops and the unloading interface counter slip length are illustrated in Fig.6.The fiber failure volume fraction is 28.4% when mf= 3.6,while the fiber failure volume fraction is 21.8% when mf= 4.The increase of fiber failurevolume fractions makes the load carried by the intact fibers increase,which increases the unload-ing interface counter slip length,the strains at the maximum and minimum stress and the area of the hysteresis loops.
5 EXPERIMENT COMPARISONS
Pryce and Smith[19]investigated the quasistatic unloading/reloading behavior of unidirectional SiC/CAS at room temperature.The hysteresis loops of the experimental data and the present analysis which considers the effect of fiber failure when emax=170,185,195 and 210 M Pa are shown in Fig.7.The material properties of SiC/CAS are given in Table 1.It is found that the hysteresis loops predicted by the present analysis agree well with the experimental data,which proves the efficiency of the present model.
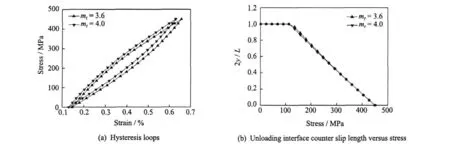
Fig.6 Effect of fiber Weibull modulus

Fig.7 Quasi-static unloading/reloading hysteresis loops

Table 1 Material properties of SiC/CAS ceramic matrix composites[19]
6 CONCLUSIONS
The effect of fiber failure on hysteresis loops under quasi-static unloading and subsequent reloading is investigated in the paper.As increasing the applied stress,the matrix crack space decreases,interface debonded length increases and the fiber failure volume fraction increases.The effect of fiber failure on hysteresis loops becomes obviously with the increase of the applied stress. The shape,area and location of hysteresis loops with consideration of fiber failure are different from those without consideration of fiber failure. The strains at the maximum and minimum stress of hysteresis loops,the area of the hysteresis loops all increase when fiber failure are taken into account.
When the unloading stress is constant,the fiber failure volume fraction and hysteresis loops as a function of fiber characteristic strength are analyzed.It is found that the fiber failure probability decreases with an increase of fiber characteristic strength and the strains at the maximum and minimum stress,and the area of the hysteresis loops decreases with an increase of fiber characteristic strength.
When the unloading stress is constant,the fiber failure volume fraction and hysteresis loops as a function of fiber Weibull modulus are analyzed.It is found that the fiber failure probability decreases with an increase of fiber Weibull modulus and the strains at the maximum and minimum stress,and the area of the hysteresis loops decreases with an increase of fiber Weibull modulus.
[1] Naslain R.Design,preparation and properties of non-oxide CMCs for applicationin engines and nuclear reactors:an overview[J].Composites Science and Technology,2004,64(2):155-170.
[2] Fantozzi G,Reynaud P.Mechanical hysteresis in ceramic matrix composites[J].Materials Science and Engineering,Part A: Structural Materials,2009, 521/522(15):18-23.
[3] Mei H,Cheng L F.Comparison of the mechanical hysteresis of carbon/ceramic-matrix composites with different fiber preforms[J].Carbon,2009,47(4): 1034-1042.
[4] Li Longbiao,Song Yingdong,Sun Zhigang.Influence of interface de-bonding on the fatigue hysteresis loops of ceramic matrixcomposites[J].Chinese Journal of Solids and Mechanics,2009,30(1):8-14. (in Chinese)
[5] Li Longbiao,Song Yingdong,Sun Zhigang.Effect of fiberPoisson contraction on fatigue hysteresis loops of ceramic matrix composites[J].Journal of Nanjing University of Aeronautics and Astronautics, 2009,41(2):181-186.(in Chinese)
[6] Li Longbiao,Song Yingdong.An approach to estimate interface shear stress of ceramic matrix composites from hysteresis loops[J].Applied Composite Materials,2010,17(3):309-328.
[7] Li Longbiao,SongYingdong.Estimate interface frictional coefficient of ceramic matrix composites from hysteresis loops [EB/OL]. http://jcm. sagepub.com/content/early/2010/10/20/002199831 0381437.abstract,2010-10-27/2011-03.
[8] Li Longbiao,Song Yingdong.Influence of fiber failure on fatigue hysteresis loops of ceramic matrix composites[J].Journal of Reinforced Plastics and Composites,2011,30(1):12-25.
[9] Kun F,Herrmann H J.Damage development under gradual loading of composites[J].Journal of Materials Science,2000,35(18):4685-4693.
[10]Yang B,Mall S.Cohesive-shear-lag model for cycling stress-strain behavior of unidirectional ceramic matrix composites[J].International Journal of Damage Mechanics,2003,12(1):45-64.
[11]Budiansky B,Hutchinson J W,Evans A G.Matrix fracture in fiber-reinforced ceramics[J].Journal of Mechanics Physics and Solids,1986,34(2):167-189.
[12]Curtin W A.Multiple matrix cracking in brittle matrix composites[J].Acta Metallurgica et Materialia, 1993,41(5):1369-1377.
[13]Sun Y J,Singh R N.The generation of multiple matrix cracking and fiber-matrix interfacial debonding in a glass composite[J].Acta Mater,1998,46(5): 1657-1667.
[14]Gao Y,Mai Y,Cotterell B.Fracture of fiber-reinforced materials[J].Journal of Applied Mathematics and Physics(ZAM P),1988,39(4):550-572.
[15]Curtin W A,Ahn B K,Takeda N.Modeling brittle and tough stress-strain behavior in unidirectional ceramic matrix composites[J].Acta Mater,1998,46 (10):3409-3420.
[16]Phoenix S L,Raj R.Scalings in fracture probabilities for a brittle matrix fiber composite[J].Acta Metallurgica et Materialia,1992,40(11):2813-2828.
[17]Beyerle D S,Spearing S M,Zok F W,et al.Damage and failure in unidirectional ceramic matrix composites[J]. Journal of the American Ceramic Society,1992,75(10):2719-2725.
[18]Aveston J,Cooper G A,Kelly A.Single and multiple fracture[C]//Properties of Fiber Composites: Conference on Proceedings. England: National Physical Laboratory,IPC,1971:15-26.
[19]Pryce A W,Smith P A.Matrix cracking in unidirectional ceramic matrix composites under quasi-static and cyclic loading[J].Acta Metallurgica et Materialia,1993,41(4):1269-1281.
 Transactions of Nanjing University of Aeronautics and Astronautics2011年1期
Transactions of Nanjing University of Aeronautics and Astronautics2011年1期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- 拉压、扭转载荷下铸铝合金的亿周疲劳性能研究
- 端墙形状对蒸汽涡轮效率的影响
- 法国MBDA爆震和连续爆震波发动机的研发
- 使用液态化学循环的高热效率动力研究
- FATIGUE LIFE PREDICTION METHOD FOR IMPACTED LAMINATES
- EXPERIMENTAL STUDY OF FORCED SHOCK TRAIN OSCILLATION IN ISOLATOR UNDER ASYMMETRIC INCOMING FLOW
