迭代计算方法在测绘领域中的具体应用

王建国

(中煤国际工程集团南京设计研究院，江苏南京 210031)

迭代计算方法在测绘领域中的具体应用

王建国∗

(中煤国际工程集团南京设计研究院，江苏南京 210031)

应用迭代计算方法总结出计算点位到特殊曲线径向距离的算法，并根据算法原理编制相应程序，实践应用证明程序的正确性、可靠性和实用性。

迭代；算法；径向距离

1 引 言

迭代法是一种不断用变量的旧值递推新值直到误差小于事先设定的容许误差完成迭代计算的过程。迭代法作为一种很常用也很重要的计算方法在测绘诸多领域中均有应用，如:监测网优化设计规划求解、卡尔曼滤波五组核心递推公式、BP神经网络训练、空间直角坐标反算大地坐标、赫尔默特方差分量估计、道路点位坐标反算施工坐标、拱坝溢流坝计算点位径向距离等。

本文主要对点位到特殊曲线的径向距离展开讨论，并以工程实例进行验证。

2 原理推导

现在要计算点P(X0，Y0)到曲线的径向距离、径向方向线和曲线交点的高程以及该交点距原点的弧长。解决这个问题的关键在于如何找到计算点P对应于曲线上的某一点Q。为了寻找这样的点，思路有三:

(1)以计算点P为圆心的圆与特殊曲线刚好相切所对应的切点即为Q点。

(2)过曲线上点Q的切线的斜率K1与Q点和P点的连线的斜率K2有这样的数学关系，即:K1×K2＝0，该方程为仅含有未知数X的一元方程。解算最终可得Q点坐标X、Y值。

(3)使得过曲线上Q点的法线恰好通过计算点P。

本文即是基于第三种思路运用迭代的算法来寻找满足要求的Q点。

目前点到缓和曲线的最短距离讨论的文献资料也较多。文献[1]用点P到通过迭代点的法线之垂距作为里程迭代增量，直到垂距小于设定的精度要求，迭代收敛。文献[2]用点P与迭代点的距离、迭代点处的切线、点P到切线的垂线构造直角三角形，用切线长作为里程迭代增量，直到迭代点的切线与点P的切线重合，迭代收敛。本文结合上述两文献的迭代思想来解决点到曲线的最短距离问题。

首先建立如图1所示的坐标系。我们假定曲线上任一点P1(X1，Y1)，则过点P1的法线为P1A，计算点P到法线P1A的距离DPA，可得知P点相对于法线的位置(P点在法线P1A左侧时PA为负，在右侧时PA为正，相对于图上而言)，通过该相对位置使法线向点P移动，移动所需的X坐标的改变量△X≈DPA×cos(α)。通过这样修正该点的X坐标使法线向点P移动，当移动满足点P到法线的距离小于所设定的精度时迭代结束，曲线上该点便是点P对应于曲线上某一点的近似点(如图1中的B点)，上述过程可简述为如下步骤:

①计算过假定点P1(X1，Y1)的法线的坐标方位角F；

②计算点P(X0，Y0)到法线P1A的垂直距离DPA；

③对假定点P1的坐标X1进行修正:

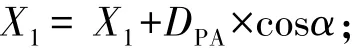
④DPA值大于所设定的精度则重复上述步骤，否则迭代结束；

某曲线设其方程为:

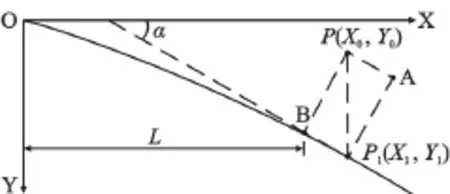
图1 工程坐标系中点与曲线关系原理图

对式(1)求导数得:

上述式(2)一阶导数可理解为过曲线上某点的切线的斜率K即:

因此，切线坐标方位角:

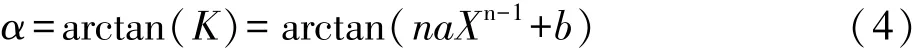
则通过直线P1A的坐标方位角为:

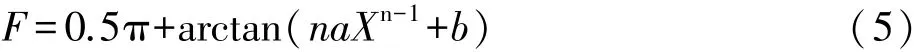
而直线P1P的坐标方位角αP1P可以通过这两点坐标反算求得，则点P到直线P1A的距离:

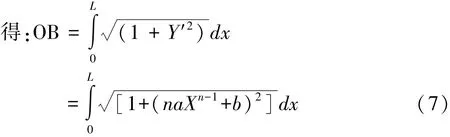
上式中L为交点B的横坐标。

3 工程实例

某工程纵剖面图如图2，其设计线形曲线方程为:Y＝X2/400＋0.023X。本文应用上面介绍的原理编制相应的程序，计算结果如表1所示。

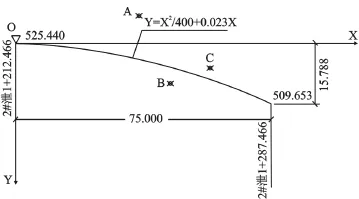
图2 隧道龙落尾纵剖面图

图2 中三点坐标:A(36.3215，532.7096)、B (45.5541，514.8421)、C(57.1535，519.0177)分别位于曲线的典型位置，计算结果如表1所示。

迭代解法与直接解法计算结果比较表(单位/m) 表1

迭代程序部分主要代码如下:

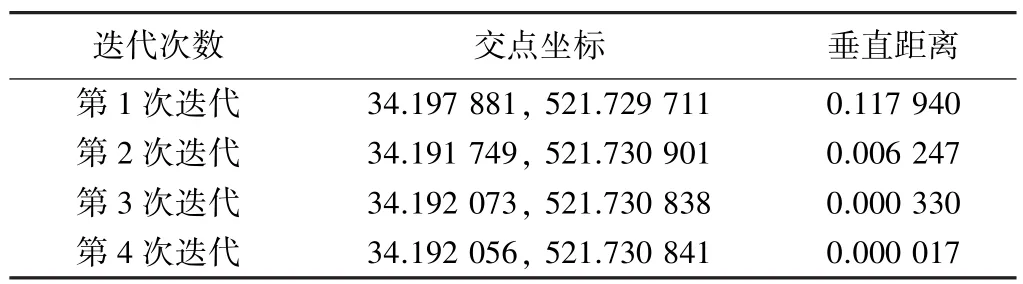
迭代解法计算过程表(单位/m) 表2

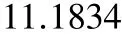
从以上实例可以看出:

(1)计算的结果正确，迭代次数在工作中可以接受；实际工作中可通过调整迭代精度控制计算速度。

(2)计算精度可控，由于计算出了移动所需的大致X坐标差来进行修正，计算出交点的X坐标值的误差约为限定的计算精度和该点切线角的余弦之积。

4 结 语

思路一效率较低，实际工作中不建议采用，思路二、三在实际工作中可以采用，结合一种计算机语言如Matlab或VB编程能够批量自动计算，从而使工作效率得以提高。

本文探讨了点位到一类曲线的径向距离的一种迭代算法，简要分析了算法的速度和计算的精度。实例验证该算法原理正确，通用性强，程序易于实现，能够满足实际工作的需要。

[1] 李全信.确定地面点与线路中线相对关系的统一数学模型[J].测绘通报，2002(8)

[2] 冯晓，李敏.任意组合曲线坐标正反算通用算法及应用试验[J].矿山测量，2008(2)

[3] 任玉杰.数值分析及其MATLAB实现[M].北京:高等教育出版社，2007

[4] 佟士懋，邢芳芳，夏齐霄.AutoCAD ActiveX/VBA二次开发技术基础及应用实例[M].北京:国防工业出版社，2006

The Specific Application of Iteration in Surveying and Mapping

Wang JianGuo
(Sino Coal International Engineering Group Nanjing Design Institute，Nanjing 210031，China)

In this paper，the algorithm of calculating radial distance between points and curve by using iteration is introduced.Based on the algorithm，writer design relevant programme.The result shows that it is accurate，reliable and practical.

iteration；algorithm；radial distance

1672－8262(2011)02－153－03

P209

B

2010—08—10

王建国(1980—)，男，工程师，主要从事工程测量及数据处理研究。