利用Matlab进行变形监测数据回归分析的探讨

王磊，陈伟清，胡加星

(1.桂林理工大学土木工程系，广西桂林 541004； 2.广西大学土木建筑工程学院，广西南宁 5300041)

利用Matlab进行变形监测数据回归分析的探讨

王磊1∗，陈伟清2，胡加星1

(1.桂林理工大学土木工程系，广西桂林 541004； 2.广西大学土木建筑工程学院，广西南宁 5300041)

通过运用Matlab软件对实测沉降观测数据建立回归分析模型，并通过该模型对未来的沉降值进行预测，达到了预期的效果。证实了该方法在变形观测数据处理方面的可行性。

回归分析；Matlab；预测变形；拟合曲线

1 引 言

回归分析方法在工程建筑物的变形分析中可用于建立位移量与某些相关因素(如时间、荷载等)之间的数学关系，即建立回归方程。根据相应的回归方程分析变形的某些现象，并预报位移量，从而起到对灾害的预警作用。Matlab是一套高性能的数值计算和可视化软件，是实现数据分析与处理的有效工具。本文使用Matlab方便快捷地对监测数据建立回归分析模型，并通过该模型预测未来变形值，取得了很好的预测精度。

2 多元回归分析模型

研究一个随机变量与一个(或几个)可控变量之间的相关关系的统计方法称为回归分析。只有一个自变量的回归分析叫做一元回归分析，多于一个自变量的回归分析叫做多元回归分析。在进行对引起变形的原因做出分析和解释时，通常建立荷载、时间等因素与变形关系的数学模型，这就需要用到多元回归分析模型。

2.1 多元回归分析模型的建立

设y是一个可观测的随机变量，它受到m－1个非随机因素x1，x2，…，xm－1和随机因素ε的影响。若y与各因素间有如下线性关系:

式(1)中，β0，β1，…，βm－1是未知参数，ε～N(0，σ2)。该模型称为多元线性回归模型。

2.2 模型参数的确定

为了估计β0，β1，…，βm－1，应进行n(n≥p)次独立观测，得到n组数据(称为样本)。式(1)可用矩阵表示为:

其中:Y＝[y1y2…yn]T

2.3 模型统计推断

(1)回归关系的统计推断

为检验y与x1，x2，...，xm－1之间是否存在显著的线性回归关系，即检验假设:

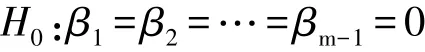
式(3)中，SR表示回归值与均值的离差，这是由回归所能解释的部分；Se表示观测值yi与回归值的离差，即残差ei，这是不能由回归加以解释的部分；ST为yi与的离差。记S被称为剩余标准差，用它来表示回归方程的精度。

(3)偏回归系数检验

回归关系显著并不意味着每个自变量xi(1≤i≤m－1)对y的影响都显著，可能其中的某个或某些对y的影响不显著。为此就需要对每一个回归系数作显著性检验来剔除对y的影响不显著的自变量。即检验假设:

3 利用Matlab进行变形监测数据回归分析

在运用Matlab进行回归分析时，可以通过编写M文件的方式进行处理，这样不但可以得到模型参数，还可以对模型进行相应的统计推断。按照上述公式即可编辑用于进行多元回归分析的M文件。

沉降点CJ1数据 表1

表1为南宁市民生广场沉降观测点CJ1数据，其中包括时间间隔、荷载和累计沉降量。

取前15期数据进行回归模型的建立，后5期的数据用来与回归模型预测得数据相比较，以检验预测的准确性。

3.1 回归模型的建立及相应的统计推断

记X1为时间向量，X2为荷载，Y为累计沉降量。在M文件中可直接输入已知数据，由于模型中有常数项，因此X1，X2按照X＝[1X1X2]的形式输入，第一列全为1。Y的输入方式不变。M文件的代码如下:

方差分析表 表2

相关系数R＝0.970 13

剩余标准差S＝0.181 28

因素的显著性为[显著；显著]

相关系数R接近1，说明回归方程和数据点的拟合度很高。

由运行结果知，Y与X1，X2的存在着显著的线性回归关系，X1，X2对Y的影响也是显著的，因此以

作为回归方程。

3.2 沉降预测及分析

根据回归方程就可以对后5期沉降值作出预测，预测结果如表3所示。

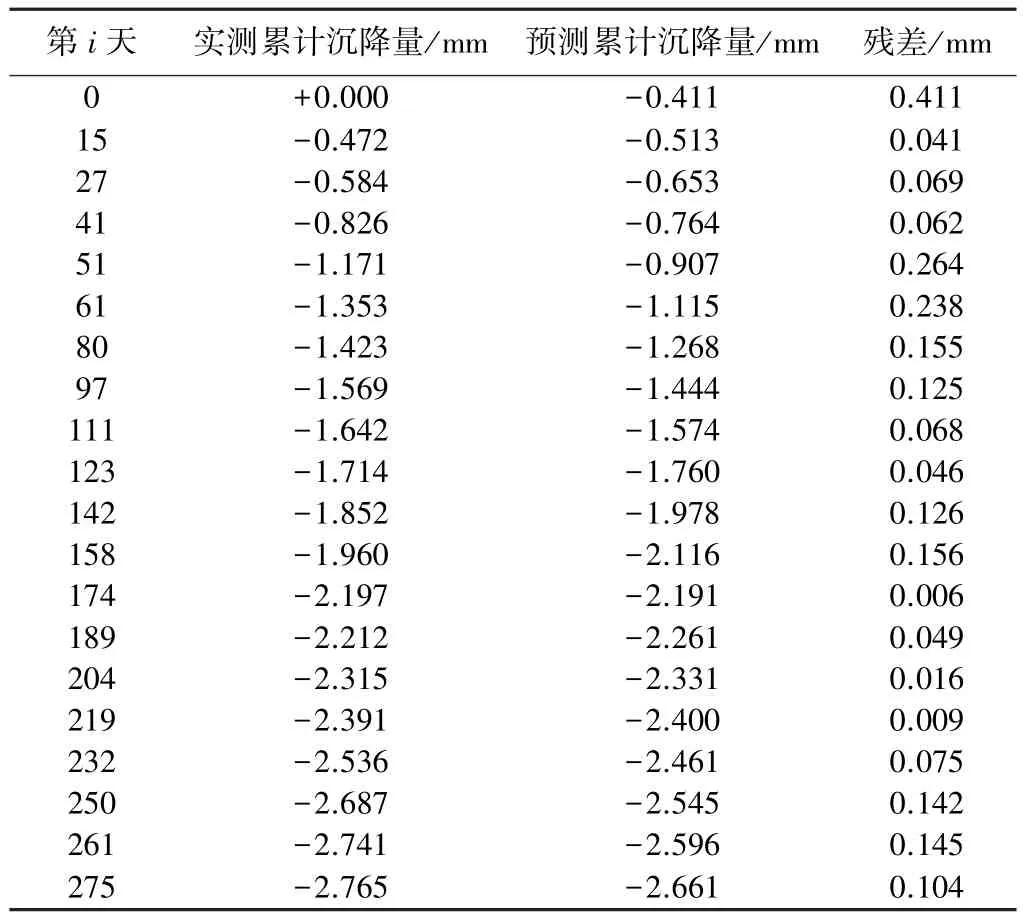
预测下沉值和残差值 表3

由表3和图1可看出，第16、20期的预测结果与实测结果最为接近，第17、18、19期的预测结果与实测结果有一定差异，但都小于预测中误差(剩余标准差S)。最后5期的实测结果和预测结果都表明，沉降速度均不超过0.04 mm/d。因此，可认为沉降预测值是比较可靠的。

图1 CJ1点沉降实测曲线和预测曲线图

4 结 语

通过上例可以看出，运用Matlab可以方便地对变形监测数据进行回归分析，并对今后的变形趋势进行预测，从而对变形体起到预警作用。但在进行回归分析时要注意以下几点:

(1)进行回归分析时要充分考虑和变形值有关的因素，剔除对变形值影响小的因素，这样预测出的变形值才更可靠。本文不仅考虑了时间对变形的影响，还考虑了荷载的因素，因此得到的预测结果才比较准确。

(2)回归分析模型的一个缺点是建立该模型进行变形值的预测需要有大量先前观测值，如先前观测值太少，拟合效果就越差，拟合结果甚至是错误的，这样的回归分析模型是没有意义的。而在用Matlab进行建模时，不论什么样的原始数据，都会得到回归模型参数，如果不对回归参数进行假设检验，回归分析模型也是没有意义的。

(3)在实际工作中，拟合只能是对已有数据的逼近，不可能对事物的全过程给出完整的描述。根据局部的或是有限的数据资料建立模型，只能适合于局部的或近期的预测。预测愈远，误差愈大，这是由于出现误差累积的结果。因此，预测超前期一般由实际情况而定。

[1] 栾元重，吕法奎，班训海等.动态变形观测与预报[M].北京:中国农业科学技术出版社，2007，95～116

[2] 王岩，隋思涟，王爱青.数理统计与MATLAB工程数据分析[M].北京:清华大学出版社，2006，161～172

[3] 岳建平，田林亚.变形监测技术与应用[M].北京:国防工业出版社，2007，121～125

[4] 陈伟清.回归分析在建筑物沉降变形分析中的应用[J].测绘学院学报，2005，22(4):250～251

[5] 张俊中，宋蕾，张健雄.多元回归分析模型在变形监测中的应用[J].河南工程学院学报(自然科学版)，2009，21 (3):22～25

[6] 叶斌，鲍峰.考虑建筑物荷载的变形监测数据处理方法[J].四川测绘，2006，29(2):60～63

[7] 邹利.回归分析在大坝变形监测数据处理中的应用研究[J].工程地球物理学报，2007，4(6):644～647

[8] 郑萧，金青.回归模型与时间序列在大坝变形监测中的应用[J].湖北师范学院学报(自然科学版)，2010，30(1): 83～88

The Inquiring about Regression Analysis of Deformation Data by Matlab

Wang Lei1，Chen WeiQing2，Hu JiaXing1
(1.College of Civil and Architectural Engineering，Guilin University of Technology，Guilin 541004，China；2.College of Civil and Architectural Engineering，Guangxi University，Nanning 530004，China)

This paper applies the model of regression analysis in survied deformation data of settlement by Matlab and uses the model to forecast the settlement in the future.The result of the forecast is approach to the result of survied deformation data in the future.

the function of experience regression；Matlab；settlement forecast；fitted curve

1672－8262(2011)02－136－03

P209

A

2010—08—25

王磊(1984－)，男，硕士研究生，助理工程师，主要研究方向:变形监测数据处理。

广西自然科学基金项目(2010GXNSFA013002)；广西教育厅科研项目(200808MS148)