基于小波变换对GPS信号去噪的分析

屈利娜，许本意

(桂林理工大学土木与建筑工程学院，广西桂林 541004)

基于小波变换对GPS信号去噪的分析

屈利娜∗，许本意

(桂林理工大学土木与建筑工程学院，广西桂林 541004)

小波分解能够精细地把信号划分到不同的频带范围内，因此可对含噪信号在不同频带范围内的特征进行信噪分离。本文从GPS精密测量、导航领域的信号去噪角度，探讨了基于小波分析的信噪分离方法，并结合具体实例，说明小波分析对GPS信号消噪处理的实用性及有效性。

小波变换；多分辨率分析；GPS信号；信噪分离

1 引 言

小波(Wavelet)被人们称为“数学显微镜”。与Fourier变换相比，主要的区别是小波在时域和频域都是局部的。而标准的傅立叶变换只在频域上是局部的。小波变换是空间(时间)和频率的局部变换，因而能有效地从信号中提取信息。通过伸缩和平移等运算功能可对函数或信号进行多尺度的细化分析，解决了Fourier变换不能解决的许多困难问题，成为继Fourier变换以来在科学方法上的重大突破。本文主要讨论应用小波分析的理论，利用Matlab软件在计算机上实现了GPS信号的噪声消除，从混有噪声的实际GPS信号中提取了原始信号，在GPS测量、导航领域具有非常实用的意义。

2 问题描述

GPS信号在生成和传播的过程中，常常会受到很多噪声的干扰而使得质量变差，因此，有目的地从GPS测量数据中获取有用的信息，即对GPS信号去噪，是对GPS信号分析一个十分重要的步骤。

如上所述，设f(t)是已经被污染的GPS信号，即带有噪声的信号，则数学模型可以写为:

3 小波分析

3.1 离散小波变换

在连续小波变换中，我们考虑:

这里b∈R，a∈R，a≠0，ψ满足容许条件。为了方便起见，仅考虑a为正数的情况，这时，容许条件就变为:

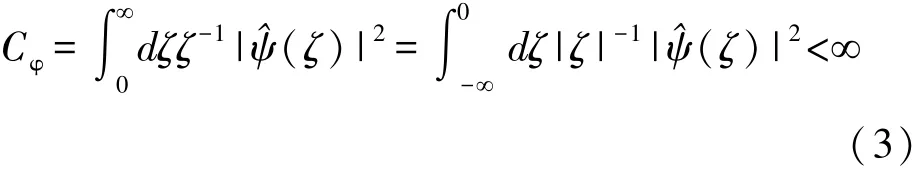
我们限制a，b为离散值的情形。对于离散化的固定伸缩步长，我们可以选及a0≠1均是确定的。不失其一般性可以假定a0>1(这是可以的，因为m可取正亦可取负)。在m＝0，可很自然地离散化b为某个b0的整数倍(b0是任意确定的正数)，b0经适当选取以使ψ(x－nb0)覆盖整个实轴。对不同的m，的宽度是ψ(x)宽度的am0倍(比如以宽(f)来度量，这里假定的选择确保了离散小波在m水平上与ψ(x－nb0)同样地覆盖了整条实轴。因此，我们取其中m，n取遍Z，a0>1，b0>0是确定的；当然a0，b0的选择依赖于ψ。于是有:

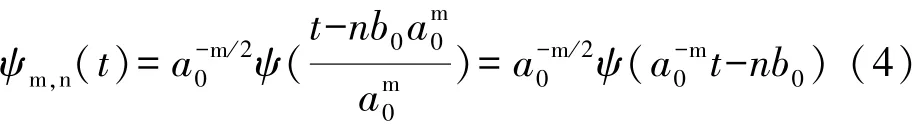
3.2 多尺度分析

多尺度分析也称多分辨率分析(MRA)，MRA是指L2(R)中的一列闭子空间，满足一定的条件。该定义中给出的是尺度函数或父函数φ(t)(和母函数相对)。设L2(R)的一个闭子空间的嵌套序列{Vk}，k∈Z，即:

如果满足以下条件:

(1)一致单调性:Vj⊂Vj－1；

直到无法满足总时间约束由此可以确定小车移动过程中各停留点的停留充电时间，同时规避了节点剩余能量小于能量阈值的情况.

(2)平移不变性:u(x)∈Vj⇔u(x－k)∈Vj；

其中，Vm是低通滤波器，Wm是高通滤波器，Vm和Wm由Vm＋1空间上的信号分解得到，以此类推，Vm还可以进一步分解，直到满足要求为止。

4 小波分析去噪方法

利用swt函数对含有噪声的GPS信号进行分解，然后使用iswt函数对GPS信号进行重构。设置固定伸缩参数，用尺度函数对已知输入的GPS信号不断地进行分解和重构，直到满足要求为止。

4.1 单尺度一维离散平稳小波分解

利用Matlab中如下程序实现:[swa，swd]＝swt(s，1，’db1’)。结果如图1所示。

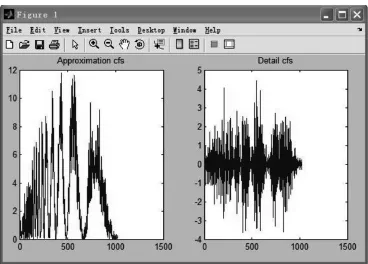
图1 一维离散平稳分解后的低频和高频部分

4.2 平稳小波逆变换重构信号并构建低频和高频部分

利用Matlab中如下程序实现:A0＝iswt(swa，swd，’db1’)；err＝norm(s－A0)；nulcfs＝zeros(size (swa))。结果如图2所示。

4.3 多层平稳小波分解

利用Matlab中如下程序实现:[swa，swd]＝swt(s，3，’db1’)；结果如图3所示。

4.4 利用重构的不同层高、低频信号重构所需层低频信号

利用Matlab中如下程序实现:mzero＝zeros(size (swd))；

A(3，:)＝iswt(swa，mzero，’db1’)；A(2，:)＝A (3，:)＋D(3，:)；。结果如图4所示。

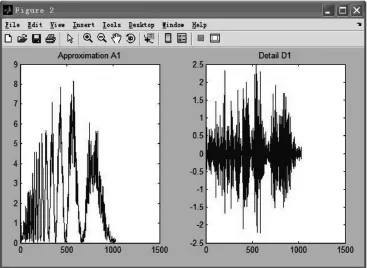
图2 重构后的低频和高频部分

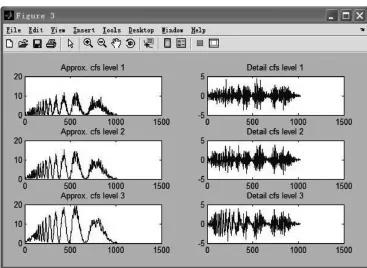
图3 多层平稳分解后的低频和高频部分

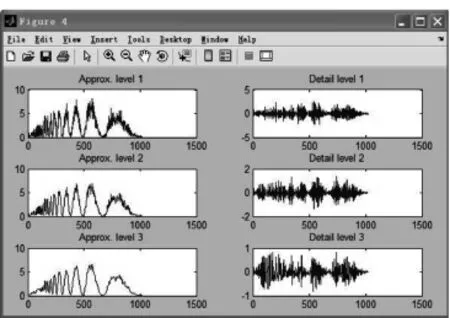
图4 多层重构后的低频和高频部分

4.5 去除信号中的噪声

利用Matlab中如下程序实现:[thr，sorh]＝ddencmp(’den’，’wv’，s)。结果如图5所示。

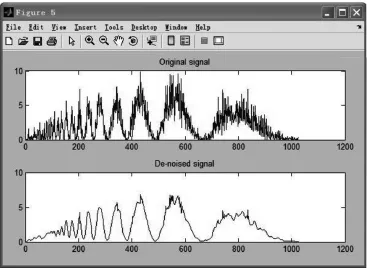
图5 原始信号和去噪后的信号

4.6 对信号进行五层次的分解并重构以消噪

利用Matlab中如下程序实现:[swa，swd]＝swt(s，5，’db1’)；[thr，sorh]＝ddencmp(’den’，’wv’，s)；结果如图6所示。

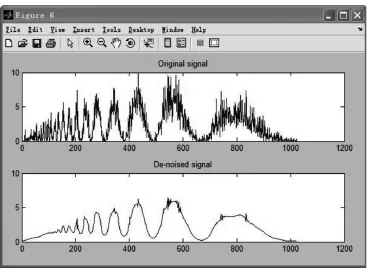
图6 原始信号和多层重复去噪后的信号

5 结 语

小波变换是一种信号的时频分析方法，它具有多分辨率分析的特点，利用小波多分辨率分析，可以很好地保存有用信号中的尖峰和突变部分。能够将有用信号的高频部分和由噪声引起的高频干扰予以有效地区分。因此，小波分析对非平稳信号的消噪，有着傅立叶分析不可比拟的优点。通过Matlab编程利用小波工具箱进行GPS信号的噪声消除的实验表明:小波理论的迅速发展，及其具备良好的时频特征，使得利用小波变换进行GPS信号分解及重构以达到去噪效果具有十分广阔的前景和实用价值。

但是，在实际操作中，用小波分析存在这样一个问题，由于受到多种因素的干扰，从当前级选取的极值点跳到下一级选取极值点时，有时不止一个极值点，有时却找不到极值点。如果要用Matlab程序实现信号频域由低频到高频的自动跟踪，以达到自适应学习进而把握尺度函数，往往不是很容易的。因此，需要我们通过不断的具体调试，总结出一些经验性的可靠判据，才能收到较好的效果，以达到解决问题的目的。

[1] 程正兴，杨守志，冯晓霞.小波分析的理论、算法、进展和应用[M].北京:国防工业出版社，2007:72，79～80，304～313

[2] Boggess，A.，苪国胜(译).小波与傅里叶分析基础[M].北京:电子工业出版社，2004:170～205

[3] 石为人，罗雪松，胡宁.基于小波多分辨率分析的信号消噪[J].重庆大学学报(自然科学版)，2002(6):59～62

[4] 石双忠.基于小波技术的时序分析法用于GPS监测数据处理的研究[D].南京:河海大学，2004:19～40，42～61

[5] 邹鲲，袁俊泉，龚享铱.MATLAB 6.x信号处理[M].北京:清华大学出版社，2002:83～114

[6] MALLAT S.A theory for multiresolution signal decomposition，the wavelet representation[J].IEEETrans，1989 On PAMI－11(7):674～693

GPS Signal De－noising Analysis Based on the Wavelet Transform

Qu LiNa，Xu BenYi
(Civil Eengineering College of Guilin University of Technolocy，Guilin 541004，China)

Wavelet decomposition can be divided into the signal in different frequency band range，so it can do signal－to－noise separation characteristics to noise signal in different frequency range.From the GPS navigation field precision measurement，denoising Angle，it was discussed the method of signal－to－noise based on wavelet analysis.Combined with a specific examples，it explain the wavelet analysis of GPS signal de－noising practical and effective treatment.

Wavelet transform；Multiresolution analysis；GPS signal；The SNR separation

1672－8262(2011)02－65－03

P228

A

2010—10—20

屈利娜(1985—)，女，硕士研究生，主要研究GPS高精度数据处理与应用。

广西研究生教育创新计划资助项目(2010105960816M37)