GM(1,1)模型在建筑物沉降预测中的应用及Matlab的实现
陈刚,王波,邓哲
(江西理工大学建筑与测绘工程学院,江西赣州 341000)
GM(1,1)模型在建筑物沉降预测中的应用及Matlab的实现
陈刚∗,王波,邓哲
(江西理工大学建筑与测绘工程学院,江西赣州 341000)
针对建筑物出现的变形问题,提出在现有建筑物观测数据的基础上,运用灰色理论的方法,建立GM(1,1)模型,来预测该建筑物的沉降量,并用Matlab来对GM(1,1)算法进行实现。分析结果表明,GM(1,1)模型能较好地预测建筑物的沉降发展趋势,具有较强的实用性。
灰色理论;GM(1,1)模型;Matlab;预测
1 前 言
随着我国经济的飞速发展,高层建筑物越来越多。许多建筑物,特别是高层建筑在施工和运营期间,由于受多种因素的影响,会产生变形,变形如果超出了规定的限度,就会影响建筑物的正常使用,严重时还会危及建筑物的安全,给社会和人民生活带来巨大的损失。因此,采用科学的方法对建筑物进行沉降观测,对其未来的变形趋势做出准确的预测,具有重要的意义。
灰色系统理论主要研究“小样本不确定问题”,在贫信息少数据的情况下有着其独到的优势。Matlab是集数学计算、图形处理和程序语言设计于一体的著名数学软件。在Matlab语言系统中,几乎所有的操作都是以矩阵操作为基础,而在GM(1,1)模型的灰色预测过程中,需要进行大量的矩阵运算,Matlab在这方面显示了独到之处。将Matlab和GM(1,1)模型结合,实现灰色预测算法,提高了计算的效率。本文从灰色理论出发,通过建立GM(1,1)模型并结合实测资料来对建筑物进行变形预测,利用Matlab来对其程序进行实现,充分验证了该模型的可行性和可靠性。
2 灰色预测模型介绍
灰色系统理论是20世纪80年代由我国邓聚龙教授提出,并用来解决信息不完备系统的复杂问题,它是一种数学方法.在实际解决问题时,通过选择适当的方式去挖掘已知部分的信息或数据,充分利用灰色理论中的相关方法来解决这些复杂问题。灰色预测模型主要是应用灰色系统理论,对所得的数据列建立动态模型。GM(1,l)是实际应用中最为普遍的一种灰色预测模型,是灰色系统理论的核心模型。该模型仅用4个数据就可以估计模型参数,且可达到一定的模拟精度。
灰色GM(l,l)模型建模的实质是对原始数据一次累加生成,使生成数据序列呈一定规律,通过建立一阶微分方程模型,求得拟合曲线,用以对系统进行预测。具体步骤如下:
第1步,作累加生成数列。对于数列作一次累加生成1-AGO,对于给定的原始时间序列,记作:
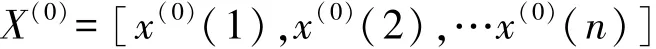
作累加得到:X(1)=[x(1)(1),x(1)(2),…x(1)(n)]
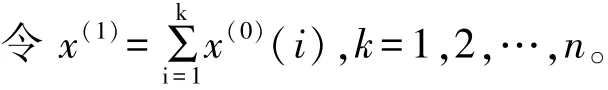
第2步,作X(1)(1)的紧邻均值生成系列:
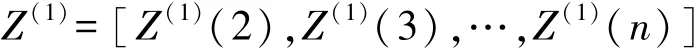
第3步,构造累加矩阵B和常数向量Y。

第4步,利用最小二乘法,通过Matlab拟合来求解灰参数a,b。
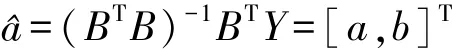
第5步,确定微分方程模型。

第6步,得到时间响应式。
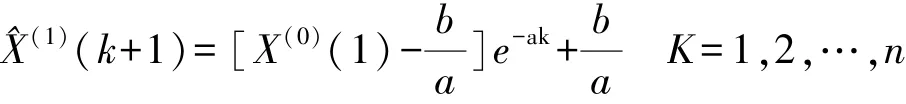

第8步,模型精度检验,
一般判断GM(1,1)模型的精度方法有三种,分别为:残差大小检验,关联度检验和后验差检验。本文采用的是后验差检验方法。模型精度由均方差比值和小误差概率共同评定。后验差方法一般是按后验差比值C和小误差概率P两个指标综合评定预测模型的精度。方法如下:
令x(0)(k)为实际值为预测值,则:

精度检验要求均方差比值C越小越好,C小表明尽管原始数据很离散,而模型所得计算值与实际值之差并不太离散。一个好的模型要求在S1大的前提下,S2尽可能小。一般要求C<0.35,最大不超过0.65。指标P越大越好,一般要求P>0.95,不得<0.70。
3 Matlab程序的实现


4 实例分析
本文所选为河南某小区北楼的监测点A1的监测数据来进行建模分析。其中观测数据以月为时间单位,并且是等时间间隔观测。本文以2007年1月~9月的沉降数据为样本值,预测10月和11月的沉降量,具体如表1所示。
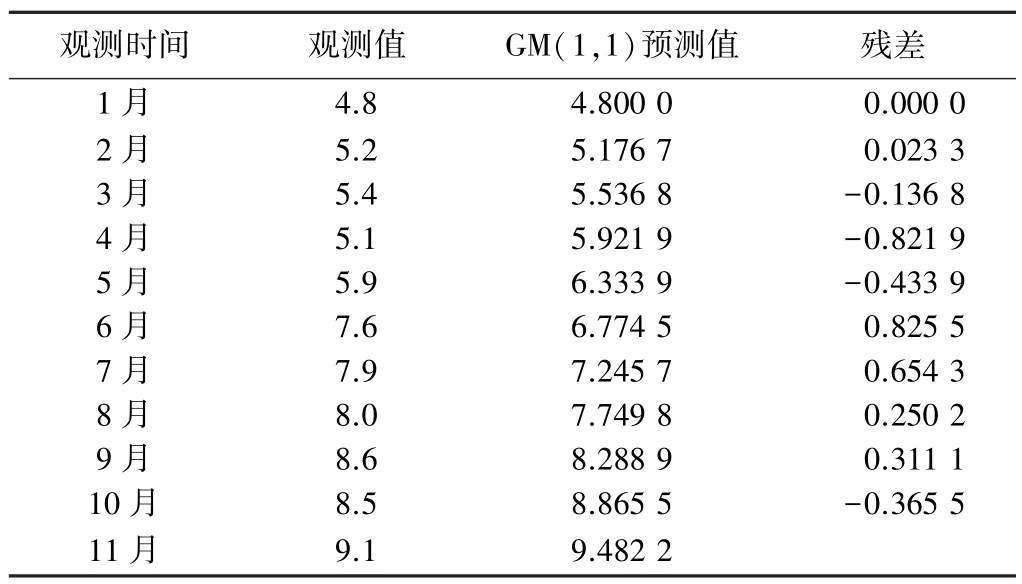
灰色预测模型的相关数据 表1
从表1中可以看出10月的预测值为8.865 5,而实际观测值为8.5。11月的预测值为9.482 2,而实际观测值为9.1。预测结果与实测数据非常吻合,并且通过Matlab程序,我们可以得出该GM(1,1)预测模型的后验差比值C=0.090 8,小误差概率P=1,预测精度为一级。这样就更进一步证实了灰色预测模型的拟合效果是令人满意的。
5 结 语
实例表明通过建立灰色理论模型预测建筑物的沉降变形,不但精度可靠,而且无需大量的观测数据便可建模,从而得到较为理想的预测结果,很好反映出了建筑物的沉降发展趋势。并且利用Matlab来实现灰色模型的算法,程序简洁,算法清楚,预测精度高,具有很强的实用性。
[1] 何芳.用灰色预测法预测河池市中期用水量[D].华中科技大学,2006
[2] 于国芳.地基变形的灰色预测模型[J].西部探矿工程,2009(2):11~14
[3] 习徐君.基于GM(1,1)模型的矿井瓦斯涌出量预测研究[J].矿业研究与开发,2005(3)
[4] 导向科技.Matlab 6.0程序设计与实例应用[M].北京:中国铁道出版社,2001
[5] 姚东,王爱民,冯峰等.Matlab命令大全[M].北京:人民邮电出版社,2000
The Application of GM(1,1)Model for Predicting the Building and Implementation of Matlab
Chen Gang,Wang Bo,Deng Zhe
(Jiangxi University of Architecture and Surveying Institute,Ganzhou 341000,China)
Aimed at the Deformation of the building,Proposed the method of using gray theory to build the gray mode on the basis of observation data of building to predict the settlement of the building,and Achieve GM(1,1)algorithm by using Matlab.The results show that GM(1,1)model has a strong practicalto predict the development trend of settlement building.
grey theory;GM(1,1)model;Matlab;prediction
1672-8262(2011)01-107-03
P209
B
2010—06—24
陈刚(1985—),男,在读研究生,主要研究方向是:数字城市技术与方法。

