变速控制力矩陀螺模式调度型操纵律设计*

杨雅萍，吴 忠

(北京航空航天大学仪器科学与光电工程学院，北京 100191)

单框架控制力矩陀螺(SGCMG)由恒速旋转的飞轮和支撑飞轮的框架组成，输出力矩大，但力矩分辨率较低，并存在奇异问题［1-2］.飞轮则是一种转速可变的姿态控制执行机构，输出力矩分辨率高，但力矩量值较小.为在航天器姿态控制系统中充分发挥SGCMG、飞轮各自的优点，可将SGCMG的恒速飞轮改为变速飞轮，即为变速控制力矩陀螺(VSCMG).在VSCMG中，通过框架转动可以输出较大的力矩，通过飞轮转速改变可以提高输出力矩的分辨率，并可以借助飞轮力矩回避奇异.正是由于VSCMG兼具控制力矩陀螺和飞轮的优点，不但可以实现航天器姿态的快速机动，而且可以实现航天器姿态的高精度高稳定度控制，必将引起航天控制领域的广泛关注［3-5］.

为利用VSCMG实现航天器姿态控制，必须为其设计性能良好的操纵律，把姿态控制需要的力矩指令分解为每一个VSCMG的框架和飞轮指令.对于VSCMG操纵律，文献［6］曾针对平行构型的VSCMG群，设计了奇异状态下仍然可控的操纵律;文献［7-8］则根据航天器的工作状况，在操纵律的设计中考虑了CMG模式和RW模式的切换;文献［9-10］则采用加权阵对CMG模式和RW模式进行力矩分配和调节，并加入梯度型零运动回避奇异;文献［11-12］则研究了两种转子转速均衡方法，可以避免飞轮转速过高或过低.

在以上操纵律研究中，大都将框架和飞轮运动所产生的力矩考虑在一起，并通过求解一个3×2N Jacobian阵的伪逆得到框架和飞轮指令，没有充分考虑框架和飞轮的特点.文献［13］则不同，将VSCMG的工作分解为CMG模式和RW模式.在陀螺群接近奇异时，启用RW模式来补偿单纯CMG模式下奇异鲁棒逆操纵律引起的力矩误差;在陀螺群远离奇异状态时，启用CMG模式来补偿转子储能带来的干扰力矩.实际上，在文献［13］中，框架及飞轮均处于控制状态，RW模式与CMG模式配合工作，应为典型的VSCMG模式.

本文从力矩分配的角度出发，设计一个模式自主调度的VSCMG操纵律.通过指令力矩方向与VSCMG力矩方向之间的关系，设计一个力矩分配方案，将姿态控制需要的力矩指令分解为CMG指令(框架转速指令)和RW指令(飞轮转速指令).当系统远离奇异时，仅以CMG模式工作，产生大的输出力矩.当系统接近奇异时，引入RW模式与CMG模式配合，以VSCMG模式工作，协助VSCMG回避奇异.当处于姿态稳定模式，需要提供精细的姿态控制力矩时，可采用单纯的RW模式工作.此操纵律把一个3×2N矩阵的求伪逆问题转化为两个3×N矩阵的求伪逆问题，物理意义明显，且易于回避奇异.

1 数学模型

假设在某刚体航天器上，安装N个VSCMG.定义gi、si分别为第i个VSCMG的框架角速度方向和转子转速方向的单位矢量，ti=gi×si为横向方向单位矢量，si、ti为框架角 γi的函数，i=1，…，N.三者的关系可以表示如下:

由于框架角速度远远小于飞轮的转速，在以下推导过程中，忽略框架角速度对系统角动量的影响.如果设Iwsi为第i个VSCMG的转子相对其转子轴的转动惯量，转子转速为Ωi，则其角动量大小为hi=IwsiΩi，角动量矢量可以表示为 hisi.因此，N 个VSCMG的总角动量可表示为

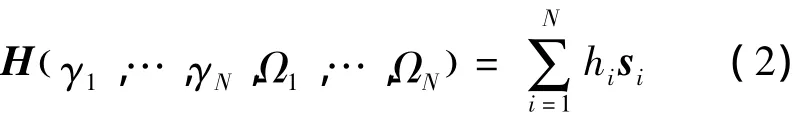
H相对于时间的导数即为航天器本体作用于VSCMG的力矩，这一力矩与VSCMG作用于航天器的力矩大小相等方向相反.即

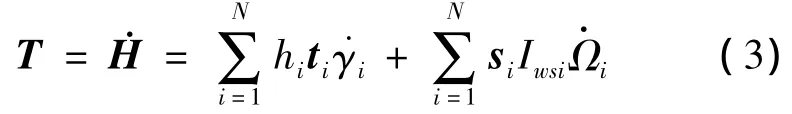
写成矩阵形式为

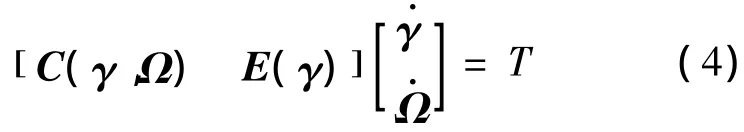
其中:C(γ，Ω)=［Iws1Ω1t1，…，IwsNΩNtN］ =AtIws［Ω］d;E(γ)=［Iws1s1，…，IwsNsN］=AsIws;C、E分别为CMG模式及RW模式下3×N的Jacobian阵;γ=［γ1，…，γN］T为 N 个 VSCMG 的框架角，［Ω］d=diag{Ω }，Ω =［Ω1，…，ΩN］，At=［t1，…，tN］为横向方向矩阵，As=［s1，…，sN］为转子转速方向矩阵.

2 操纵律设计

VSCMG操纵律设计的核心就是根据期望的力矩指令，产生CMG指令(框架转速指令)和RW指令(飞轮转速指令).如设CMG的期望力矩为TC，飞轮的期望力矩为TE，VSCMG总的期望力矩为Td，且TC+TE=Td，则可将式(4)分解为

如果针对式(5)、式(6)分别设计操纵律，同样可以得到实现期望力矩Td所需要的框架和飞轮转速指令.这样，即可将VSCMG操纵律的设计问题转化为CMG和RW的操纵律设计，只需分别计算C、E两个3×N矩阵的伪逆，而不用计算3×2N矩阵［C，E］的伪逆.然而，如果将操纵律分开设计，就必须考虑如何调度VSCMG的工作模式，将期望力矩Td分解为TC和TE.对于模式调度算法、CMG操纵律和RW操纵律的设计，将在以下部分逐一介绍.

2.1 模式调度算法

在VSCMG工作模式的调度中，总的原则是:当航天器处于姿态机动状态时，判断CMG是否远离奇异.如远离奇异，仅以CMG模式工作，产生大的输出力矩;一旦CMG接近奇异，引入RW模式与CMG模式配合，以VSCMG模式工作，协助VSCMG回避奇异.而当航天器处于姿态稳定状态时，可采用单纯的RW模式工作，输出精细控制力矩.

在模式调度的具体实施中，可首先判断航天器是处于姿态稳定状态，还是处于姿态机动状态.如果处于姿态稳定状态，直接令VSCMG进入纯RW模式工作.如果处于姿态机动状态，还需通过CMG奇异状况的判断来确定具体工作模式.对于航天器的控制状态，可通过姿态偏差及姿态角速度的大小来判断.如果姿态偏差及姿态角速度均较大，则认为航天器处于姿态机动状态.反之，则认为处于姿态稳定状态.具体判断方法比较简单，在此不赘述.在纯RW 模式下，TC=0，TE=Td.

对于CMG奇异状况的判断，通常定义奇异测度

来表征CMG构型距离奇异状态的远近.ε越大，表明框架构型离奇异状态越远;反之，离奇异状态越近.式(7)定义的奇异测度虽然可以准确反映矩阵At的奇异状况，但不能准确反映CMG构型是否奇异.实际上，只有当N个CMG产生的力矩都位于同一平面内而期望力矩垂直于这一平面时，才认为CMG发生了奇异.如果CMG奇异，矩阵At必定奇异;矩阵At奇异，CMG不一定奇异.因此，可从奇异的定义出发，定义参数分别表征CMG和RW的力矩产生能力.ε1越大，表示CMG力矩与期望力矩的夹角越小，CMG产生期望力矩的能力越强，离奇异越远.反之，则代表CMG产生期望力矩的能力越弱，越接近奇异.因此，ε1对CMG奇异的表征更为准确，可用来对CMG接近奇异的情况进行判断，从而确定工作模式.

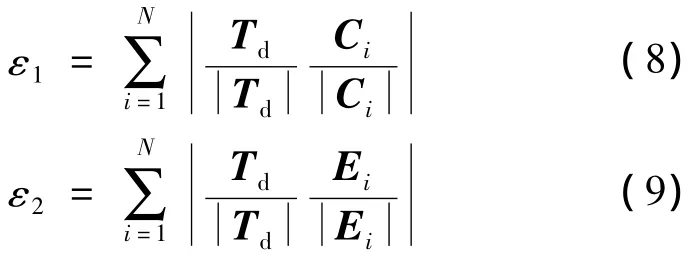
为此，可设定一个阈值α＞0.当ε1≥α时，CMG力矩与期望力矩的夹角较小，产生期望力矩的能力较强，可以令VSCMG工作在纯CMG模式，TC=Td，TE=0.

当ε1＜α时，CMG接近奇异，产生期望力矩的能力较弱，甚至会失去产生期望力矩的能力.由于CMG产生的力矩与RW产生的力矩相互垂直，因此，当ε1较小时，ε2必定较大.此时，可以让CMG直接逃离奇异，以RW产生力矩，令系统工作在VSCMG状态.如设CMG逃离奇异时产生的力矩为TCS，那么 TE=Td－TCS.

为使CMG可靠逃离奇异，可设定一个最优的目标框架角γd，使ε1最大.γd的求取可根据式(8)进行，在此不赘述.为使CMG的当前框架角γt在Δt时间后变为γd，期望的框架角速度为:

当期望力矩Td=0时，式(8)、(9)奇异，可直接令 TC=0，TE=0.

2.2 CMG 操纵律

CMG操纵律可仿照SGCMG的操纵律进行设计.对式(5)求Moore-Penrose逆，可得到力矩产生指令

为避免框架奇异，需加入框架再构型的空转零运动.在此，选用梯度型零运动为

其中，kg为一正常数.根据式(11)～(12)，可以得到CMG操纵律为

2.3 RW操纵律

与CMG类似，对式(6)求Moore-Penrose逆，可得RW模式下的力矩产生指令为

另外，为保证每个转子转速都接近平均转速，飞轮的转子转速需具有转速均衡能力.这样，不但可以使VSCMG具有良好的动量包络，还可以避免VSCMG系统因某个转子转速过高引起饱和或过低导致VSCMG失去大力矩输出能力.为此，需在飞轮模式的操纵律中加入一个使各转子转速向平衡转速靠近的空转零运动.仿照文献［7］，可设计转速均衡的零运动具体形式为

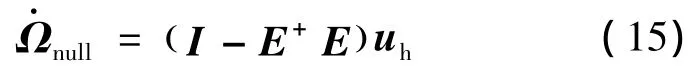
其中，uh为N维矢量的列向量.确定空转零运动的要点就在于选择矢量uh.为此，定义一个指标函数来表征转子转速的平衡能力.具体函数为

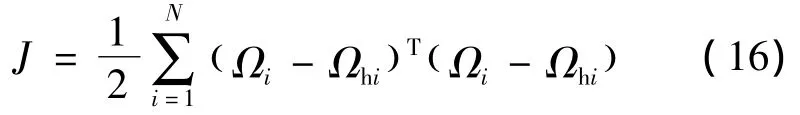
对式(16)两端求导，可得

根据式(17)，可以得到式(16)表示的空转零运动对指标函数J的影响为

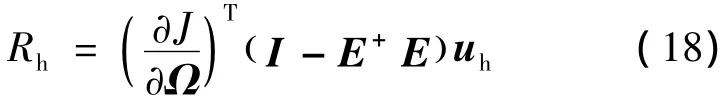
令

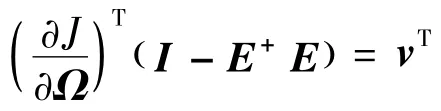
则式(18)可变为

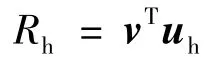
要保证转子转速均衡，J应尽量小，故应使Rh为负.因此，可取uh=－khv，kh为一正常数.将uh代入式(15)中，可得到使转子转速均衡的空转指令为

根据式(14)和式(19)，可以得到RW操纵律为

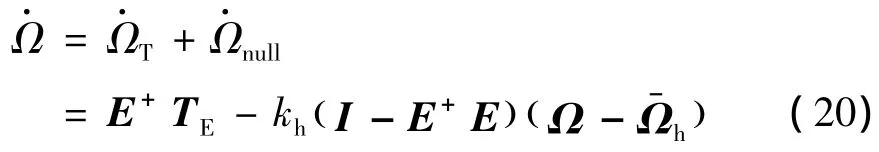
3 数值仿真

为验证本文操纵律的有效性，在此以金字塔构型的某4-VSCMG系统为例，针对几种典型输入进行仿真.仿照文献［11］，选择仿真参数如下:系统初始框架角为 Ω0=［0°0°0°0°］T，转子初始转速为 Ω0=［523523523523］T(rad/s)，Iws=diag{0.7，0.7，

为简化计算，在仿真中对系统的角动量进行了归一化处理.设Ωn=523rad/s为飞轮的标称转速，则每个VSCMG转子的标称角动量为IwsiΩn.将每个VSCMG的角动量矢量hisi除以IwsiΩn，即对系统的角动量进行了归一化处理.

针对以下两种情况进行仿真:一是不采用模式调度算法，以纯CMG模式工作，相当于SGCMG;二是采用模式调度算法，自动进行模式切换.对比两种情况下的仿真结果，可知在大多数情况下，系统由于没有出现不可回避的奇点，CMG和VSCMG的工作性能基本相同，具体仿真曲线略.

当期望力矩为Td=［100］T，CMG遇到不可回避的内部椭圆形奇点［14］γ =［－90°0°90°0°］T，两种情况下的仿真结果如图1～2所示.

图1 Td=［100］T时CMG操纵律仿真曲线

图1是以纯CMG模式工作的仿真结果，不进行模式切换.可以看出，当CMG的框架角γ=［－90°

0° 90° 0°］T时，奇异测度变为0，框架角速度陷入奇异状态无法逃离，出现“死锁”现象，CMG模式失效.

图2是采用模式调度算法自动进行模式切换下的仿真结果.可以看到，当CMG接近奇异时，RW开始工作，进入到VSCMG工作模式.同时，对CMG主动施加一逃逸框架角速度，使框架角逐渐逃离奇异状态.在CMG逃离奇异过程中，由于RW产生的力矩很小，所以会有较大的力矩误差.逃离奇异状态后，系统重新进入CMG模式，直至饱和.

综上所述，可知采用模式自主调度的VSCMG操纵律，可有效逃离SGCMG不可回避的奇点.

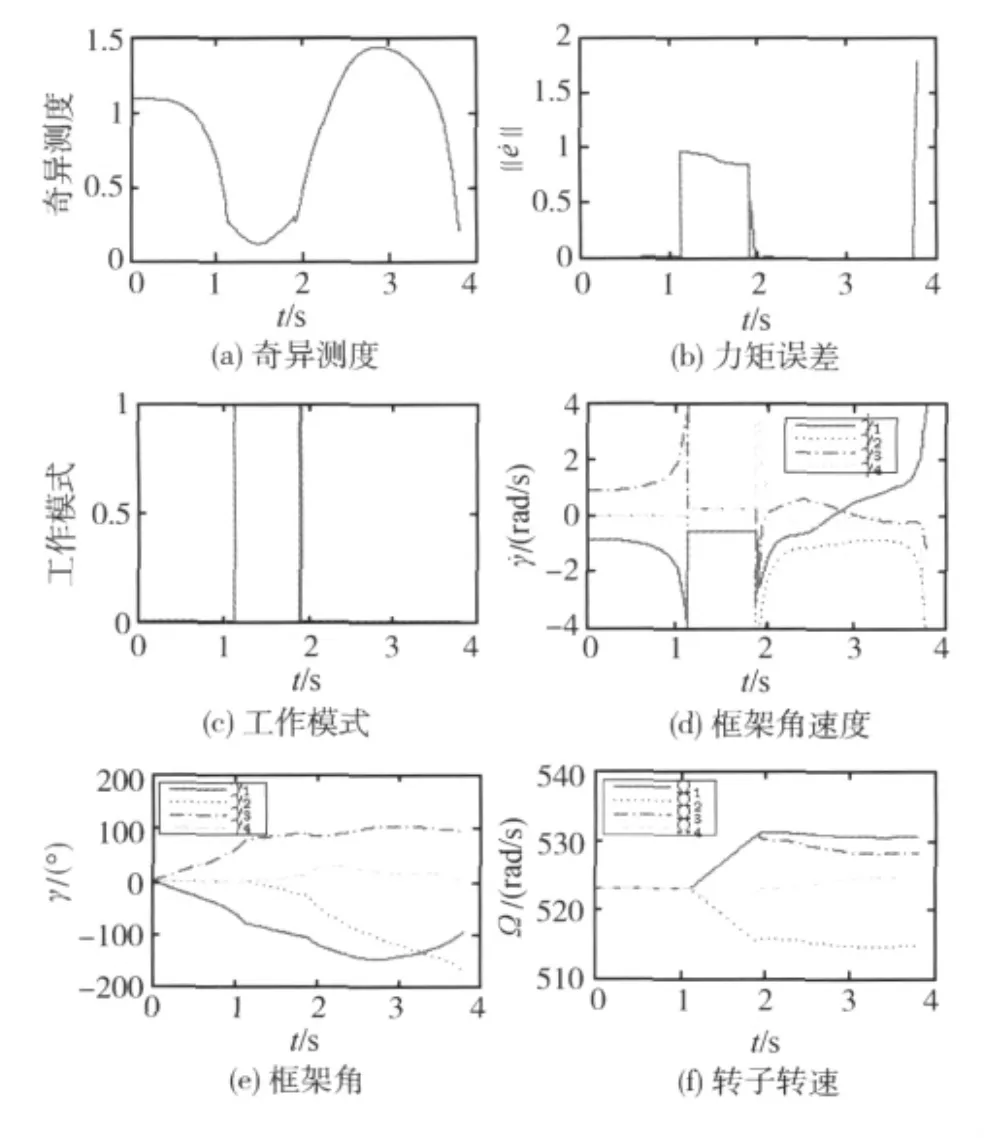
图2 Td=［100］T时模式调度操纵律仿真曲线

4 结论

本文充分考虑VSCMG的特点，设计了一个工作模式自主调度的操纵律.当系统远离奇异时，仅以CMG模式工作，产生大的输出力矩.当系统接近奇异时，引入RW模式与CMG模式配合，以VSCMG模式工作，协助VSCMG回避奇异.当处于姿态稳定模式，采用单纯的RW模式工作，提供精细的姿态控制力矩.同时，此操纵律把一个3×2N的矩阵求伪逆问题分解为两个3×N的矩阵求伪逆问题，计算简单，更易于实现.

［1］ Yoon H，Tsiotras P.Singularity analysis of variablespeed control moment gyros［J］.Journal of Guidance，Control，and Dynamics，2004，27(3):374-386

［2］ Alexandre N P.Feedback-based steering law for control moment gyros［J］.Journal of Guidance，Control，and Dynamics，2007，30(3):848-855

［3］ 刘军，韩潮.应用变速控制力矩陀螺的微小卫星大角度姿态机动控制［J］.空间科学学报，2007，27(4):336-341

［4］ 金磊，徐世杰.采用单框架控制力矩陀螺和动量轮的航天器姿态跟踪控制研究［J］.宇航学报，2008，29(3):916-921

［5］ 刘军，韩潮.使用变速控制力矩陀螺的航天器鲁棒自适应姿态跟踪控制［J］.航空学报，2008，29(1):159-164

［6］ 贾英宏，徐世杰.采用平行构型的变速控制力矩陀螺群的航天器姿态控制［J］.宇航学报，2003，24(5):490-495

［7］ 邢林峰，孙承启，汤亮.高姿态稳定度敏捷卫星的VSCMGS操纵律研究［J］.空间控制技术与应用，2008，34(6):24-28

［8］ 汤亮，徐世杰.采用变速控制力矩陀螺的航天器自适应姿态跟踪和稳定控制研究［J］.航空学报，2006，27(4):663-669

［9］ Oh H，Vadali S.Feedback control law for variable speed control moment gyros［J］.Journal of the Astronautical Sciences，1998，46(3):307-328

［10］ Schaub H，Junkins J L.Singularity avoidance using null motion and variable-speed control moment gyros［J］.Journal of the Guidance，Control，and Dynamics，2000，23(1):11-16

［11］ Yoon H，Tsiotras P.Spacecraft adaptive attitude and power tracking with variable speed control moment gyroscopes［J］.Journal of the Guidance，Control，and Dynamics，2002，25(6):1081-1090

［12］ 贾英宏，徐世杰.利用变速控制力矩陀螺的航天器集成能量与姿态控制［J］.航空学报，2007，28(3):647-653

［13］ 贾英宏，徐世杰.采用变速控制力矩陀螺的一种姿态/能量一体化控制研究［J］.宇航学报，2003，24(1):32-37

［14］ 张景瑞.基于奇异值分解的 SGCMG操纵律分析［J］.应用数学和力学，2008，29(8):948-925