贴片及引脚式LED芯片连接的热应力应变对比分析

隋 越(闽江学院物理学与电子信息工程系，福建 福州350108）

目前，发光二极管(Light Emitting Diode，LED）被认为是具有巨大发展潜力的新一代照明光源，而其实际发光效率较低，例如芯片发出的光能只占总输入能量的20%，另外接近80%的电能转化成为了热能[1]。对于高功率LED，良好的散热是维持其稳定工作的关键，许多关于LED热管理的研究都集中在散热封装上[2-3]，而引脚的应力常被研究者所忽视。芯片的失效中的很大一部分与芯片和引脚的接触状况有关，关于芯片-引脚应力应变分布研究较少。

LED芯片的典型封装方式有2种，其中1种是贴片式，在该封装形式下芯片及2个引出脚和封装底板紧贴在在一起；另1种是引脚式，即LED芯片和外界可通过引脚与电路板连接。在以上2种不同的封装方式中，芯片与外连接材料的模型及体积不一样。在建立上述2种连接的应力应变模型时，需要考虑芯片与外界环境之间的热传导，同时固体材料的应力应变又需要考虑结构力学中应力方程的应用，在方程耦合上需要深入研究。为此，笔者采用有限元方法，针对2种连接方式下LED芯片的发热和电路板之间的应力应变进行模拟，然后从应力应变角度分析2种典型封装失效的可能性大小。

1 应力应变模型和热传导模型

采用广义热传输和应力应变这2种稳态应用模型模拟LED芯片的连接方式。首先绘制出LED芯片的三维图形，如图1所示。

在图1（a）中，其上较长的矩形为发热芯片，厚度为0．5mm，长宽分别为6mm和1．5mm；芯片为GaN半导体材料，其下较大的矩形为电路板FR4材料，发热芯片与基板之间采用焊锡连接，焊锡的成分为锡和铅(两者比例为0．6∶0．4）。在图1（b）中，发热芯片的尺寸与基板之间采用金属引脚连接，材料为银。

应力σ与应变ε之间关系用下式表达[4]：

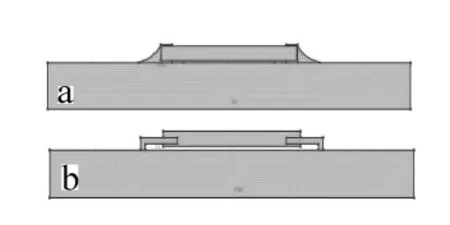
图1 贴片(a）及引脚式(b）连接的LED芯片

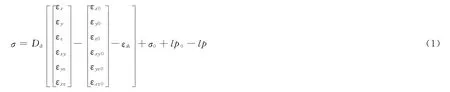
式中，σ为各方向的应力，GPa；εx、εy、εz、εxy、εyz、εxz分别为各方向上的应变；εx0、εy0、εz0、εxy0、εyz0、εxz0分别为各方向上的初始应变；εih为热应力引起的应变；σ0为初始应力，GPa；l为列向量，p和p0分别为材料内的压力和初始压力，GPa；Dd为材料的弹性矩阵。

对于各向同性的材料，其弹性矩阵形式为：

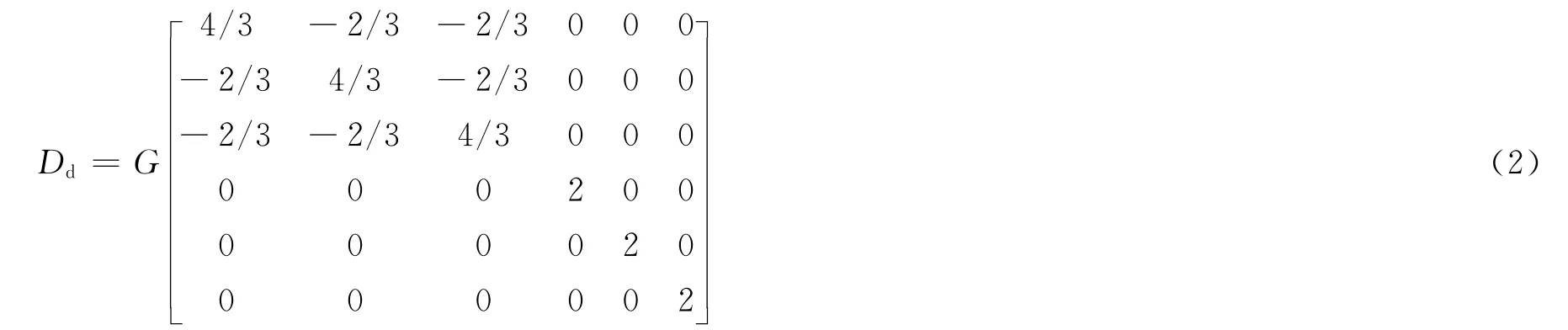
材料内的压力：

材料内的初始压力：

式中，G为剪切模量，GPa；N为材料体积模量，GPa；剪切模量和材料体积模量都可由杨氏模量E和泊松比ν求得[2]；σ0x、σ0y、σ0z分别为材料中各方向的初始应力，GPa。

在模拟过程中，采用广义热传导模型模拟材料中的传热，其方程如下[5]：

式中，k为热材料及连接材料的热导率，W／（m·K）；T为温度，K；qs是LED芯片单位体积的发热密度，取值为48mW／m3（LED芯片的总功率为0．2W）；ρ为材料密度，kg／m3；cp为各种材料的定压热容，J／（kg·K）；u为模拟模型中各种材料（包括空气和固体材料）的流速，m／s。

模型中所用材料性能参数如表1所示。

基于Matlab的Comsol软件建立程序。由于芯片为长方体形状，在模拟过程中只考虑芯片的一半，对芯片-引脚-电路板组合的网格剖分如图2所示。

为了更准确地研究引脚处温度和应力分布，将引脚处的网格剖分更细致。图2中边界a为对称边界，b为固定边界，c为开放边界。在模型中各个部分的连接边界的温度和热通量取为连续条件。

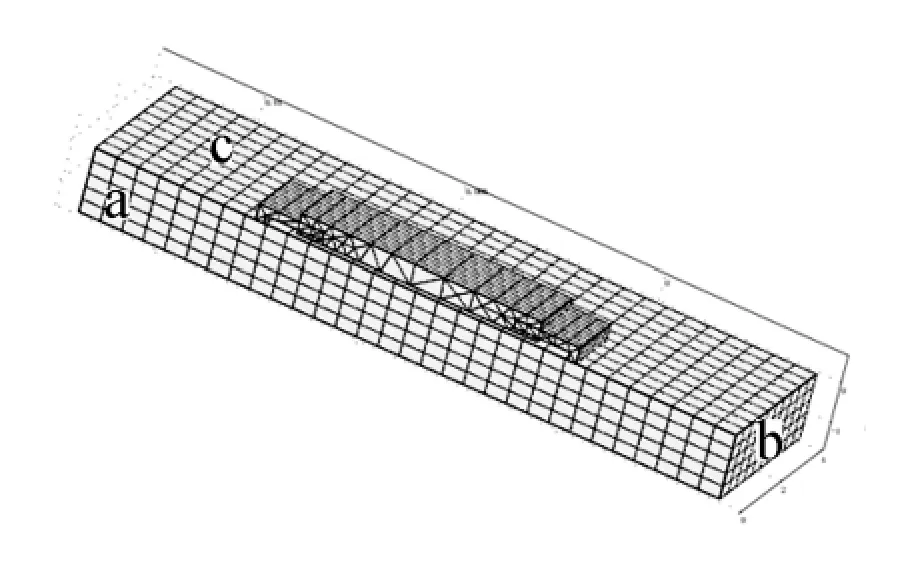
图2 芯片-引脚的有限元网格剖分

2 模拟得到的温度分布

对图2中的芯片及电路板上面的空气流进行剖分之后，将式(1）和式(5）化成差分形式，再对整个空间的温度和应力应变进行计算，获得LED芯片的2种连接方式的温度分布，最后得到三维温度场(见图3）。

由图3可以看出，2种芯片周围的温度分布差别很大，其温度分布具有如下特征：①贴片式芯片与下面接触热沉之间的温度连续变化，温度梯度相对较小，而引脚连接芯片周围的温度梯度较大；②贴片式LED芯片下面的PR4材料温度与芯片温度变化不大；③计算得到贴片式连接芯片表面最高温度为423K，而引脚式连接的温度最高温度为526K。上述特征说明在相同输入功率(0．2W）条件下，贴片连接方式有助于芯片散热。

3 2种连接方式下的应力应变分布

在给出温度变化的同时，得到2种连接方式下材料中的应力应变分布，如图4所示(材料表面的箭头表示应变释放方向）。

图3 贴片(a）及引脚式(b）连接的LED芯片周围温度分布

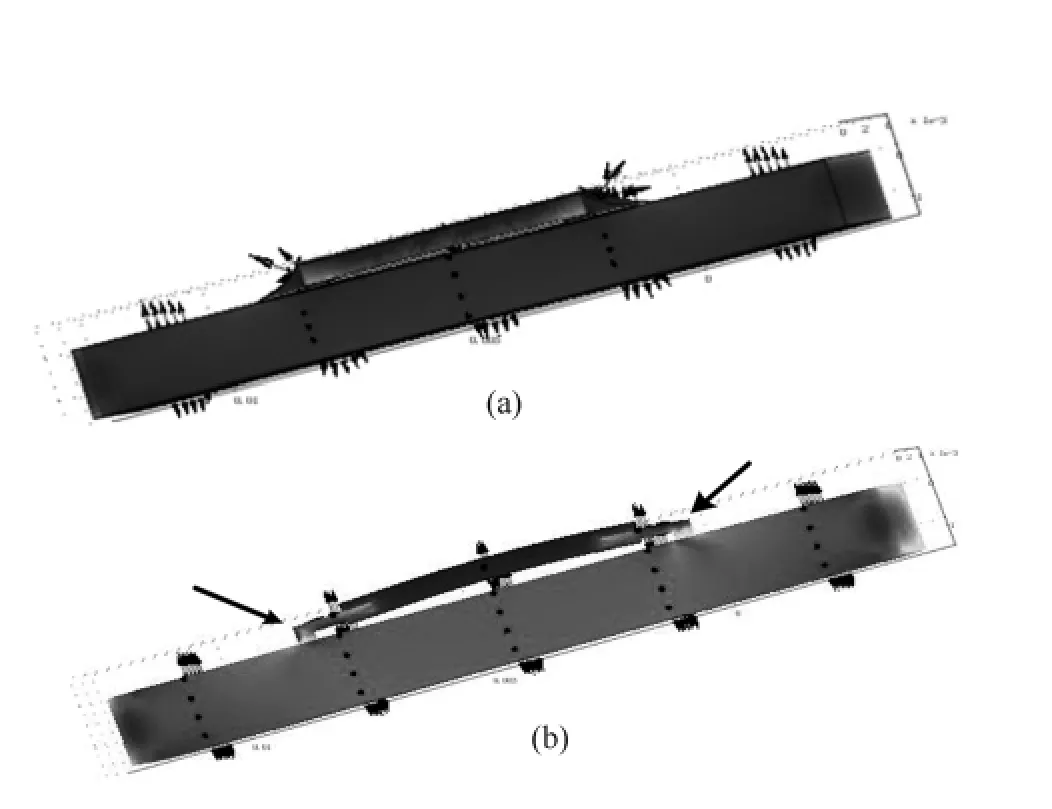
图4 贴片(a）及引脚式(b）连接的LED芯片 应力应变侧视图

从图4可以看出，2种连接情况下应变都是沿着垂直于表面的方向释放的。这是由于贴片连接情况下焊锡表面为曲面，其表面的释放空间更大。此外，贴片式芯片的应变明显小于引脚式连接芯片的应变，其原因是由于引脚式连接情况下在银引脚与FR4的接触点温度梯度较大，因而该点的应变数量也会超过贴片式连接的应变。

为了更清楚地观察材料的应变，给出2种装配方式下材料内部位移曲线，如图5所示。从图5可以看出，在2种装配形式下，边沿的应变分布比较相似，但在发热芯片引出点有较大的差别；在引脚式的银引脚中的位移曲线数密度少于贴片式的焊锡中的位移数密度。

由于位移曲线占据空间只能表明应变释放空间的体积，不能说明应变总量的大小，因而对芯片材料的总位移进行积分计算，其结果如表2所示。表2中的位移积分数值来自图5中内侧面，侧面的形状大小为图1所示。该侧面的边界条件为连续边界条件，位于LED芯片封装的正中间。表2中的Z方向为图1所示垂直方向。

图5 2种连接的芯片内部位移曲线

由表2可以看出，相同芯片在2种不同的装配方式下，引脚式封装引起的位移大约是贴片封装的位移的3倍。此外，2种封装形式下位移主要沿着Z方向（其原因是模型中的XY方向处于材料内部，而应力只能在芯片与引出点的外表面释放）。根据上述分析，可以得到如下结论，即贴片式连接释放的空间更大，同时其应变产生的位移数值小于引脚式连接的位移数值，由此说明贴片式连接可靠性更高。

表2 2种连接方式下的表面位移

4 结 语

采用有限元方法对2种LED芯片连接方式进行模拟，获得2种LED封装下的温度分布及应变分布。研究表明，在不同的装配方式下，芯片的电路引出部分的热导系数对芯片散热并不起主导作用，芯片散热主要由与其表面接触的材料和连接处的应变释放空间决定，贴片式连接的应变数值小于引脚式连接应变数值，同时贴片式连接产生的应变释放空间更大，说明在相同的装配工艺下贴片式封装比引脚式封装的可靠性要高

[1]Lin Y C，Nguyen T，Zhou Y，et al．Materials challenges and solutions for the packaging of high power LEDs [A]．Int Microsystems Packing Assembly Conference [C]．Taiwan，2006：177-180．

[2]Barton D，Osinski M，Perlin P，et al．Life Test and Failure Mechanisms of GaN／AlGaN／InGaN Light Emitting Diodes [A]．Prcoce．SPIE [C]．San Jose CA，1998，3279：17-27．

[3]苏达，王德苗 ．大功率LED散热封装技术研究的新进展 [J]．电力电子技术，2007，41（10）：13-15．

[4]Lu H，Bailey C，Dusek M，et al．Modeling the Fatigue Life of Solder Joints of Surface Mount Resistors [A]．EMAP 2000 [C]．Hong Kong，2000：136-142．

[5]Angel V V，Petko H M，Tamara G P，et al．Thermal processes modeling during soldering of BGA components to PCB [J]．Electronics，2008，24：127-132．