优化批处理机排序方案的启发式算法研究

林烈青，郑 睿

LIN Lie-qing1,ZHENG Rui2

（1. 广东工业大学，广州 511495；2. 上海市浦东新区改革与发展研究院，上海 200127）

0 引言

根据工件加工类型的不同情况，目前文献所研究的批处理机排序方案可分为以下四类：

第一类是只包含一种工件加工类型的批处理机排序方案[1,2]。第二类称为compatible job families，是指工件包含多种加工类型，但是不同加工类型的工件可以放在同一个批次中一起加工，且每一类加工类型的工件所需加工时间相同[1,3]。第三类称为incompatible job families，是指工件包含多种加工类型，只有同种加工类型的工件才能放在同一个批次加工，而且同种加工类型的工件所需的加工时间是相同的[4,5]。第四类称为family jobs，是指工件包含多种加工类型，只有同种加工类型的工件才能放在同一个批次加工，但是同种加工类型的工件所需的加工时间是不相同的。因此每个批次的实际加工时间取决于该批次工件所需加工时间的最大者。

本文研究的属于分批调度问题中的第四类family jobs，而且工件之间带有链式先后关系约束，文献[6]对该类问题进行了初步研究。总的来说，国内外对于这类批处理机排序方案的研究还不够深入，用于求解排序方案的算法较为少见。为此，本文设计并验证两种批处理机排序方案的启发式算法，以找出综合效果更好的算法。

1 问题描述

本文中，排序方案的目标函数为最小化加权完工时间和，而且批量无限制，描述如下：

有n个工件要在同一台机器中进行加工。这些工件属于m种不同的加工类型。每个工件记为Jij，其中下标i表示该工件属于第i种类型，下标j表示该工件在第i种类型工件中的编号。第i种类型工件的数量记为ni，因此有ni＝n。每个工件所需要的加工时间记为pij，权重记为wij，i＝1，2，…，m，j＝1，2，…，ni。只有属于同一种类型的工件才能被放入同一批次中，在机器中同时被加工。工件可以分成r个批次，分别记为B1，B2，…，Br。

每批的加工时间和权重分别记为P(Bl)和W(Bl)，l＝1，2，…，r。由于同一批的工件同时被加工,并且同时被释放，所以同一批的工件具有相同的完成时间，同一批的工件的实际加工时间等于该批工件中所需加工时间最大者，即第l批的加工时间P(Bl)＝maxJij∊Bl{pij}。而每批的权重等于该批所有工件的权重和，即

另外，工件之间存在着链式先后关系约束，存在若干组工件满足以下形式的约束关系：

其中符号A→B表示工件B的加工只有在工件A完工以后才可以开始，因此，这里A称为B的前驱工件，B称为A的后续工件。并且设定这些约束关系链的最大长度为k。

记工件Jij的完工时间为Cij，如果工件Jij属于生产中的第k个批次，该批次记为Bk，则工件的完工时间等于第k个批次的完成时间，即Cij＝本文中，问题的目标函数为最小化加权完工时间和，就是在符合加工类型约和工件先后关系约束的情况下，把工件分批并确定批的加工顺序,从而使得目标函数加权完工时间和的值最小。用三参数方法表示即为

2 排序方案的最优解性质

在求解排序方案最优解的算法之前，首先分析最优解的性质，可作如下定义：

定义1：在某个时刻t，如果一个工件Jij未被排序，而且该工件没有前驱工件，或者在该时刻这个工件的所有前驱工件都已经完工。那么称该工件Jij为在时刻t可以被排序的工件，符合这种条件的工件组成的集合记为JP (t)，因此Jij∊JP (t)。

对于上面排序方案的最优解，有引理如下：

引理1：在本方案的最优解中，如果某个批次Bt的加工开始时间是时刻t，而批次Bt中含有工件Jij。那么在此最优解中，时刻t可以被排序的工件集合JP (t)中所包含的工件Jij同类型，且所需加工时间不大于工件pij的工件，都应该在批次Bt中，即

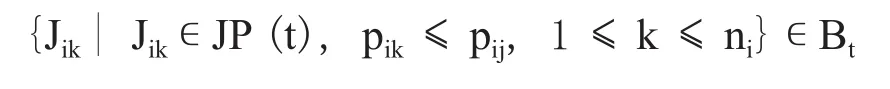
该引理可用反证法证明成立，限于篇幅不再详述。

3 启发式算法的设计与实现

文献[6] 证明了此类排序方案是强NP-hard问题，所以不可能找到多项式时间的最优算法，在可接受的时间范围内找到一个和最优解结果相差不大的排序方案即可，也就是在合理的时间内找到一个满意解。

文献[6]给出了一种求解该问题的启发式算法，即满批算法（Full Batch，FB）。为了有更多的算法可供选择，并寻求更高效率的算法，在这里提出两种新的启发式算法。

第一种启发式算法称为贪婪算法。其工作原理是把加工时间相近的工件放在同一批中，可以节省加工时间，提高工件加工的效率。根据引理1，如果在一个批次中加入了一个未排序的工件Jij，那么在该批次加工开始时间t可以被排序的所有所需加工时间不大于pij的属于加工类型i的工件都应该加入到这个批次中。所以在该算法中，在时刻t只允许生成包含在可排序工件集合JP (t)内，同一类型工件SPT排列中具有从1开始的连续编号工件的批次。这里，把时刻t可能组成的可行的批次记为Bl(t)＝B (Ji1(t)，Jiv(t)) (l＝1，… ，K)，表示批次属于i型批次，Ji1(t)表示批次的起始工件，即JP (t)内i类型工件SPT排列中的第一个工件；Jiv(t)表示批次的末尾工件，即JP (t)内i类型工件SPT排列中的第v个工件。也就是说一个可行的批次可以由末尾工件来确定。即B (Ji1(t)，Jiv(t))＝{Ji1(t)，Ji2(t)，… ，Ji,v-1(t)，Ji,v(t)}，其中i＝1,… ，m，v＝1,… ，ni。所以在本算法中每次总共最多会生成k≤n个不同的可行批次。贪婪算法流程如下：

3.1 贪婪算法（Greedy Ratio,GR）

步骤1：算法开始，当前时刻记为t，当前已排序方案记为S (t)，当前已排序方案的最后一个批次的完工时间为t，此时t＝0，S (t)＝0/。

步骤2：记在当前时刻t可以被排序的工件集合为JP (t)，如果该集合为空集，则直接跳到步骤4。否则，按照上述的规则生成当前时刻t的所有的可行批次，即只包含具有在JP (t)内同一类型工件SPT排列中从1开始的连续编号工件的批次，记为Bl(t)，l＝1，…，K。因此我们可以得到一个可行批次的集合Β＝{Bl(t) | l＝1，…，K}。

步骤3：从集合B中选择一个具有最小的批次加工时间/权重比率，即P (Bl(t)) / W (Bl(t))的批次Bl(t)∊B，把它安排进入排序方案中，紧挨着已经排定的批次之后进行加工（如果前面没有已排定的批次，则安排作为第一个批次），所包含的工件均已排序。另外，更新当前时刻为t+P (Bl(t))，更新已排序方案为S (P (Bl(t)))＝S (t)∪Bl(t)，然后回到步骤 2。

步骤4：所有工件已排序，得到最终完整的排序方案，算法结束。

第二种启发式算法称为优选算法（BEST）。这是一种混合算法（composite heuristic），整合了前面的两种启发式算法（文献[6]中的满批算法和上述的贪婪算法）。该算法的动机在于，不同的启发式算法在不同的环境中的表现各有优劣，如果只单独使用一种算法，可能会在某些情况下效果很差。但是如果联合使用几种算法，就能取长补短，达到优选的效果。而且启发式算法本身耗时很少，因此同时使用多种算法的总耗时也不会很多，所以利大于弊。因此本算法的基本思想就是每次对同样的问题同时使用前面的两种算法，并从中选取最好的排序方案，作为算法的排序方案。优选算法流程如下：

3.2 优选算法（BEST）

步骤1：应用以上的两种算法（满批算法和贪婪算法）进行求解，得出两种排序方案。

步骤2：从上一步得出的两种方案中，选出目标函数值最优的一种组合，作为本算法的结果。

4 计算机仿真分析

4.1 实验设计

为了检验以上算法的结果和效率，采用计算机仿真实验的方法来对这些算法进行验证。在本实验中，所有算法均使用Visual Basic 6.0 编译实现，计算机模拟实验是在CPU为AMD Athlon XP 2000+，内存为1GB，操作系统为Windows XP 环境下进行。

实验的流程分为三步，第一步是要随机生成一些算例；第二步是用上述的算法来求解这些算例；第三步就是要把这些算法求解的结果进行汇总和分析。算例涉及到的参数有以下几个：工件个数n，工件类型数m，平行链长度k，工件所需加工时间pij和权重wij。在本实验中，工件数量n的取值是n＝20，工件类型数m的取值是m＝4。在实验中，采取服从一定分布下的数据随机生成的办法来生成每个算例的参数。其中，每个工件的加工类型i将服从区间为U [1,4]的均匀分布；而对于工件的加工时间pij和权重wij，为了能够出现更多的不同的情况，在随机生成工件数据的时候，采用方差较大的均匀分布。加工时间pij采用两种情况的均匀分布U [1,10]和U [1,20]，分别代表了范围较小和范围较大的情况；工件权重wij采用了两种情况的均匀分布U [1,10]和U [1,20]，也分别代表了范围较小和范围较大的情况（注：其中U [a,b]表示上限为b，下限为a的均匀分布）。因此，一共会有2×2＝4种不同的加工时间和权重的组合。每种组合随机生成20个算例进行计算，总共要计算4×20＝80个算例。

加工先后约束关系应该是多条长度相等的平行链，取平行链的长度为4，即k＝4。所以对于20个工件的问题，应该有5条平行链。在这5条平行链，就会有20个对应的位置，记为PO (i)，i＝1，…，20。也就是说，这20个位置满足这样的先后关系约束：PO (l－1)×4＋1)→PO (l－1)×4＋2)→PO (l－1)×4＋3)→PO (l－1)×4＋4)，l＝1，…，5 。每个工件随机生成一个0到1之间的数，称为该工件对应的随机键，按每个工件对应的这个随机键的升序对这些工件进行排列，在这个排列中位于第1位的工件，则进入位置PO (1)，在这个排列中位于第2位的工件，则进入位置PO (2)，以此类推，这样所有20个工件就会在平行链中有对应的位置。这样，就生成了每个算例中的工件的加工先后关系约束。

对于每一个算例都会用本文提出启发式算法和文献[6]中的满批算法来求解，并用分支定界算法求得每个算例的最优解。本实验用分支定界算法求得的最优解作为标杆，检验启发式算法求得的结果和最优解之间的比率。对每个随机生成的算例，先用分支定界算法求得最优解，并计算该最优解的目标函数值。然后用上述的启发式算法求得近似解，并计算这些近似解的目标函数值，最后用后者除以前者，得到一个比率。显然这个比率是一个不小于1的数，而这个比率越接近1，就表示启发式算法求得的解越接近最优解。

4.2 实验结果分析

下列图1～图4分别表示了工件加工时间和权重的取值区间为[1,10]和[1,10]， [1,10]和[1,20]，[1,20]和[1,10]，[1,20]和[1,20]时算法结果和最优解比率的波动情况。其中横坐标表示每种参数组合中实验的序数，即表示这是第几次的实验结果，而纵坐标表示的是各算法结果与最优解的比率值。

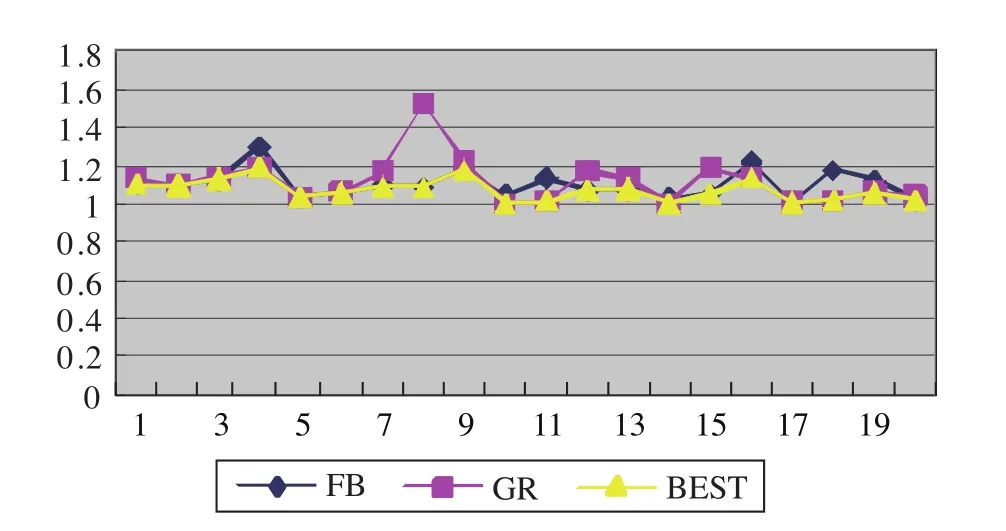
图1 启发式算法结果与最优值的比率（p：[1,10],w：[1,10]）

图2 启发式算法结果与最优值的比率（p：[1,20],w：[1,10]）

图3 启发式算法结果与最优值的比率（p：[1,20],w：[1,20]）

图4 启发式算法结果与最优值的比率（p：[1,10],w：[1,20]）

实验结果如表1和表2所示，表中的数据主要是启发式算法求出目标函数值与分支定界算法求出的最优目标函数值之间的比率。例如FB表示满批算法（FB）求出的解的目标函数值与分支定界算法求出的最优目标函数值之间的比率。

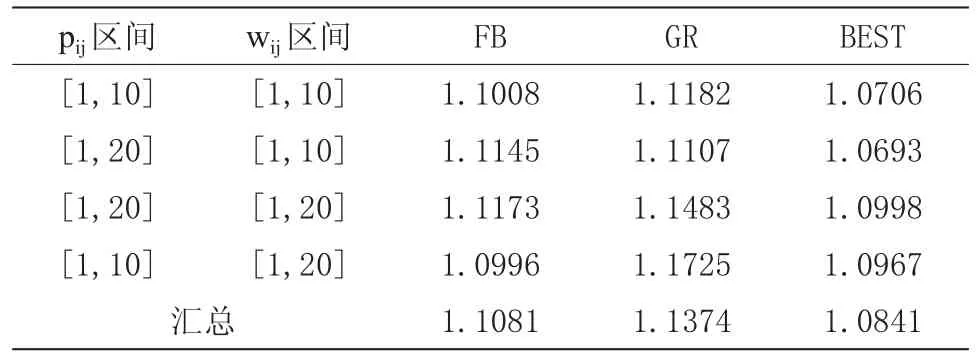
表1 启发式算法结果与最优值的比率汇总（平均情况）

表1表示的是平均情况，即比率的平均值；而表2表示的则是比率值最差的情况，即比率的最大值。下面将分别从算法结果和算法耗时两个角度来分析本实验的结果。

表2 启发式算法结果与最优值的比率汇总（最差情况）

从算法所得解的目标函数值的比率来看，表1和表2的数据表明无论是平均情况还是最差情况，结果最好的都是优选法（BEST），而且无论工件参数如何变化，优选法的结果都非常稳定。从耗时的角度来看，满批算法和贪婪算法的耗时都非常小，均不超过0.1秒，优选法的耗时为两者之和，也几乎可以忽略不计。因此，优选法的综合效率最高。

5 结论

工件带有链式先后关系约束的family jobs类型的批处理机作业排序调度问题是一个非常复杂的问题，它属于强NP-hard问题。本文分析了作业排序方案的目标函数为最小化加权完工时间和，并且得出了最优解的性质。根据最优解的性质设计了求解排序方案的两种启发式算法---贪婪算法和优选算法，通过计算机仿真实验结果表明，优选算法比现有文献的启发式算法综合效率更好，可作为实际应用中的首选。

[1] Brucker P,Gladky A,Hoogeveen H,et al. Scheduling a batching machine[J]. Journal of Scheduling,1998,1：31-54.

[2] 冯大光,唐立新. 单台批处理机总加权完成时间最小化的启发式算法[J].控制与决策,2006,21 (11)： 1293-1297.

[3] Chandru V,Lee C and Uzsoy R. Minimizing total completion time on a batch processing machine with job families [J]. Operations Research Letters,1993,13： 61-65.

[4] Uzsoy R. Scheduling batch processing machines with incompatible job families [J]. International Journal of Production Research,1995,33： 2685-2708.

[5] Jolai F. Minimizing number of tardy jobs on a batch processing machine with incompatible job families [J]. European Journal of Operational Research,2005,162：184-190.

[6] Zheng R,Li H.Y. Minimizing total weighted completion time on a batch-processing machine with re-entrance[C].Proceedings of the IEEE International Conference on Automation and Logistics,Shenyang,China,August 2009：1791-1794.