复杂地形条件下高填方及其支挡结构的整体稳定性分析

邢月龙，朱天浩，沈恺伦，欧晓晖

（1.浙江省电力设计院，杭州市，310012；2.中国电力企业联合会，北京市，100070；3.浙江大学岩土工程研究所，杭州市，310027）

0 引言

舟山与大陆联网输电线路工程大猫山主跨越塔为目前最高的跨越铁塔，塔基位于地形急剧变化的山体陡坎处，基础周边地质条件异常复杂。3、4号基础外侧存在深厚的淤泥层，而且由于地势较低，需填方近20 m。经过分析，结合本工程的实际情况，初步确定的原则方案主要有：（1）采用放坡方案，对软土地基进行处理；（2）避开软土地基，在施工平台外淤泥层较浅处设置挡土墙。

对方案（1），放坡回填前需对淤泥进行地基处理。考虑到淤泥层太厚（最厚处达到13 m），清淤换填的方案显然不合适。其他可能的软基处理方案有：排水固结法、振冲砂石桩、水泥搅拌桩和爆破挤淤法。前3种方案软基处理后，虽然竖向承载力可以满足要求，但是滑移稳定性仍然没有得到显著改善；如采用这3种方案，则还需在坡脚处设置沉井基础才能保证滑移稳定性，工期较长、费用也较高。对于爆破挤淤法，经过现场测量放样，塔位附近的养殖塘、大坝和水库均在爆破挤淤的直接影响范围之内，爆破挤淤技术对本塔位而言也不合适。

对方案（2），适合本塔位的挡土墙方案主要有：衡重式挡墙方案和加筋土挡墙方案。考虑到本塔位存在海水冲刷的影响，加筋土挡墙不宜低于海水冲刷的高度。因此，这2种方案转变为衡重式挡墙以及衡重式挡墙和加筋土挡墙组合方案（下部衡重式挡墙，上部加筋土挡墙）。这2种方案对本塔而言均是合适的，造价也相当，但是加筋土挡墙对施工工艺要求较高，同时所需工期也较长[1]。

综合考虑上述因素，大猫山370 m跨越塔3、4号基础外侧高填方区域采用了片石混凝土支挡结构。对如此高的支挡结构有必要从总体上对采用该方案后跨越塔塔基稳定性进行深入研究，对工程的安全性作出合理评价。

1 工程概况

舟山群岛地处我国东南沿海，长江口南侧，杭州湾外缘的东海洋面上。舟山与大陆联网输电线路工程为220 kV输电线路工程，其中螺头水道跨越部分按500 kV设计，是整个工程的核心。螺头水道主跨越段跨越档距为2 756 m，岛上2基高塔基础分别座落在舟山大猫岛和宁波凉帽山上。

本工程超高跨越塔塔基及基础存在以下特点：（1）基础体型巨大，最大单个基础平面尺寸为18 m× 18 m；（2）上部结构下传荷载量大且形式复杂，下压工况下单腿的压力达到10 000 kN以上，水平力也在1 000 kN以上；（3）塔基所处位置的地形和地质条件复杂，大猫山跨越塔位于地形狭窄的丘陵位置，塔基局部位于陡坎处，基底高差大，同时从地质条件看，基岩面高差大，岩性也较复杂，覆土厚度不均。

2 塔基支挡结构设计

大猫山岛的主跨越塔全高370 m，铁塔半根开为30.81 m，施工场地要求110 m×110 m。塔基地面标高为4.5～42 m（1985国家高程基准），设计高程20.0 m。

为达到设计高程以及跨越塔施工机械行走要求，须对原始山地进行开挖和回填平整。由于原地形呈西低东高走势，因此3、4号基础周围及其西侧施工场地为回填区。

回填区浅部地基土层主要为：①层素填土；②层淤泥；③层含角砾粉质粘土；④层强风化凝灰岩；⑤层中等风化凝灰岩。为填方区设计和分析计算需要，对填方区进行了勘察，典型地质剖面土体分层情况如图1。

图1 填方区典型地质剖面Fig.1 Typical geological profile of the embankment area

回填区主要采用开挖岩土体填筑，由于山脚养殖塘淤泥层较厚，且填方高度超过20 m，在征地范围内高填方稳定性难以保证。设计采用浆砌片石混凝土挡墙支护，挡墙基座入岩，墙趾反压回填，如图2。

图2 填方区剖面布置Fig.2 Retaining structure profile of embankment

3 整体稳定性研究

3.1 有限元模型的建立

由于输电塔3、4号基础回填区域地形和地质条件复杂，相应挡土结构及其与土体的相互作用较为特殊，常规计算方法不能满足计算分析和设计要求，须采用有限元方法进行计算分析。所用计算软件为荷兰Delft大学研发的专业岩土工程计算分析商业软件Plaxis[2]。软件可模拟岩土的分层特性，考虑了工程中岩土体与结构物之间存在的分界面的影响和静水压力、超孔隙压力影响；同时可以分阶段进行计算，模拟实际的施工过程，计算均假设岩土体变形为小变形。

在本构模型方面，针对不同材料采用了不同的弹性和弹塑性模型[3]。土工试验表明，弹塑性模型中莫尔-库仑强度理论比较符合岩土材料，同时莫尔-库仑强度理论的本构模型概念清晰，采用的参数少且易确定。该强度理论在岩土工程理论与实践中广为采用[4]，是一个对土工计算分析而言较理想的本构模型。其他材料如硬质岩体和混凝土等结构则采用弹性模型。

有限元方法能较好模拟施工全过程，并可利用土体强度折减法来模拟荷载作用下土体和支护结构的破坏过程，给出安全性评价。有限元法在稳定性研究方面概念清晰，易于编程实现，且可以清楚观察到破坏面位置与破坏的发展历程。有限元方法用于稳定分析已成为当前稳定性理论研究的发展方向[5]，Plaxis在整体稳定性分析方面采用的方法即为强度折减法[6-9]。

计算选择了3、4号塔基中部坡脚软土层最厚的剖面作为典型计算分析断面，如图2。对施工到正常使用期间全过程的有限元模拟主要集中在3个阶段：

（1）塔基施工结束后，挡土墙结构和墙后土体填筑施工完成，墙后填土经过压实后抗剪强度和变形模量有所提高，形成竖向和侧向荷载，同时挡土墙及其基础形成侧向挡土体系，该阶段处于施工期间，有部分沉降和侧向变形发生。

（2）墙顶形成施工平台，大型施工机械进场施工，机械行走和吊装等过程产生附加荷载，沉降和侧向变形进一步发生。其有限元计算模型及其网格划分如图3所示。

图3 Plaxis有限元计算模型及其网格划分Fig.3 Plaxis finite element method computation model and mesh generation

（3）场地的整体稳定性计算，这一阶段采用是强度折减法，该方法是在计算过程中通过将各层土体的抗剪强度指标按比例逐步减小，直到整个体系失稳破坏，通过起始点和破坏点的抗剪强度比较最终获得场地的整体稳定性安全系数。

3.2 支挡体系应力应变分析

在填方区场地堆填和挡墙砌筑之前，岩土体本身的应力场即初始应力场是有限元计算分析的基础。Plaxis有限元软件根据不同岩土体的容重计算各深度处的竖向有效应力，然后根据各层岩土体的力学性质（弹塑性体的抗剪强度指标或弹性体的泊松比）计算静止岩土体压力系数，从而得出水平向应力，最终得到一个适应于场地地形和地质情况的初始应力场。

支挡结构施工完毕后，在数值模拟的施工荷载和支挡结构自重的共同作用下，整个支挡体系发生相应位移，整体位移趋势为：挡墙底部入岩，几乎不发生位移；墙体整体略微向外倾斜，墙顶位移最大，同时墙后回填土体下沉；墙趾回填镇压区下卧深厚软土层，沉降较大，同时堆填体外侧有明显土体隆起发生。

墙背填土表面沉降分布和墙趾回填镇压区原地表沉降和外侧隆起分布如图4。从变形量看，由于挡墙墙基入岩，大大限制了墙体本身和墙后填土的变形，墙背填土沉降量远小于回填镇压区原地表沉降，前者不足后者的1/6。墙后填土地表沉降大致呈折线型分布，最大沉降发生在靠近挡墙约10 m的范围之内，最大沉降量约28 mm。墙趾回填镇压区沉降呈中间大两头小的分布方式，中间最大沉降177 mm，外侧隆起最大为76 mm。从位移分布看，设计使墙基入岩能有效抑制墙体和墙后填土发生较大变形，从而保证了跨越塔施工的顺利进行和塔基的稳定。

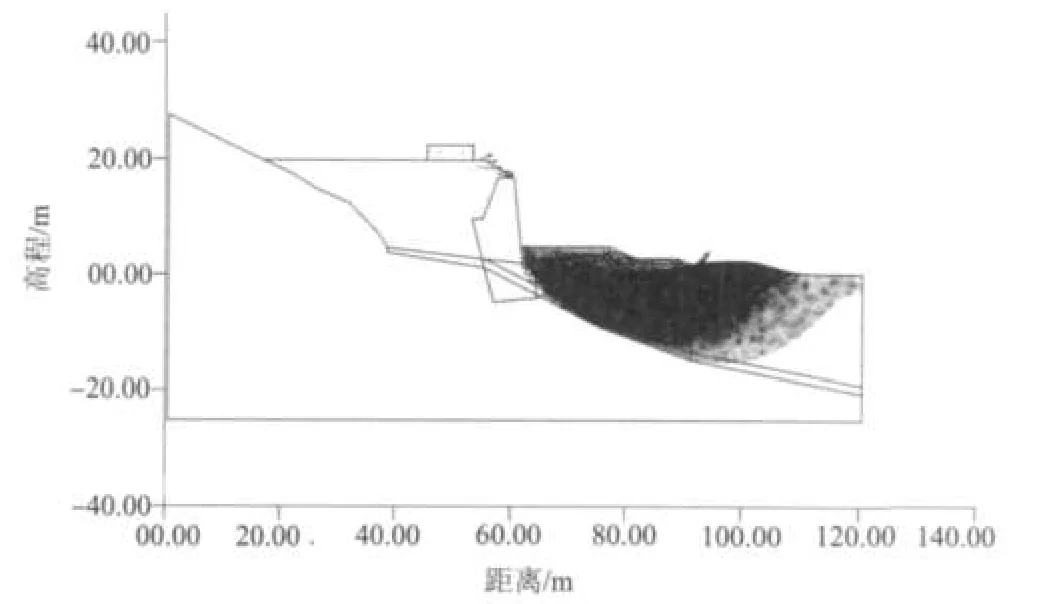
图4 整体稳定计算失稳破坏位移场Fig.4 Displacement field at failure with integral stability analysis

在数值模拟的施工荷载和支挡结构自重的共同作用下，整个支挡体系和周边岩土体应力分布发生明显改变。片石混凝土挡墙和墙下坚固岩体共同承担了大部分墙后填土自重和施工机械作业形成的荷载，表现为墙体下部和墙基附近岩体应力水平较高，墙趾附近有压应力集中现象，而墙前回填镇压区由于挡墙的支挡，软土区域应力分布较为均匀，有利于软土分布区域的稳定。片石混凝土挡墙墙趾有压应力集中现象，但应力水平不高，最大压应力不超过1.3 MPa，施工时应注意保证墙基有一定入岩深度，并保持该部位附近岩体完整。

3.3 整体稳定性分析

整体稳定性计算过程中人为使岩土体的抗剪强度降低到极限值时，场地发生整体破坏，破坏时场地位移矢量分布如图4。由位移分布形式可见，由于挡墙墙基入岩，挡墙本身片石混凝土结构也较为坚固，加之墙趾前方回填镇压层的设置，支挡体系本身整体稳定性较好。因此，整体稳定破坏发生在墙趾前方的回填镇压区，滑动面呈圆弧状，由强度折减法得到的计算剖面整体稳定安全系数为2.34。

4 结论

（1）片石混凝土挡墙为主体的填方区支挡体系能有效起到支挡填土体、限制位移和保持塔基整体稳定性的作用，由强度折减法得到的计算剖面整体稳定安全系数为2.34。

（2）挡墙墙基入岩使片石混凝土结构与其下岩体形成较好的支挡系统，承载了大部分墙后填土自重和施工操作产生的荷载，保证了挡墙内外的岩土体稳定。

（3）就挡墙本身而言，存在压应力和拉应力集中的现象，设计应考虑墙基趾部有一定入岩深度，并在拉应力区采取相应构造措施，同时施工过程中也应注意保持墙基岩体的完整性。

[1]朱天浩，徐建国，叶尹，等.输电线路特大跨越设计中的关键技术[J].电力建设，2010，31（4）：29-30.

[2]Brinkgreve R B J，Vermeer P A.PLAXIS version 8.2 Manual[M]. Rotterdam，Netherlands：A.A.Balkema，2002.

[3]沈珠江.土体结构性的数学模型：21世纪土力学的核心问题[J].岩土工程学报，1996，18（1）：95-97.

[4]李广信.高等土力学[M].北京：清华大学出版社，2004.

[5]黄永强，韩红桂.基于Plaxis的土石混填高路堤稳定性分析研究[J].公路工程，2008，33（6）：107-110.

[6]唐晓松，郑颖人，邬爱清，等.应用PLAXIS有限元程序进行渗流作用下的边坡稳定性分析[J].长江科学院院报，2006，23（4）：13-16.

[7]张鲁渝，郑颖人，赵尚毅，等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报，2003（1）：21-27.

[8]Dawson E M，Roth W H，Drescher A.Slope stability analysis by strength reduction[J].Geotechnique，1999，49（6）：835-840

[9]Lechman J B，Griffiths D V.Analysis of the progression of failure ofearth slopesby finite elements[C]//International Conference of Slope Stability，2000：250-265.