不确定非完整系统的自适应有限时间镇定

李飞祥

（1.郑州大学数学系，郑州 450001；2.安阳师范学院数学与统计学院，河南安阳 455000）

不确定非完整系统的自适应有限时间镇定

李飞祥1，2

（1.郑州大学数学系，郑州 450001；2.安阳师范学院数学与统计学院，河南安阳 455000）

研究了一类具有非线性参数化链式非完整系统自适应有限控制问题.基于参数分离技术，input-state-scaling变换技巧和backstepping设计方法构造连续时变反馈有限时间自适应控制律.通过切换策略有效克服系统在x0(t0)=0不能控的现象，该控制律保证闭环系统同Lyapunov稳定和有限时间收敛.

自适应；有限时间稳定；非完整系统；非线性参数化

近几年来，非完整系统的控制问题引起了广泛关注.这些已有结果大多是通过时变或非光滑状态反馈控制律来完成系统的渐近（指数）镇定.由于系统在复杂的工作环境中，受各种干扰因素的影响，具有不确定性是不可避免的.本文研究了一类具有非线性参数化的链式非完整系统的有限时间镇定问题.通过参数分离技术解决了参数的非线性化问题，并通过input-state-scaling[1]和backstepping[2]技术显示设计状态反馈控制器.

1 问题描述

本文考虑如下一类不确定链式非完整系统

其中(x0,x)=(x0,x1,…,xn)∈Rn+1，(u0,u1)∈R2分别表示系统的状态和控制输入，fi,i=0,1,…,n为其相应变量的连续函数，θ∈Rm为未知参数向量，di为未知虚拟控制系数，fi,i=0,1,…,n为其相应变量的C1函数且满足fi(0,θ)=0.控制目标是设计鲁棒自适应控制器

使闭环系统状态有限时间调节到零点.

为此，在本文中对系统（1）作如下假设：

假设1存在正数ci1和ci2使得ci1≤di≤ci2.

假设2存在非负光滑函数f¯i满足

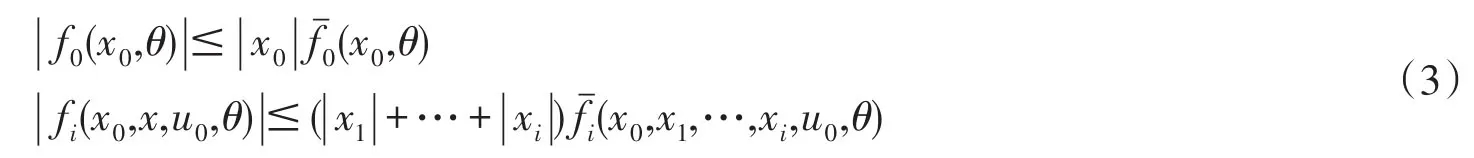
在系统分析之前，我们首先介绍有限时间稳定的概念和一些引理.

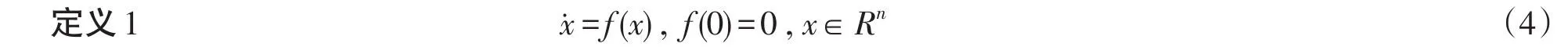
其中f:U0→Rn在包含原点x=0的一个开邻域U0内关于x连续.如果系统的平衡点x=0是Lyapunov稳定，

并且在一个U⊆U0邻域内是有限时间收敛的，则称x=0是局部有限时间稳定的.

引理1对以系统（1）存在光滑函数γ0(x0)≥1和γi(x0,x1,…,xi,u0)≥1使得

其中Θ≥1是一个依赖θ的不确定常数.

引理2[3]对于任意实数xi, i=1,…,n和0＜b＜1，有

当b=p/q＜1,其中p＞0和q＞0都为奇数，则

2 有限时间自适应控制

在这部分我们利用backstepping方法设计系统的自适应有限控制器.首先处理x0(0)≠0，然后再讨论x0(0)≠0的情形.系统的下三角结构蕴含了u0和u1可以分离设计.

2.1 x0(0)≠0时的系统分析

对于x0-子系统，我们设计控制律如下

其中k0是一个正的设计常数，0是Θ第一次估计，选取Lyapunov函数

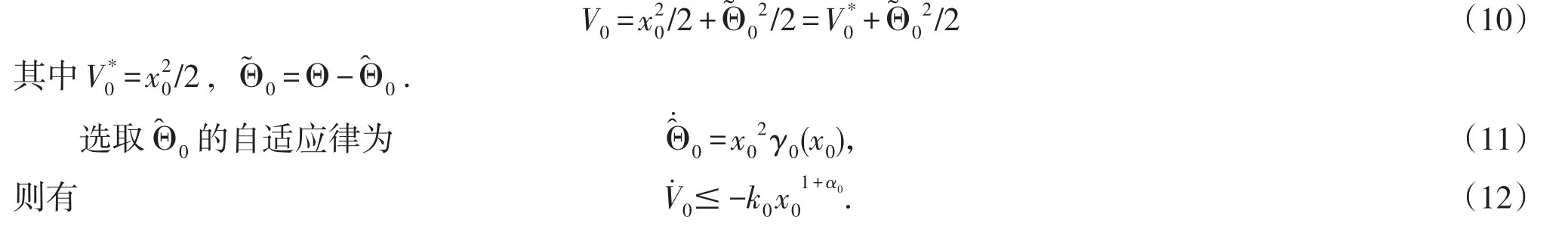
定理1x0-子系统在控制律（8）作用下有限时间自适应稳定.

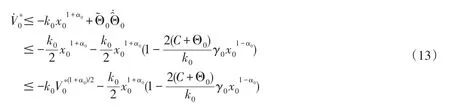
因此，对于任意给定的有限时刻ts＞0，都有x0(ts)≠0，故（8）式中的u0(t)≠0, ∀t≥ts.从而控制设计的input-state-scaling变换能够执行.当t∈[0, ts)时，采用（36）式定义的u0以及产生的新的控制律u1，当t≥ts切换输入u0，u1到（8）,（33），从而得到本文的主要结果.

定理2在假设1-2下，存在状态反馈控制律（8），（33）和自适应律（11）和（34），并应用上述切换控制策略，使不确定非完整系统（1）到状态全局有限时间调节到原点.

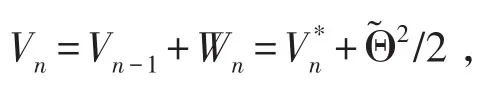
令α=2n/(2n+1)∈(0,1)，则由引理3有

3 结论

本文考虑一类带有非线性参数化链式非完整系统的有限时间自适应镇定问题.基于参数分离技术处理非线性参数，利用input-state-scaling变换技巧和backstepping设计方法，设计自适应控制器.该控制器保证闭环系统同时是Lyapunov稳定和有限时间收敛的.

[1]Astolfi A.Discontinuous control of nonholonomic systems[J].Systems&Control Letters,1996,27:37-45.

[2]Bhat S,Bernstein D.Continuous finite-time stabilization of the translational and rotational double integrators[J].IEEE Trans on Automatic Control,1998,43:678-682.

[3]Jiang Z P.Robust exponential regulation of nonholonomic systems with uncertainties[J].Automatica,2000,36:189-209.

[4]Lin W,Qian C.Adaptive control of nonlinearly parameterized systems:a nonsmooth feedback framework[J].IEEE Trans on Automatic Control,2002,47:757-774.

[5]Hong Y.Finite-time stabilization and stabilizability of a class of controllable systems[J].Systems&Control Letters,2002,46:231-236.

[6]Do K,Pan J.Adaptive global stabilization of nonholonomic systems with strong nonlinear drifts[J].System&Control Letters,2002, 46:195-205.

Adaptive Finite-Time Stabilization of Nonholonomic Systems with Uncertainties

LI Fei-xiang1,2
(1.Department of Mathematics,Zhengzhou University,Zhengzhou 450001,China; 2.School of Mathematics and Statistics,Anyang Normal University,Anyang 455000,China)

In this paper,adaptive finite-time control is presented for a class of uncertain nonholonomic systems in chained form with nonlinear parameterization.Using parameter separation,state scaling and backstepping,an adaptive finite-time control law is obtained in the form of continuous time-invariant feedback.Both Lyapunov stability and finite time convergence are guaranteed by appropriately choosing the design parameters.An adaptive control based switching strategy is used to overcome the uncontrollability problem associated withx0(t0)=0.

adaptive;finite-time stability;nonholonomic systems;input-state-scaling;nonlinear parameterization

O231

A

1008-2794（2011）10-0048-05

2011-09-02

国家自然科学基金（61073065）；河南省教育科学“十二五”规划资助项目（[2011]-JKGHAD-0199）.

李飞祥（1981—），男，河南洛阳人，安阳师范学院数学与统计学院讲师，硕士，研究方向：基础数学.