原子与耦合腔相互作用系统中原子布居数的演化
吴亚女
原子与耦合腔相互作用系统中原子布居数的演化
吴亚女
(漳州工业学校,福建 漳州 363000)
研究两个二能级原子分别与耦合腔A和B相互作用系统中原子布居差随时间演化规律。讨论腔场间的耦合强度变化对原子布居差演化的影响。研究结果表明:随腔场间耦合强度的增强,原子布居差随时间演化的行为经历从不规则振荡到呈现周期性振荡的过程。当腔场间耦合强度较弱时,原子布居差随时间演化呈现崩塌和恢复效应。当腔场间耦合强度较强时,原子布居差呈现周期性演化规律。
量子光学;二能级原子;耦合腔;原子布居数
1 引言
原子与光场相互作用系统中光场和原子的量子特性的研究一直是量子光学研究的热点。至今,人们已利用J-C模型对光场与原子相互作用系统的量子特性作出了大量的研究。如原子布居的崩塌和回复效应[1],原子算符的偶极压缩[2-5],光场的压缩特性和反聚束效应[6]等。另一方面,腔QED技术和囚禁离子技术是实现多比特纠缠态、量子信息处理和量子计算等最有前途的技术。1995年Kimble小组利用腔QED技术实验上第一次演示并测量了与量子逻辑门有关的相移[7]。近十多年来,法国Haroche领导的ENS小组利用腔QED技术在实验上成功实现两原子EPR纠缠态[8]、两腔模的EPR纠缠态[9]、三粒子GHZ态[10]和两比特量子逻辑门[11]等。近年来,人们还提出了许多利用QED技术进行量子态制备和传送的方案[11,12]。但在以往利用原子与腔场相互作用系统中,大多集中在原子与非耦合腔相互作用的情况。最近十年来,原子与耦合腔相互作用系统引起了人们极大的关注。例如,Zheng等人提出一种利用原子与耦合腔相互作用系统产生双模压缩态的方案[13]。Yang等人提出利用原子与耦合腔相互作用系统实现量子相位门的方案[14]。本文研究了两个二能级原子分别与耦合腔A和B共振相互作用的情况,讨论了系统总激发数为1时,原子布居差演化。
2 系统态矢演化
我们研究如图1所示的系统。两个二能级原子1和原子2通过单光子跃迁分别与耦合腔A和B发生共振相互作用。在旋波近似下,在相互作用表象中系统的哈密顿为

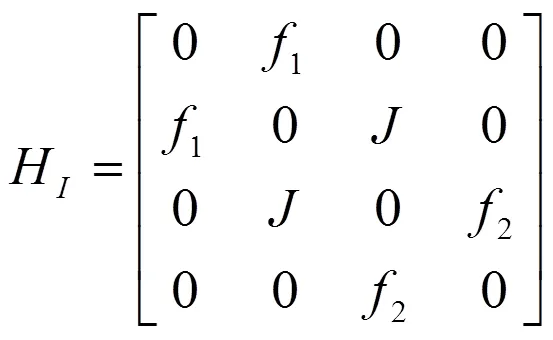

3 原子布居差的演化

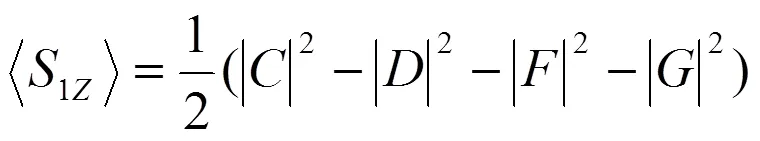

4 结论
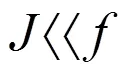

图2 原子1布居差随时间的演化
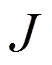
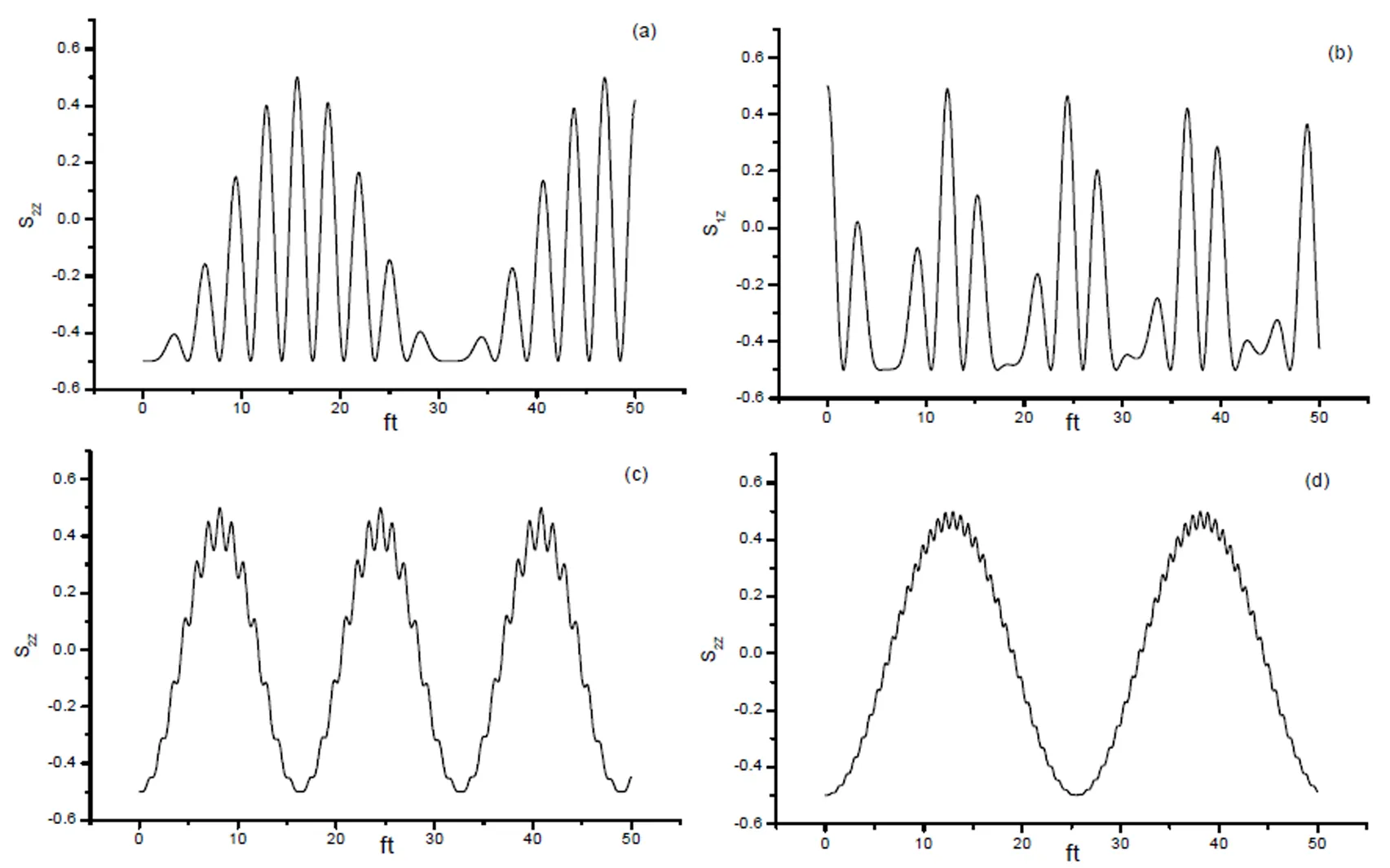
图3 原子2布居差随时间的演化
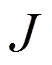
[1] Zhou P,Hu Z.L,Peng J.S. Effect of atomic coherence on the collapses and revivals in some generalized Jaynes-Cummings models[J]. J Mod Opt.,1992,39(1):39-62.
[2] 郭红,彭金生.双模Jaynes-Cummings模型中原子偶极压缩与双模光场压缩间的关联[J].光学学报,1998,18(2):135-140.
[3] 詹佑邦.非共振双光子Jaynes-Cummings模型中原子的偶极压缩[J].物理学报,1994,43(6):895-903.
[4] 周鹏,彭金生.双光子Jaynes-Cummings模型中原子的压缩效应[J].物理学报,1989,38:2044-2048.
[5] 田永红,徐大海,彭金生.级联三能级原子的偶极振幅平方压缩[J].量子电子学报,2001,18(1):334-339.
[6] 王晓光,于荣金,于桦.依赖于时间的Jaynes-Cummings模型中的反聚束效应[J].光子学报,1998,27(4):304-308.
[7] Turchette Q A, Hood C J, Lange W, et.al. Measurement of conditional phase shifts for quantum logic[J].Phys. Rev. Lett. 1995, 75(25): 4710-4713.
[8] Hagley E, Maitre X, Nogues G, et.al. Generation of Einstein-Podolsky-Rosen pairs of atoms [J].Phys. Rev. Lett, 1997, 79(1): 1-5.
[9] Osnaghi S, Bertet P, Auffeves A, et.al. Coherent control of an atomic collision in a cavity [J]. Phys. Rev. Lett., 2001, 87(3): 037902.
[10] Rauschenbeutel A, Nogues G, Osnaghi S, et.al. Step by step engineered many particle entanglement [J]. Science, 2000, 288: 2024-2028.
[11] [11] Rauschenbeutel A, Nogues G, Osnaghi S, et.al. Coherent operation of a tunable quantum phase gate in cavity QED [J]. Phys. Rev. Lett., 1999, 83(24): 5166-5169.
[12] 杨洪钦,谢树森,陆祖康等. 利用三粒子W态隐形传送三粒子GHZ态. 光学学报, 2006, 26(2): 300-304.
[13] Zheng S B, Yang Z B, Xia Y. Generation of two-mode squeezed states for two separated atomic ensembles via coupled cavities [J].Phys. Rev. A ., 2010, 81: 015804.
[14] Yang Z B, Xia Y, Zheng S B. Resonant scheme for realizing quantum phase gates for two separate atoms via coupled cavities [J]. Optics Communications, 2010, 283: 3052-3057.
The evolution of the atom’s occupancy in the system of atoms interacting with coupled cavities
WU Ya-n ü
(Department of Electronic Engineering, Zhangzhou Industrial School, 363000, Zhangzhou, China )
We study the one-excitation dynamics for the system comprising two two-level atoms resonantly interacting with two coupled cavities. The evolution of the atom’s occupancy is investigated. The influences of coupling constant between cavities on the evolution of the atom’s occupancy are discussed. The results obtained show that the evolution of the atom’s occupancy displays collapse and revival effect when the coupling constant between cavities is much smaller than coupling constant between atom and cavity, and it displays periodicity when the coupling constant between cavities is much larger than coupling constant between atom and cavity.
quantum optics; two-level atom; coupling cavities; atom’s occupancy
O431.2
A
1673-1417(2011)02-0066-05
2011-04-10
吴亚女(1971-),女,福建诏安人,中学一级教师,本科。
(责任编辑:季平)

