相位噪声对PSK系统性能的影响

黄 慰

(中国西南电子技术研究所,成都 610036)

1 引 言

由于相移键控(PSK)调制具有恒包络特性,频带利用率比频移键控(FSK)调制高,并且在相同的信噪比条件下,误码率也比FSK调制低,同时PSK调制和解调方式的实现方法也比较简单。因此,以BPSK(二相相移键控)和QPSK(四相相移键控)为代表的PSK调制方式以其抗干扰性能强、误码率低、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统中。但是,随着PSK相位点数的增加,其对相位噪声的敏感程度也相应增加。

本文介绍了相位噪声的定义,阐述了在接收系统中的相位噪声对PSK系统误码率的影响,并以QPSK调制方式为例,进行了接收机本振信号源不同参数变量的相位噪声对系统误码率的仿真分析,推导出本振源相位噪声对QPSK系统误码率的影响,仿真结果证明了接收系统中本振信号源相位噪声的重要性。同时,以实际工程中使用的本振信号源为例,计算了相位噪声和信号抖动所导致的BPSK和QPSK接收系统信噪比的限制。

2 接收机相位噪声的定义

一般来说,所有超外差接收机都会使用一个或者多个本振信号源在解调之前把输入射频信号变换为中频信号,其原理如图1所示。

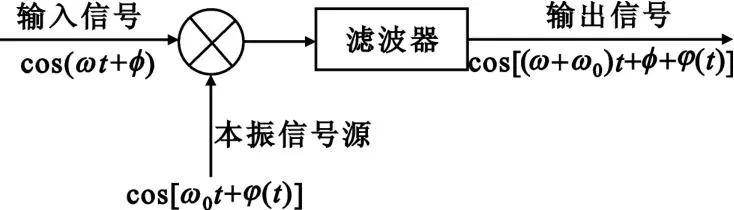
图1 频率变换时本振相位噪声的影响Fig.1 The effect of LO phase noise in frequency transform

在理想接收机中,本振信号源是一个纯净信号,在频域,其为一根谱线;在时域,其正弦波的周期为一个恒定值。它们在混频器中进行频率变换时,不会使输出信号产生畸变,所有的信息都能被恢复出来。但在实际中,本振信号源不可能绝对纯净,总会受到各种噪声的调制而产生调制边带,本振信号源会使输出的信号产生畸变,从而降低系统的解调性能。本振信号源对信号的恶化,主要表现为随机相位抖动,也就是通常说的相位噪声[1]。这样,任何一个输入信号经过本振信号源下变频后的输出信号都会带有随机相位噪声。

接收系统的相位噪声实际上专指本振信号源的相位噪声,而本振的相位噪声是衡量其短期稳定度的一个技术指标。相位噪声早期也称为相位抖动,在时域多用阿伦方差表示,在频域多用相位噪声表示,用偏离载波某个频偏处的单位带宽(1 Hz)内的相位噪声功率谱密度来表示,单位为dBc/Hz[2]。

本振信号源输出的伴有随机相位干扰的载波信号可以表示为

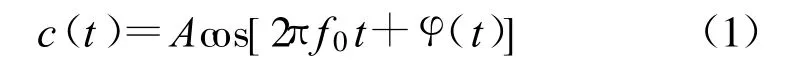
式中,A为信号幅度,f0为载波频率,φ(t)为随机的相位干扰,即相位噪声。在电子系统中,热噪声及相关噪声一般是具有零均值正态分布的平稳随机过程,在频域中可用功率谱密度表示。一般相位噪声φ(t)的功率谱密度函数可以表示为

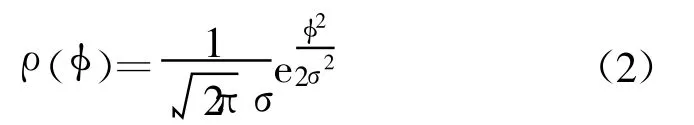
3 相位噪声对PSK系统误码率的影响

通信系统中本振信号源的相位噪声是一项非常重要的性能指标,它对通信设备和系统的性能会产生很大的影响。对于PSK系统,相位噪声的干扰常会引起星座点的旋转、扩散和模糊。本振信号源的相位噪声在解调过程中会和有用信号一起出现在解调终端,引起基带信号的信噪比下降,系统误码率增加;同时,由于接收机本振信号源存在相位噪声,当接收机遇到强干扰信号时,还会产生“倒易混频”现象,使得输出端噪声加大,系统信噪比降低[3]。

在通信系统中,误比特率(Bit Error Rate,BER)或误码率是指接收系统错误解调出信号的概率,即信息S1被发射,接收系统误认为是S2。通过概率统计原理,这个事件的发生概率为

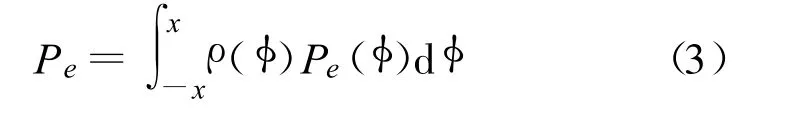
因此,本振相位噪声对通信系统误码率的计算方法为

由于调制方式不同,在不同相位噪声影响下,其系统的误比特率也不同,在文献[4-6]中介绍了不同调制样式下系统误码率的表达式。现以PSK系统中最常见的两种调制方式为例,将其各自系统的误码率表达式列出来,其在相位噪声为 的情况下的系统误码率表达式见表1。

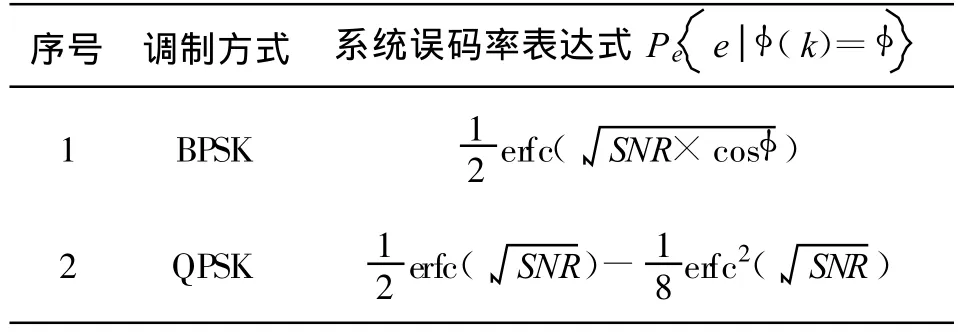
表1 在相位噪声为 时不同调制方式的系统误码率表达式Table 1 The expression of BER in different modulation systems with phase noise

表1中,SNR为输入信号的信噪比值;erfc(Complementary Error Function)为补余误差函数,该函数为通信系统中一个常用函数,其定义为

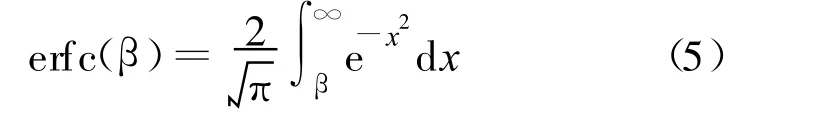
以QPSK调制方式为例,参照公式(2)、(4)以及表1的内容,假设接收机本振的相位噪声是非相关的,且具有正态分布,利用Matlab工具,进行了不同变量参数条件下的相位噪声对QPSK接收系统误码率影响的仿真,其结果如图2所示。

图2 不同变量参数的相位噪声对QPSK系统误码率的影响Fig.2 The BER performance of QPSK modulation with different phase noise variance

从图2的仿真结果中可以看出,在相同信噪比条件下,随着相位噪声方差(σ)值的增大,系统误码率(BER)也随之升高,即相位噪声越大,系统的误码率越大;同时,当误码率一定时,随着相位噪声的增大,对系统信噪比也提出了更高的要求。经过定量分析可以得出,在QPSK系统中,当误码率为1×10-4时,本振的相位方差 σ分别为0.005、0.008和0.012时,系统的信噪比也只有相应增加0.6dB、1.3dB和2.1dB才能满足误码率的要求。

4 相位噪声对实际PSK系统影响的分析

在实际工程中,对接收系统相位噪声的描述,往往不会使用本振信号源的相位方差值(σ)来表示,该值一般是在理论分析时采用。在实际中,相位噪声通常定义为在某一给定偏移频率处的噪声功率谱密度,其单位为dBc/Hz,dBc是以dB为单位的该频率处功率与总功率的比值。中心频率的功率并不重要,因为抖动只反映了相位噪声(即调制)与“纯”中心频率处的相对功率值。

现以一个实际工程的C频段本振信号源的相位噪声为例进行分析,该信号源的相位噪声值的定义如表2所示。

表2 本振信号源的相位噪声值Table 2 The phase noise of local oscillator

通过第2节的介绍可知,相位噪声表征的是信号频率的稳定度,在频域上就是噪声边带,也就是相位噪声;在时域上与之对应的叫做信号的抖动,相位噪声和抖动是对同一种现象的两种不同的定义方式。因此,如果能从相位噪声的测量结果中导出信号抖动的值将是有意义的。

相位噪声值与信号抖动之间的转换公式为

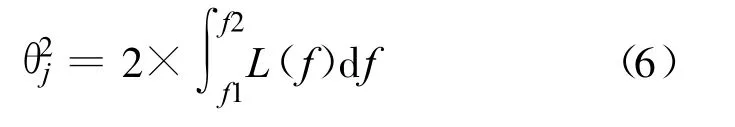
式中,θj是信号的抖动,L(f)是相位噪声的功率谱密度值的表达式,f1为该相位噪声值的频率下限,f2为该相位噪声值的频率上限。该公式计算出的值为弧度(rad),可通过公式(7)将其转化为以角度为量纲的信号抖动值:

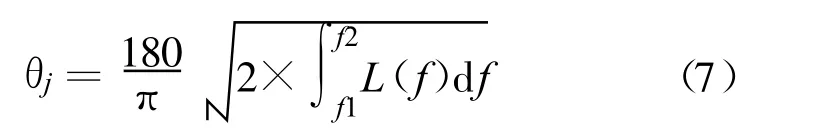
以表2中本振信号源的相位噪声值数据为例,对各自频偏的相位噪声进行分段线性积分,按照公式(7)计算得到各级相位噪声引起的信号抖动和总的信号跳变度数见表3。

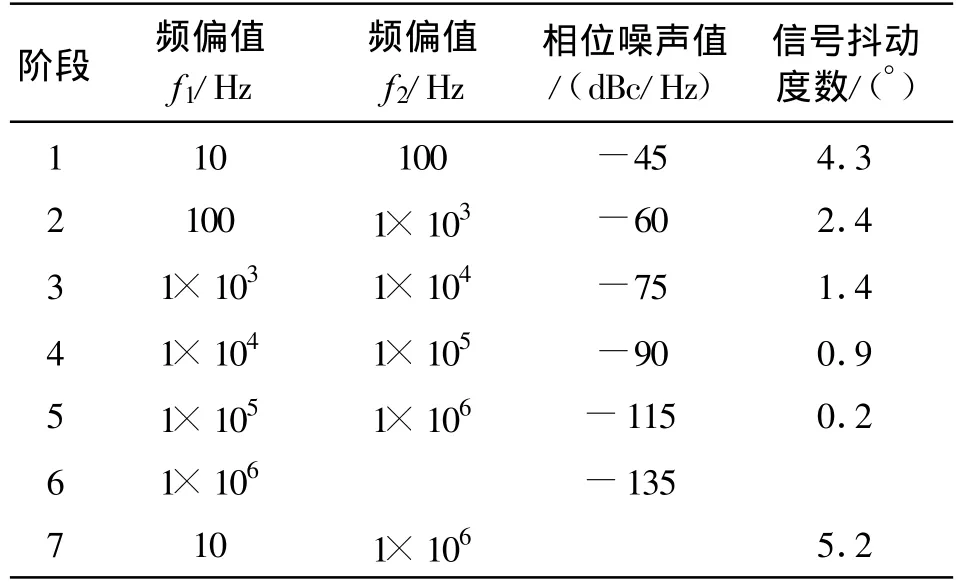
表3 相位噪声引起的信号跳变度数Table 3 The phase noise induced jitter

对于一个BPSK系统中,信息被±180°的相位变化所承载,在±90°判决点会发生一个错误。上例中本振信号源引起的信号跳变为5.2°,在实际接收系统里意味着,接收机固有的相位跳变会导致信号越过边界,那么就会产生错误。对于一个BPSK信号,5.2°在90°的判决中所占比例为5.8%,则该接收机将会削减判决区域5.8%,所能达到的最大信噪比为

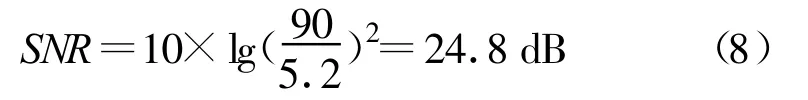
同理,该本振信号源接收系统对于QPSK调制信号,5.2°的信号跳变会导致判决区域减少11%,能达到的最大信噪比为18.7dB。

在常用PSK系统中,BPSK的相位偏移是180°的整数倍,QPSK的相位偏移是90°的整数倍,8PSK的相位偏移是45°的整数倍。工程经验表明,对于一个特定的相移键控系统,当系统误码率大于10-6,如果本振的寄生调相小于该相移键控最小相位步进的十分之一时,系统的误码率与理论值的差异仅在几分贝之内。根据这个经验,BPSK系统的寄生调相应小于18°,QPSK系统的寄生调相应小于9°,8PSK系统的寄生调相应小于4.5°。

所以,在上例中寄生调相为5.2°的C频段的本振信号源只能用在 BPSK和QPSK系统中,对于8PSK系统,该本振信号源会引起系统误码率增加,且至少大于10-6。

通过上述介绍的预测法,结合系统的调制方式,能够对PSK接收系统本振信号源的指标提出更加合理的要求,即不要只顾接收系统的噪声系数而忽略了本振信号源,把该信号源相位噪声的指标提得过低,从而影响整个系统的解调误码率和接收灵敏度;也不要脱离工程实际,把本振信号源的指标提得过分苛刻、过于严格,人为地增加系统的设计难度和成本。

5 结 论

本文介绍了相位噪声的定义及其对PSK系统误码率的影响,并结合接收系统本振信号源不同变量参数的相位噪声对QPSK调制方式误码率的影响进行了仿真。通过仿真分析得到,接收系统本振源的相位噪声越大,系统的误码率越高,证明了接收系统中本振信号源相位噪声的重要性。同时,以实际工程中使用的本振信号源为例,计算了相位噪声和信号抖动对BPSK和QPSK接收系统信噪比的限制。

理论分析与工程实践的相结合,更好地得出了相位噪声对PSK接收系统的影响,对接收系统的工程设计具有一定的指导意义。

[1] 高树廷,刘洪升.相位噪声分析及对电路系统的影响[J].火控雷达技术,2003(6):58-63.GAO Shu-ting,LIU Hong-sheng.Analysis of Phase Noise and Its Effects on Circuit Systems[J].Fire Control Radar Technology,2003(6):58-63.(in Chinese)

[2] 贾群.频率合成器的相位噪声分析[J].电子科技,2009(2):40-43.JIA Qun.Analysis of Phase Noise in the Frequency Synthesizer[J].Electronic Science and Technology,2009(2):40-43.(in Chinese)

[3] 柴菁,张文军,管云峰.相位噪声对QAM系统的影响及消除方法分析[J].电视技术,2008,48(4):54-57.CHAI Jing,ZHANG Wen-jun,GUAN Yun-feng.Analysis of the Effect and Compensation Method of Phase Noise in QAM System[J].Video Engineering,2006,48(4):54-57.(in Chinese)

[4] Mahboob Iqbal,Jeongseon Lee,Kiseon Kim.Performance Comparison of Digital Modulation Schemes with Respect to Phase Noise Spectral Shape[J].Electrical and Computer Engineering,2000(3):856-860.

[5] Roberto Corvaja,Silvano Pupolin.Phase Noise Effects in QAM System[C]//Proceedings of the 8th International Symposium on Persional,Indoor and Mobile Radio Communications.Helsinki,Finland:IEEE,1997:452-456.

[6] Prabhu V K.PSK Performance with Imperfect Carrier Phase Recovery[J].IEEE Transactions on Aerospace and Electronic Systems,1976,12(2):275-286.