宽带双频双极化星载赋形反射面天线优化设计

张新刚,吴 刚,钟 鹰

(中国空间技术研究院西安分院,西安 710100)

1 引 言

在新一代的卫星通信系统中不仅要求天线波束与服务区的形状匹配,还需满足大容量通信、收发一体化的要求,以处理同步进行接收与发射的两个分离频段的信号,这要求天线能够同时实现宽带、双频、双极化工作。赋形反射面天线具有结构简单、成本低、损耗小、易实现双频和双极化等诸多优点,在卫星通信系统中应用十分广泛[1]。但要求赋形反射面天线在按照服务区的形状对波束进行赋形的同时实现宽带、双频、双极化特性,具有一定的难度,因为此时对反射面天线的设计是一个多目标优化问题,优化过程中需要在多个优化目标之间进行折衷。目前,国内外现有星载赋形反射面天线的带宽一般为500MHz或800MHz,限制了它在卫星通信领域的应用潜力。

目前,对赋形反射面天线进行优化设计的算法主要有最速下降法[2]、遗传算法[3]、Minimax算法等[4],但在实际工程应用中要求服务区内任意一点的天线增益都要满足设计指标,因此Minimax算法的设计理念最符合实际工程需要。以往在用Minimax算法进行优化时通常是通过各个评估站点的电场来构建目标函数,然而设计要求一般是以增益的形式给出的。直接以各个评估站点的电场来构建目标函数,必然导致同样的增益偏差在增益要求较高的站点引起较大的电场偏差,优化的重点过多地放在了增益要求较高的站点。为了消除各个评估站点增益对优化过程的影响,尽可能拓宽天线带宽,本文采用归一化的电场值来构建目标函数。最后以一个服务区为美国国土、工作在Ku频段宽带双频双极化的单偏置抛物反射面天线为例,在一定增益要求下对其宽带性能进行了优化设计,从而充分说明了本文方法的有效性。

2 天线分析方法

由于反射面天线尺寸相对于工作波长(λ)属于电大尺寸,一般采用PO法进行分析计算[5-6]。反射面天线的远场表达式为

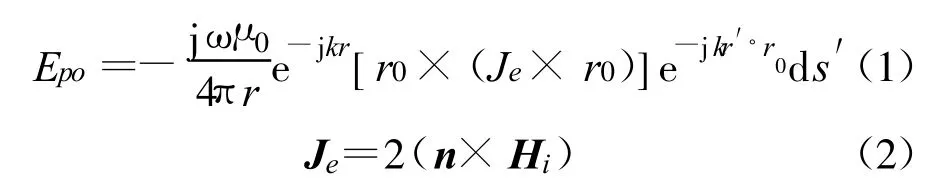
式中,Hi是馈源在反射面上的入射磁场,Je是反射面表面的感生电流,n是反射面上法线的单位矢量,μ0是自由空间的磁导率,ω是角频率,k是波数,k=2π/λ,r是观察点所在的位置矢量,r= r ,r0=r/r,r′是场源所在的位置矢量,S′是反射面表面。

如果要考虑交叉极化增益或者远区旁瓣,PO法的计算精度就不能满足要求,必须把反射面边缘的绕射作用考虑进去。本文采用物理绕射理论[7-8]对PO的计算结果进行修正,以提高计算结果的精度。

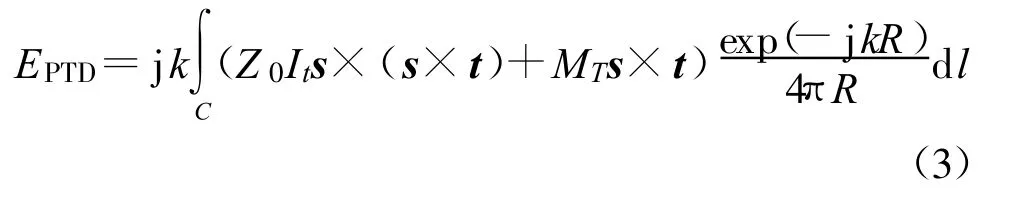
式中,IT和MT分别是反射面边缘等效电流和磁流,s是散射波单位矢量,t是反射面边缘切向单位矢量,R= r-r′ ,Z0是自由空间特征阻抗,C是反射面边缘的闭合曲线。

3 目标函数及优化算法

投影口径为圆形的单偏置反射面天线的结构示意图如图1所示,其中 a是投影面口径的半径,H是偏置距离,f是焦距,θ0是馈源的偏置角。

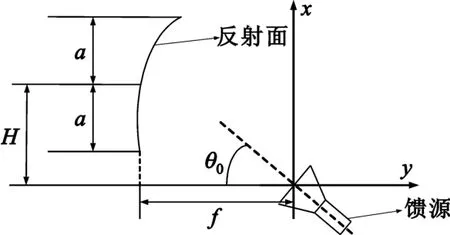
图1 单偏置赋形反射面天线的几何结构Fig.1 Geometry of an offset single-reflector antenna

在如图1所示的坐标系中,反射面可以通过下式表示:

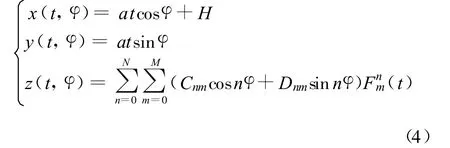
式中,t和φ为在口径投影坐标系下的坐标变量,Cnm和Dnm是反射面的展开系数,Fnm(t)是修正的Jacobi多项式。

在对反射面天线进行优化设计前,a、H、f、θ0以及馈源的具体形式作为基本设计参数已经确定。优化所要进行的工作就是根据具体的设计要求,对由Cnm和Dnm构成的优化变量x进行调节,从而产生一个满足设计要求的赋形波束。其中:

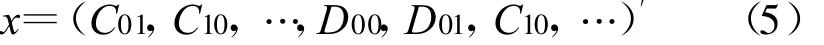
为了保证优化后反射面的形状与标准的单偏置相比不发生太大的形状变化,C00保持不变。

天线服务区域是一个连续的区域,优化时不可能对服务区域内所有位置的性能都进行评估,必须把这个连续的区域离散化,具体的做法是按照一定的规则在服务区域内放置足够多的观测站点[9-10]。

对天线的带宽性能有要求时,优化目标函数中要考虑频率的影响。具体优化计算时,在频带内选择一定数目的频点进行优化,当这些频点的性能满足要求时,就可以认为整个频带内的性能都满足设计要求。当以主极化增益和带宽作为主要评判标准,通常采用下式所示的方式来构建目标函数:

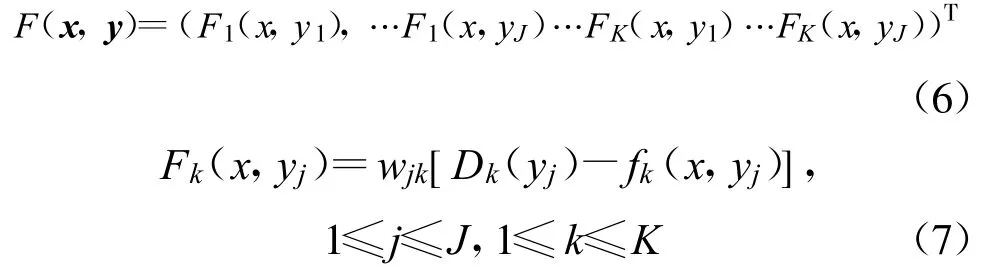
式中,y为在服务区内放置的J个观测站点所形成的观测变量,y=(y1,y2,…,yJ)T;K是优化的频段内所取频点的数目;wjk和Dk(yj)分别是第k个频点时第j个观测站点的权重系数和设计要求的主极化电场值;fk(x,yj)是第 k个频点设计参量为x的情况下第j个观测站点的主极化电场的计算结果。

Minimax方法通过改变参数向量x来使得目标函数F(x,y)的最大值最小化,可以写成如下形式:

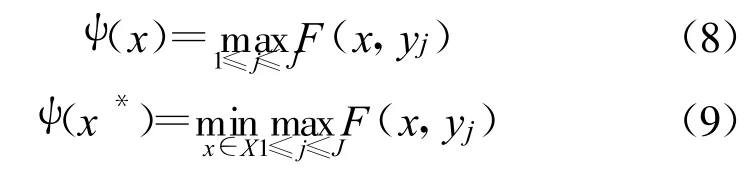
目标函数F(x,y)确定之后,就可以通过合适的算法来寻找其最小点从而使得设计结果满足设计指标要求。但是由于天线的方向性以及实际需求,在工作频带内对各个站点的增益要求是不同的。假定对编号为1和2的两个站点的设计增益分别为G1、G2,优化过程中两个站点的计算增益与设计增益的偏差分别为ΔG1、ΔG2,计算所得的电场值分别为 f1(x)、f2(x),则此时如果采用式(7)所示的方法来建立目标函数,此时两个站点偏差函数的数值比为

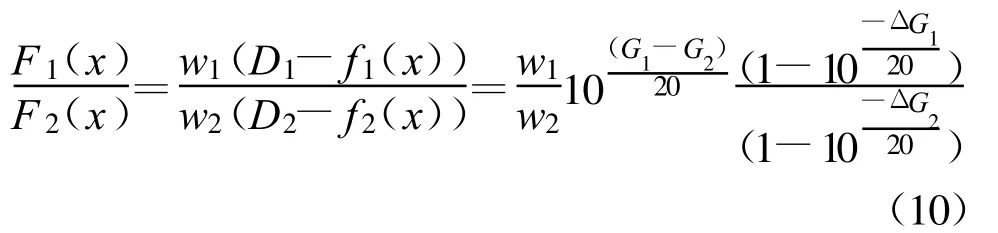
从上式可以看出,偏差函数的数值比不仅与权重系数、增益偏差有关,还与各个站点的设计增益有关;当权重系数和增益偏差相同时,设计增益较高的站点偏差函数的值较大。

Minimax优化算法的核心思想是使所有站点偏差函数的最大值最小化,因此优化时把优化重点放在偏差函数值较大的那些站点。采用式(7)所示的方法来建立目标函数,站点的设计增益对其偏差函数的数值存在正比的影响,优化重点将放在增益较高的站点,必然会影响到优化进行的方向。Minimax算法是一种局部搜索迭代算法,优化过程中不同的进行方向可能导致不同的结果。为了使优化结果尽可能地靠近全局最优解,本文采用归一化的电场来构建目标函数,具体形式如下式所示:

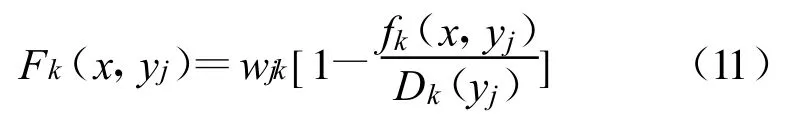
如果采用式(11)所示的方法来建立目标函数,此时1和2两个站点的偏差函数值之比为

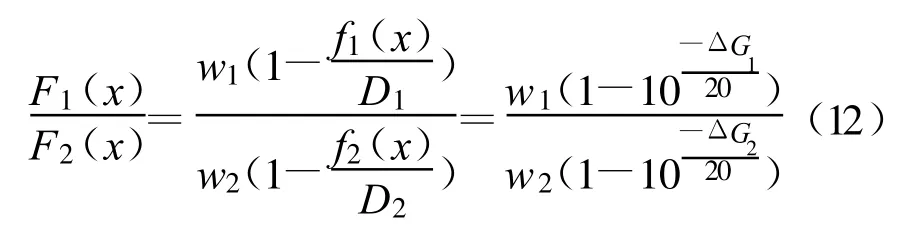
从上式可以看出,偏差函数的值仅与权重系数、增益偏差有关;在权重系数相同的条件下,同样的目标函数值在不同的站点引起的增益偏差是相同的,消除了各站点不同的设计增益对目标函数的影响,有利于获得更好的优化结果。

4 仿真实例及结果

下面通过对一个工作在Ku频段宽带的单偏置抛物反射面进行优化设计来说明算法的有效性。天线的服务区域为美国国土,具体形状如图2所示。图中小黑点是优化过程中部分观测站点位置,阴影区域是降雨量较大的区域,图中的坐标有±0.1°的误差[11]。

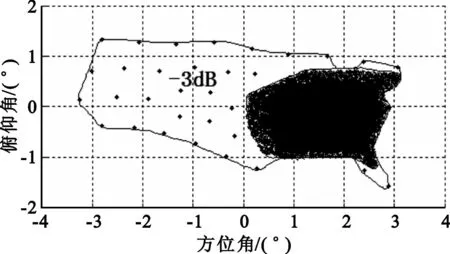
图2 服务区形状示意图Fig.2 Sketch map of the coverage area

具体设计要求是:天线上、下行的带宽都要达到1000MHz;工作频段为 :上行 13.75～ 14.75GHz,下行11.45～12.45GHz;上行为 y极化,下行为 x极化。在整个频段内,服务区的上行增益为30dBi(允许服务区边界区域降低0.5dB);下行增益为29dBi(允许服务区边界区域降低0.5dB);为补偿雨衰引起的信号衰减,阴影区的下行增益需要加强3dB,达到32dBi。

进行优化设计时,天线选用单偏置抛物反射面天线,具体结构形式如图1所示,其中a为0.762 m,f为1.506 m,H 为1.245 m,θ0为 42.77°。馈源为双极化的(cosθ)q式馈源,q=14.28。优化时 N=9,M=5,优化变量的个数为89(不含C00)。

当设计要求和基本参数确定后,通过自编的Matlab程序来进行优化设计。当采用式(7)的方式来构建目标函数时,优化后服务区边缘的电场值不能在要求频带内达到设计指标要求。采用式(11)的方式来构建目标函数时,优化后得到的远场等值线图如图3和图4所示。其中,图3为在下行频段的远场方向图,图4为上行频段内的远场方向图。图中的“×”点与图2中黑点是对应的,表示观察站点的位置,外围的“×”点代表国土地边界。

从图中可以看出,在11.45～12.45GHz下行频带内,服务区内任意一点的增益都在29dBi以上,并且在95%以上的服务区域内都高于30dBi,阴影区域的增益都在32dBi以上;在13.75～14.75GHz上行频带内,服务区内任意一点的增益都在30dBi以上;天线的上、下行带宽都为1000MHz,具有良好的宽带性能。

图3 优化后得到的下行频段远场方向图Fig.3 Contoured patterns in downlink band of the optimized antenna

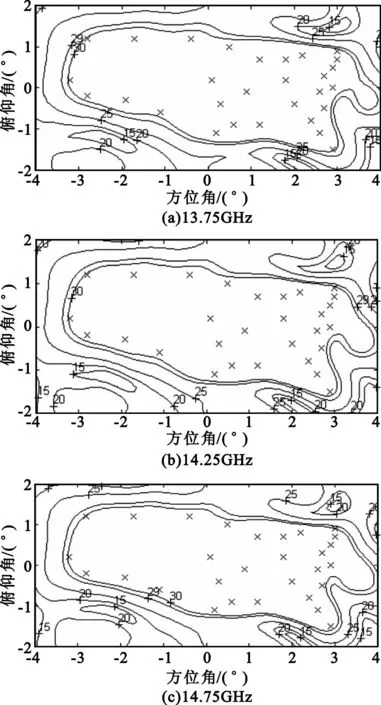
图4 优化后得到的上行频段远场方向图Fig.4 Contoured patterns in uplink band of the optimized antenna

优化后反射面相对于标准单偏置抛物面形变量的等值线图如图5所示。从图中可以看出优化后反射面形变量在(-0.7λ,0.6λ)范围内,且没有发生突变的区域,整个表面比较光滑,满足实际加工要求。

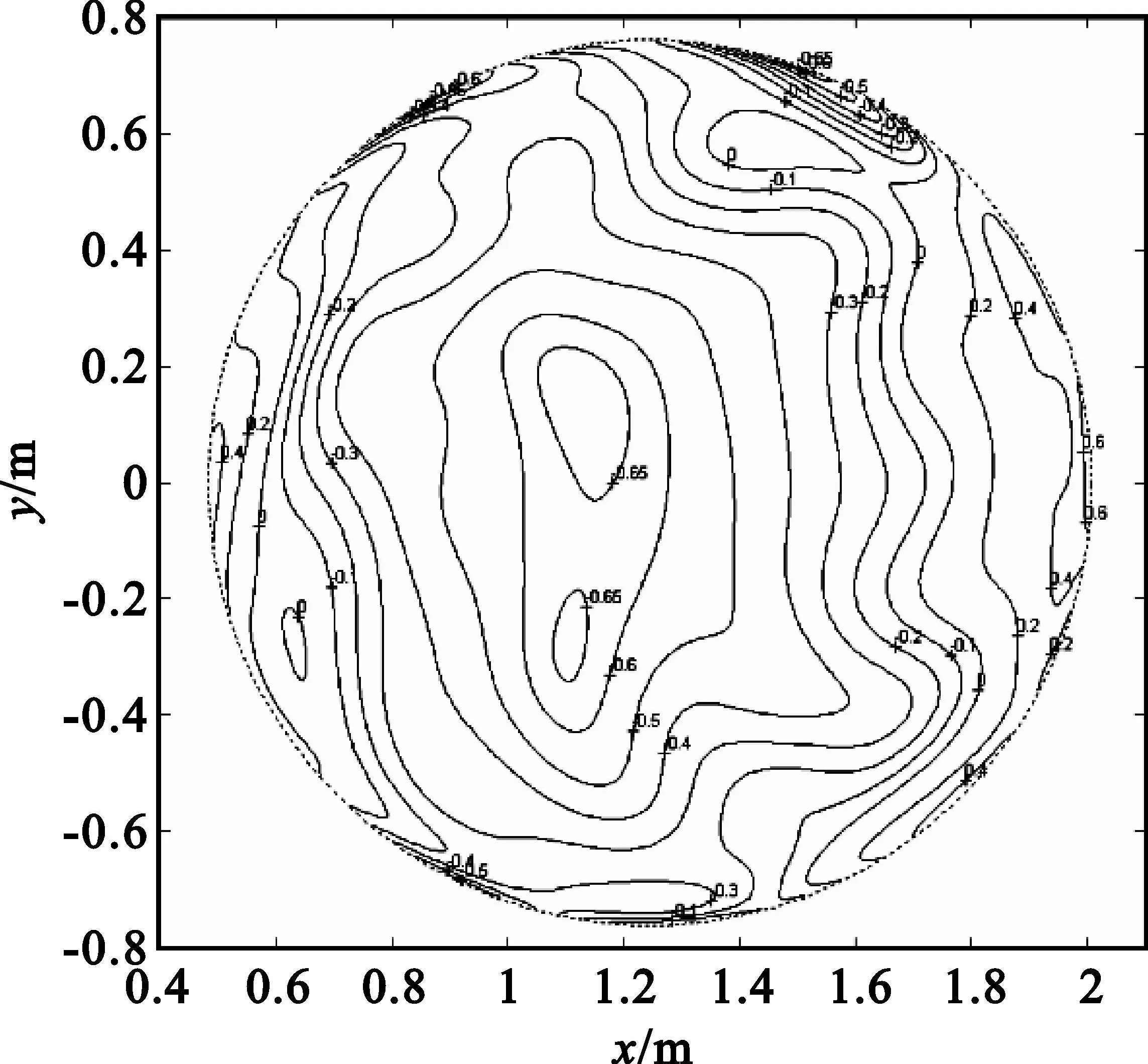
图5 优化后反射面形变量等值线图(单位:λ)Fig.5 Contoured patterns of the deviation in z direction

5 结 论

本文在用Minimax算法对赋形反射面天线带宽性能进行优化设计过程中,采用归一化的电场值来构建目标函数,消除了设计增益对优化过程的影响,有效地拓宽了天线的带宽。从对实际工程设计实例的仿真结果可以看出,在满足服务区特定增益要求的前提下,赋形反射面天线的上、下行频带的带宽都达到了1000MHz,比实际应用中的同频段天线带宽至少提高了200MHz,具有良好的宽带性能;并且优化得到的反射面表面比较光滑,满足实际加工要求。优化结果对工程应用具有重要的参考价值,为将来更宽的Ka频段天线优化设计奠定了基础。

[1] Roederer A G,Jensen N E,Crone G A E.Some European satellite-antenna developments and trends[J].IEEEAntennas and Propagation Magazine,1996,38(2):9-21.

[2] Chou H,Chou H T.Fast SDM for shaped reflector antenna synthesis via patch decompositions in PO integrals[J].Progress in Electromagnetic Research,2009,92:361-375.

[3] Acila S L,Carpes W P,Vasconcelos JA.Optimization of an offset Reflector Antenna Using Genetic Algorithms[J].IEEE Transactions on Magnetics,2004,40(2):1256-1259.

[4] Klein C.Design of shaped-beam antennas through minimax gain optimization[J].IEEE Transactions on Antennas and Propagation,1984,32(9):963-968.

[5] 李鹏,张志华,王为,等.基于不同网格形式的反射面天线方向图分析[J].系统工程与电子技术,2009,31(2):347-351.LI Peng,ZHANG Zhi-hua,WANG Wei,et al.Far field pattern numerical analysis of reflector antenna based on different grid forms[J].Systems Engineering and Electronics,2009,31(2):347-351.(in Chinese)

[6] 王伟,段宝岩,马伯渊.重力作用下天线反射面形变及其调整角度的确定[J].电波科学学报,2008,23(4):645-650.WANG Wei,DUAN Bao-yan,MA Bo-yuan.Gravity deformation and best rigging angle for surface adjustment of large reflector antennas[J].Chinese Journal of Radio Science,2008,23(4):645-650.(in Chinese)

[7] Johansen P M.Uniform physical theory of diffraction equivalent edge currents for truncated wedge strips[J],IEEE Transactions on Antennas Propagation,1996,44(7):989-995.

[8] 肖疆,徐晓文,董涛.多孔毁伤时赋形反射面天线辐射特性的研究[J].电波科学学报,2003,18(6):648-651.XIAO Jiang,XU Xiao-wen,DONG Tao.Study on the radiation characteristics of a shaped beam reflector antenna under the multi-hole damnification[J].Chinese Journal of Radio Science,2003,18(6):648-651.(in Chinese)

[9] Merad,Bendimerad F,Meriah S.Design of linear antenna arrays for side lobe reduction using the tabu search method[J].The International Arab Journal of Information Technology,2008,5(3):219-222.

[10] Phjlara D A.Improving the beam efficiency of an offset parabolic reflector antenna for space-borne radiometric application[J].Progress In Electromagnetic Research C,2009,10:143-150.

[11] Duan D W.A generalized diffraction synthesis technique for high performance reflector antenna[J].IEEE Transactions on Antennas and Propagation,1995,43(1):27-39.