测向交叉定位技术

汪珺

(西安电子科技大学电子工程学院，陕西西安710071)

在电子支援(ESM)系统中，通过对辐射源的电磁参数、方向角和到达时间的被动测量估算辐射源及其载体平台的位置，称为无源定位。由于ESM系统本身不发射能量，仅通过被动测量来对目标进行定位和隐蔽跟踪，这对提高系统在现代电子战(EW)环境下的生存能力具有重要作用。测向交叉定位利用在不同位置处的多个侦察站，根据所测得同一辐射源的方向，进行波束交叉，确定辐射源的位置［1］。对于真实目标来说，一般情况下，方向角度变化慢且范围小，是可靠的辐射源参数之一，特别在现代密集复杂信号环境下，方向参数几乎成为惟一可靠的辐射源参数，且用方向角来定位时对各侦察平台之间的时间统一性要求较低。从这个意义上讲，对方向测量定位方法的研究具有重要的意义。

1 测向交叉定位

1．1 定位原理

设n个位置不同的观测站对同一个辐射源进行交叉定位，如图1所示。n个观测站的坐标分别为(xi，yi)(i=1，2，…，n)，参考方向与y轴一致，利用观测站位置和测向结果建立方程组。文中主要讨论双站测向交叉定位，即n=2时的情况

图1 测向交叉定位示意图

由式(1)可得

在n个观测站的情况下，式(2)可用式(3)的简化形式表示

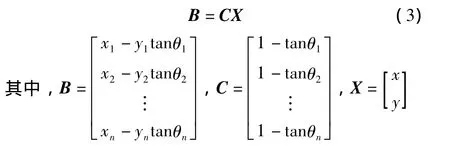
所以，辐射源在平面上的位置坐标为

1．2 定位误差与测量误差的关系

假设各测量误差是零均值、彼此不相关的高斯白噪声，且对应于方位角及站址误差的标准差分别为σθ和σp。在本文分析过程中，一般假设观测误差区最大值，因此标准差恒定。对式(1)求微分，得到定位误差方程

其中，

在n个观测站的情况下，上述方程组可用如下的简化形式表示

由伪逆法解得定位误差估计值为

其中，Z=(FTF)－1FT。

由式(8)可知辐射源定位误差dX=［dxdy］T与方位角测量误差dV、站址各分站的测量误差dXp有关。假设每个观测站的测量结果均相互独立，各测量误差均为零均值且不相关的高斯白噪声，方位角观测误差的方差为，站址各分站的测量误差之间以及与其他测量误差之间相互独立，具有相同的方差。

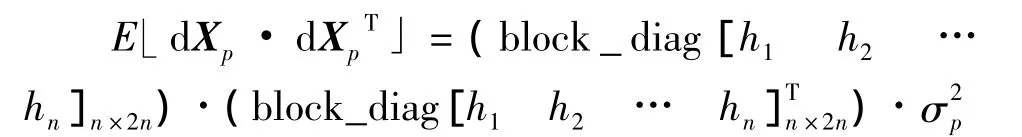
定位误差的协方差矩阵

2 仿真实验及结果分析

采用相对误差表达式，根据测向定位原理及GDOP分布图可以得出，误差最小的定位方向应位于基线的法方向。假设采取沿着x轴且对称原点的基站排放方式，那么辐射源在y轴上运动时，即辐射源到两基站的位置相等时(rA=rB)定位误差最小，综合可得表达式并进行相对误差的仿真。以下仿真图是根据以上述公式的计算结果绘制出的某时刻(n→方向为y轴正向)的GDOP分布图及相对误差曲线图。

2．1 测向精度对定位精度的影响

具体仿真条件为:观测站1坐标为(x1，y1)=(0 km，0 km)，观测站2坐标为(x2，y2)=(30 km，0 km)，站点位置精度为σp=10 m，观测区域在x、y方向均为－400～400 km。

图2绘制了测向误差分别为σθ=3 mrad、σθ=10 mrad、σθ=30 mrad时的定位精度分布图。从图中可以看出:随着测向误差增大，定位误差明显增大，定位精度明显下降，测向误差对定位精度产生了主要的影响，且定位精度的大小和测向精度的大小近似呈线性关系。

图2 测向精度σθ单独作用对定位精度的影响

图3分别为σθ=3 mrad、σθ=10 mrad、σθ=30 mrad时的相对误差曲线图。具体仿真条件为:观测站1坐标为(x1，y1)=(－15 km，0 km)，观测站2坐标为(x2，y2)=(15 km，0 km)，站点位置精度为σp=10 m。

图3 σθ对相对误差的影响

图3绘制了测向精度σθ对相对误差影响的曲线图。总体来看，当辐射源与两个基站的距离超过25 km后，随着距离的增加，相对误差均呈现增长趋势且测向精度越精准，相对误差越小。当σθ=3 mrad时，相对误差较小，定位精度在作用范围内优良;到了σθ=10 mrad时误差增大，定位精度在超过200 km时达不到合格水平;当σφ=30 mrad时误差急剧增大，定位精度已经严重下降，仅在60 km内能达到合格水平。在配置允许范围内尽可能提高测向精度的准确性，这也能够看出测向精度对测向定位的精度有重要影响。

2．2 站点位置精度对定位精度的影响

具体仿真条件:观测站1坐标(x1，y1)=(0，0);观测站2坐标为(x2，y2)=(0，60);测向精度为σθ=3 mrad;观测区域在x、y方向均为－400～400 km。

图4绘制了站点位置精度分别为σp=10 m、σp=100 m、σp=300 m时的定位精度分布图。从图中可以看出站点位置精度对定位精度的影响不大。

图4 站点位置精度σp单独作用对定位精度的影响

图5分别为σp=10 m、σp=100 m、σp=300 m时的相对误差曲线图。具体仿真条件为:观测站1坐标为(x1，y1)=(－15，0)，观测站2坐标为(x2，y2)=(15，0)，测向精度为σθ=3 mrad。

图5 σp对相对误差的影响

图5绘制了站点位置精度σp对相对误差影响的曲线图。总体来看，当辐射源与两个基站的距离超过25 km后，随着距离的增加，相对误差均呈现增长趋势且站点位置精度σp的改变对相对误差影响不大。当站点位置精度σp分别取10 m、100 m、300 m时，定位精度在200 km内能达到优秀水平，在整个作用范围内能达到优良水平。在配置允许范围内尽可能提高测向精度的精准度，这也能够看出测向精度对于测向定位的精度有重要影响。

2．3 基线长度对定位精度的影响

具体仿真条件为:测向精度σθ=3 mrad，站点位置精度σp=10 m，观测区域在x、y方向均为－400～400 km。

图6绘制了基线长度分别为d=30 km、d=60 km、d=120 km时的定位精度分布图。从图中可以看出:基线长度越长，定位精度越精准，说明基线长度对定位精度产生了影响。从图中可以看出基线长度对定位精度的影响较大，且定位精度的大小和基线的长度近似呈线性关系。

图6 基线长度d单独作用对定位精度的影响

图7分别为d=30 km、d=60 km、d=120 km时的相对误差曲线图。仿真条件:测向精度σθ=3 mrad;站点位置精度σp=10 m。

图7 基线长度d对相对误差的影响

图7绘制了基线长度对相对误差影响的曲线图。总体来看，当辐射源与两个基站的距离超过25 km后，随着距离的增加，相对误差均呈现增长趋势且基线长度越长，定位精度越精准。当d=30 km时，相对误差小，定位精度在整个作用范围内能达到良好水平;d=60 km、d=120 km时相对误差减小、定位精度稍有提高，在整个作用范围内能达到优秀水平。因此希望在配置允许范围内尽可能加大基线长度。

3 结束语

根据相对误差曲线图可以得出，随着辐射源运动距离的增大，相对误差随之增大，在超过50 km时，相对误差成稳定增长趋势。基线长度越长，定位精度越精准;同样，站点位置精度越低，相对误差也略有增大;但是这两个因素对相对误差的影响并不是关键的，可以忽略不计。测向精度对相对误差产生主要影响，且相对误差大小和测向精度大小近似呈线性关系。由此可知，在运用既定性能观测单站所组成的系统进行定位时，应合理选择基线长度，准确测量各站点坐标及方向角信息，才能提高整个系统的定位精度。

［1］ 赵国庆．雷达对抗原理［M］．西安:西安电子科技大学出版社，1999．

［2］ 许耀伟．一种快速高精度无源定位方法的研究［D］．长沙:国防科学技术大学，1998．

［3］ 刘军，曾文锋，江恒，等．双站测向交叉定位精度分析［J］．火力与指挥控制，2010，35(8)(增刊):12－14．

［4］ 朱永文，娄寿春，韩小斌．双基地雷达测向交叉定位算法的误差模型［J］．现代雷达，2006，28(7):18－20．

［5］ 丁鹭飞，耿富录．雷达原理［M］．3版．西安:西安电子科技大学出版社，2004．

［6］ 孙仲康，郭褔成，冯道旺．单站无源定位跟踪技术［M］．北京:国防工业出版社，2008．