基于DSP的单频激光实时信号解调软硬件研究

王 坚,杨 军

(哈尔滨工程大学 理学院,哈尔滨 150001)

0 引 言

随着精密机械加工工艺的不断发展,对物体实现微小振动和微小位移精确测量的研究逐渐得到了人们广泛的重视。在众多测量方法中,激光干涉测量法由于其测量精度高、设计结构简单、适用于各种复杂环境和动态范围大等优点而得到了广泛的应用。由于激光干涉仪最终的测量信号都是以相互正交的信号形式给出的,所以,正交相位实时解调技术的实现与高精度激光干涉仪测量就显得密不可分了。为了保证正交相位实时解调的实现,不仅需要采用合适的解调算法,例如:非线性误差校正算法和细分查表等,同时,还需要搭建高速数据采集系统和高速数据处理系统为正交相位解调提供高效的硬件平台。

2004年,美国学者 Mark A.Zumberge和Jonathan Berger等人,在其搭建的自由空间型Michelson干涉仪和M-Z光纤干涉仪系统中,以DSP为核心器件实现了对正交信号的实时解调[1]。该正交信号实时解调系统通过12位的AD转换器直接与DSP(Bitt Ware Models BITSI-DAQ and BTCP-4062-3)相连,并且,以100 kHz的采样率对两个正交条纹信号进行采样,并在DSP内构造了截止频率为200 Hz的三阶低通滤器,对数字输入信号进行滤波处理。解调系统的相位分辨率达到了 22 μ rad,电路的噪声最低为 0.5 pm/ Hz-1/2。也是在2004年,美国学者 Taeho Keem和Satoshi Gonda等人基于DSP处理器提出了一种新的干涉仪实时解调方法[2]。该方法中,四路干涉仪正交输出信号经过预放大后由14 Bit精度的ADC完成数模转换,数字信号被直接传输给DSP处理器,经过算法处理后最终由16 Bit精度的DAC完成数据输出工作。该实时解调方法以TI公司的TMS3206071型DSP处理器为核心器件,完成的正交信号的实时解调。此外,为了消除电路噪声,还在DSP内部实现了截止频率为10 Hz的数字低通滤波器,最终使干涉仪标准误差降到了5 μ m的量级。韩国学者Jong-Ahn Kim和Jae Wan Kim等人于2009年基于NI公司的PIC-7831R型数据采集卡提出了一种新的正交信号实时解调方法[3]。该解调方案中,以FPGA为核心器件对解调系统的输入输出信号进行高精度同步控制,采用16 Bit位宽的多通道ADC,采样率为200 kHz,实现了2π相位范围内的1 024细分。

激光干涉信号的解调是实现高精度纳米级激光干涉测量的先决条件之一,现在和将来都将是整个激光干涉信号解调领域的重点课题。尽管如此,同时具备集高速数据采集和高速数据采集能力的干涉信号硬件解调系统仍然没有得到广泛的研究。先进可靠的正交信号解调技术可以使激光干涉仪的测量精度得到大幅度的提高,达到纳米甚至亚纳米级。本文围绕单频激光正交干涉信号输出特性,提出了一种基于DSP和FPGA的新的干涉信号实时硬件解调系统,重点对信号的非线性误差校准和条纹细分算法的实时性优化以及硬件系统设计进行了阐述。

1 解调算法原理

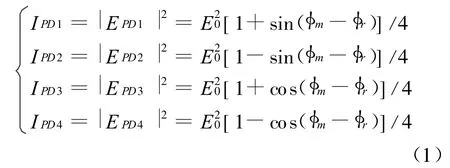
单频激光解调统的输入信号由四路相互正交(相位差各自相差90°)的模拟信号PD1-PD4构成,其表达式见式 (1)[4]。其中,φm-φr为参考光和测量光束间的相位差,记为Δφ,可由参考光束和测量光束之间的光程差2nΔL决定,可表示为:

式中n为折射率;λ为激光器输出波长,本文取632.8 nm;ΔL为参考臂和测量臂之间的臂长差。采用差分的处理方式,则可以得到:

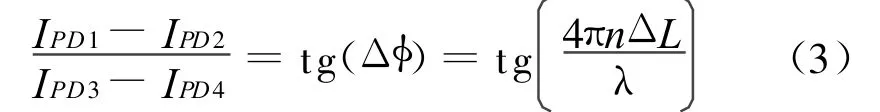
由式 (3)可见,干涉仪的测量结果ΔL体现了待测位移量,实现了对振动的测量。如式(4)所示,四路信号两两相减,便可以得到两路正交的干涉信号:

式中h,k分别为直流分量;a,b为交流幅度大小;Φ为待解调相位;δ为两路信号之间的相位差。理想条件下,h=k=0,a=b=1,δ= π/2或者3π/2。受到元器件的非对称性以及光电探测器的光响应度不同等因素的影响,将使干涉仪输出信号中引入非线性误差,也即h≠k≠0,a≠b≠1,δ≠π/2或3π/2。以Ix为横纵坐标,Iy为纵纵坐标绘制二维图形便可以得到理想情况下和包含非线性误差的单频激光干涉系统输出信号李萨茹曲线,见图1。

本文中,干涉信号解调的重点就是通过采样数据计算并消除式(4)中的非线性误差,最后得到与位移相对应的采样信号相位值。算法设计主要采用的语言为C语言和汇编语言,使用的开发工具为DSP的集成开发环境CCS3.3。软件算法实现的主要功能包括:数据的定浮格式的转换、待解调信号的最小二乘椭圆参数拟合、待解调信号的非线性校正、解调信号的相位计算[6-9]以及解调信号的浮定点格式的转换。

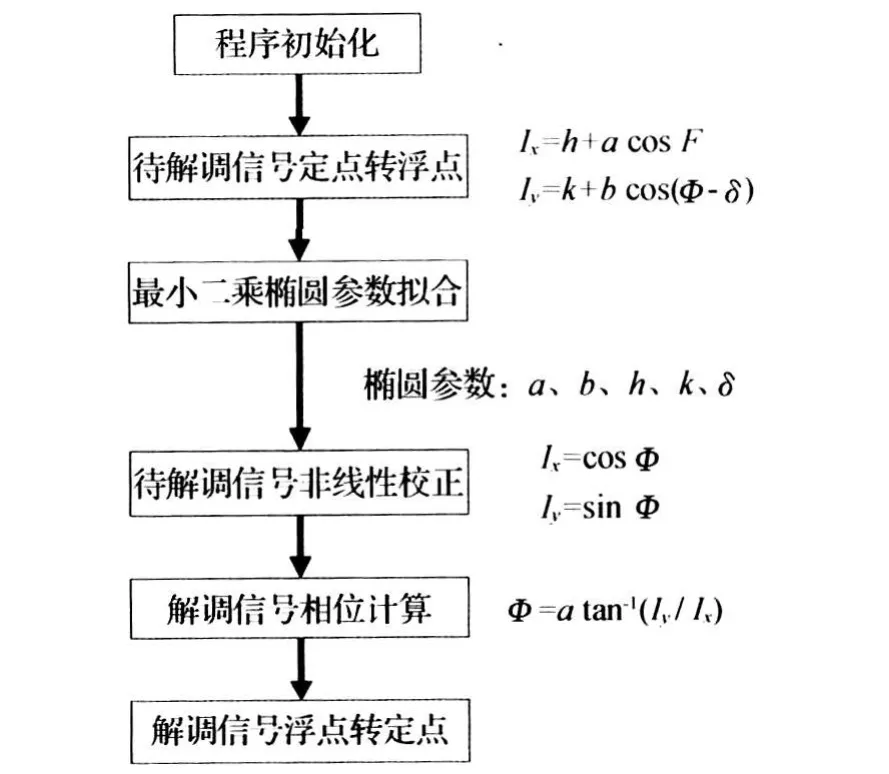
图2 解调算法流程图Fig.2 Flow chart of demodulation

2 算法优化

由于本文中的信号解调系统有时实性的要求,所以,仅仅通过信号解调原理完成算法(图2)的编写,是无法实现快速解调功能的。因此,在实现算法功能的基础上需要对算法性能进行优化,提高算法的效率。算法优化的过程实质上是通过提高硬件资源的并行利用率来提高程序的运行速度,以减少程序运行的周期数和对存储器的访问时间。总的来说,算法的优化手段可以分为算法级别的优化和代码级别的优化。

2.1 算法级别的优化

本文中,在求解非线性误差参数时,需要通过大量的采样点求解式(5)中的矩阵M1和M2中的各个元素[10],求解过程中使用到了大量的循环迭代累加计算,该部分的计算非常耗时。以矩阵M1的各个元素求解为例,若采用每次迭代都完成各个元素的一次累加,并且,单次累加值均由当前采样对计算得到的思想,那么,实现矩阵各个元素的求解就需要512×25次加法,各个元素本身的单次迭代累加值还由采样对的若干次乘法实现,例如,项的单次累加值就需要三次乘法=)。通过观察式 (5)可以发现,矩阵为对称矩阵,矩阵中各个元素以对角线为对称轴对应相等。所以,在循环迭代累加过程中,可以只求解位于M1矩阵对角线上侧的元素值,在完成整个迭代累加过程后,将对角线上侧的元素值直接赋给下侧对应元素即可省略大部分乘加运算,基于该原理M2中的部分元素也可以由M1中元素赋值求得。经过优化后,该部分计算的耗时可以缩短一半。

最小二乘椭圆拟合算法中,还需要对式 (5)中的矩阵M1求解逆矩阵。常见的逆矩阵求解方法有两种,定义求解法和初等行/列变换法。定义法求解逆矩阵需要进行多次的矩阵的秩的求解和矩阵的行交换,要使用大量条件判别和乘加运算。而初等行变换法求解逆矩阵则是利用初等行/列变换实现矩阵(M1|E)到矩阵(E|)的变换,E为单位矩阵,相对于前者,其运算量少,有利于实时解调的实现。在本文中,用初等变化代替定义法求解逆矩阵后,算法效率提高了10倍。

2.2 语法级别的优化

本文中,算法程序的主要代码采用了C语言编写,而C语言是不能被处理器直接识别的,需要通过编译器进行编译转换成机器代码后才能够在处理器中运行。所以,提高编译器的编译效率在程序优化环节中显得非常的重要。在最小二乘椭圆拟合部分中,需要借助大量的矩阵来完成非线性参数a、b、h、k和δ的计算。在代码编写过程中,矩阵的表示则需要借助数组来完成。在进行语法级别的算法优化之前采用的矩阵形式为二维矩阵。由于编译器对一维数组的编译效率高于二维数组,所以,可以将二维矩阵 [M1]5×5计算简化为一维矩阵 [M1]25×1运算,该部分算法优化后,计算耗时性能在之前的优化基础上可以提高30倍。

3 硬件解调系统设计

本文给出的单频激光实时信号解调系统硬件总体架构见图3,由一套基于FPGA的高速信号采集系统和一套基于DSP的高速数据处理系统构成。FPGA采用了Altera公司的EP3C25F324C8芯片,DSP采用了TI公司的浮点型高速芯片TMS320C6713B300。首先,通过前端的模拟硬件电路实现激光干涉仪的光电信号转换和信号调理。经过调理的模拟信号被送入差分ADC进行差分数模转换,并且经由FPGA控制实现数字信号从ADC部分传输到外挂FIFO的数据传输。通过DSP的EDMA可以将外挂FIFO的数据传输到高速数据处理系统的外挂SDRAM中。当DSP完成算法处理后,数据会经由DSP的HPI被传回FPGA。经过处理后的信号可以经过DAC向外输出,同时,也可以经过FPGA外挂的USB芯片传输给上位机。为了保证在ADC不间断采样的情况下,数据传输通路不出现数据堵塞,在FPGA内部开出四片FIFO缓存区域,一片ADC对应两片FIFO,一片FIFO对应于ADC采样数据的存储,另一片则对应于FPGA的数据传输源,当前传输工作完成后,调换两片FIFO的功能即可完成整个高速数据采集系统的ADC不间断采样和FPGA的连续数据传输。在高速数据采集系统和高速数据处理系统之间加入一片外挂FIFO,在DSP处理一片ADC采集数据的同时,另一片ADC的采集数据被存入外挂FIFO中等待处理,该结构使得数据处理系统和数据采集系统相互独立,为解调系统的高速运行提供了保障。实时信号解调系统实物图见图4。

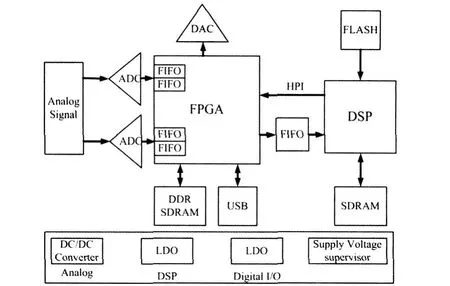
图3 单频激光实时信号解调系统硬件总体架构图Fig.3 Block diagram of demodulation system

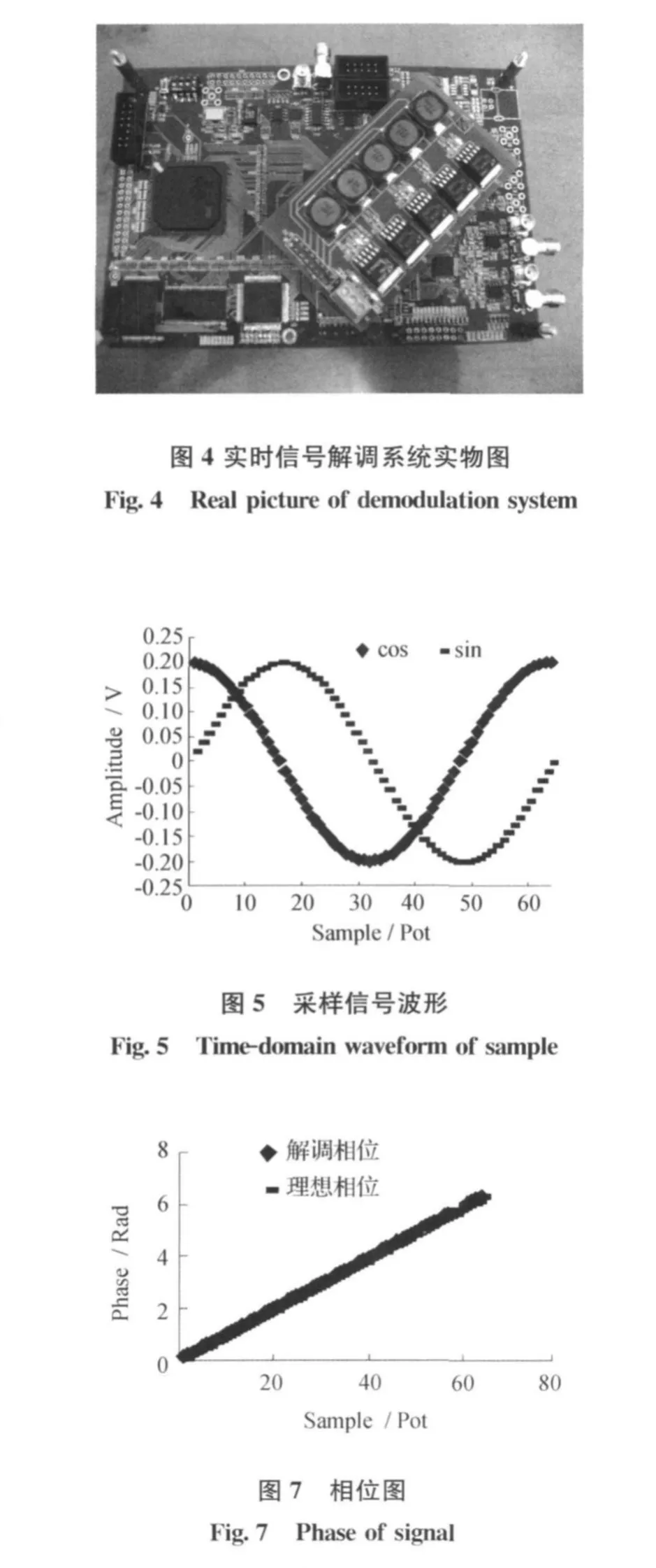
4 试验结果及分析

通过构建的基于DSP和FPGA的干涉信号实时硬件解调系统,对干涉信号进行了实时的高速数据采集与处理,采样率为1 MHz,采样信号和解调信号时域波形见图5、图6。由图5、图6可知,实时解调系统完成了对干涉信号的采样,并实现了对信号的非线性校正,校正后的干涉信号保持了正交特性,且幅值为1。相位解调结果见图7、图8,由图可知,解调相位与标准相位的误差在0.001 5 Rad左右,与理论的2π相位4 096细分查表误差相符。

[1]Mark A.Zumberge,Jonathan Berger,Matthew A. Dzieciuch,et al.Resolving Quadrature Fringes in Real Time[J],Applied Optics,2004,43(4):771-775.

[2]Taeho Keem,SatoshiGonda,Ichiko Misumi,et al.Removing Nonlinearity of a Homodyne Interferometer by Adjusting the Gains of Its Quadrature Detector Systems [J].Applied Optics,2004,43(12):2 443-2 448.

[3]Jong-Ahn Kim,JaeWan Kim,Chu-Shik Kang,et al.A Digital Signal Processing M odule for Real-time Compensation of Nonlinearity in a Homodyne Interferometer Using a Field-programmable Gate Array[J].Measurement Science And Technology,2009,20(1):017 003.1-017 003.5.

[4]段 莉.正交偏振激光干涉振动测量方法与实验研究[D].哈尔滨:哈尔滨工程大学,2008:11-15.

[5]刘彬彬,苑勇贵,王新星,等.偏振激光干涉仪的非线性误差实时校正方法[J].光学学报,2010,30(9): 2 585-2 589.

[6]安新源,周宗潭,胡德文.椭圆拟合的非线性最小二乘方法[J].计算机工程与应用,2009,45(18):188-190.

[7]Chien-ming Wu,Ching-shen Su and Gwo-Sheng Peng. Correction of Nonlinearity in One-frequency Optical Interferometry[J].Measurement Science And Technology,1996,7(1):520-540.

[8]闫 蓓,王 斌,李 媛.基于最小二乘法的椭圆拟合改进算法[J].北京航空航天大学学报,2008,34 (3):295-298.

[9]C.M.Wu,C.S.Su,G.S.Peng,et al.Polarimetric,Nonlinearity-free,Homodyne Interferometer for Vibration M easurement[J].Metrologia,1996,33 (1):533-537.

[10]王新星.正交偏振激光测量的信号解调方法研究[D].哈尔滨:哈尔滨工程大学,2008:17-18.