粘弹性圆柱体运动微分方程的建立

张波

(陕西理工学院土建系,陕西汉中723001)

我们实际生活中遇到的很多材料常同时具有弹性和粘性两种不同机理的形变,如塑料、橡胶、混凝土和岩石等材料,然而从粘弹性材料这个角度出发来研究问题的人较少[1-2]。本文在前人研究成果的基础之上,将轴向流动中的圆柱体视为粘弹性材料,并取微单元进行受力分析,运用D' Alembert原理建立其运动微分方程,并引入Kelvin模型的微分算子,得到了轴向流动中Kelvin模型粘弹性圆柱体的运动微分方程。

1 粘弹性圆柱体的运动方程

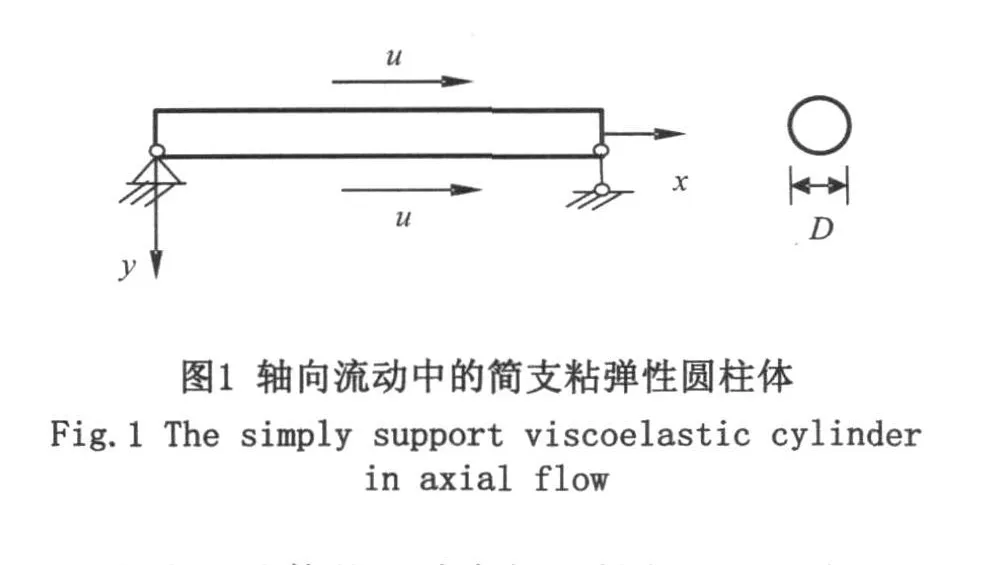
轴向流动中两端简支的粘弹性圆柱体如图1所示。设y为圆柱体挠度,m为圆柱体单位长度质量,ma为圆柱体单位长度附加质量(ma= ρ VCm,其中,ρ为流体密度,V是圆柱体的体积,Cm为附加质量系数),u为沿圆柱体轴向的流动速度,EI为抗弯刚度,l为圆柱体长度,D为圆柱体直径。

对于单位长度上的阻力FN和FL有

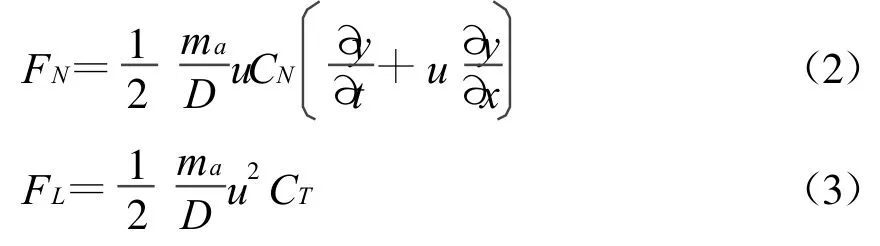
拉力T可以表示为

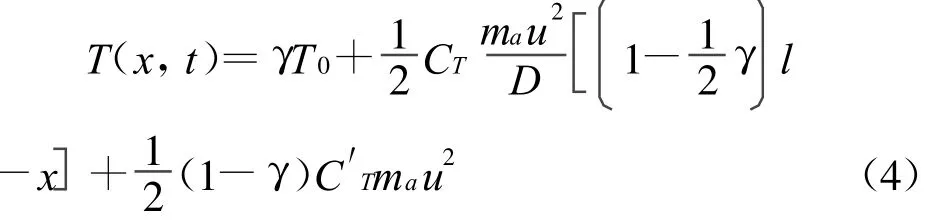
粘性阻尼影响力FD可以表示为

式中 CT—圆柱体纵向阻力系数;CN—圆柱体横向阻力系数;Cv—有效粘性阻力系数;γ—常数(圆柱体下游受支承时 γ=1,下游端自由或弹性支承时γ=0),C′T—自由端的形状阻力系数;T0—初始轴向拉力。

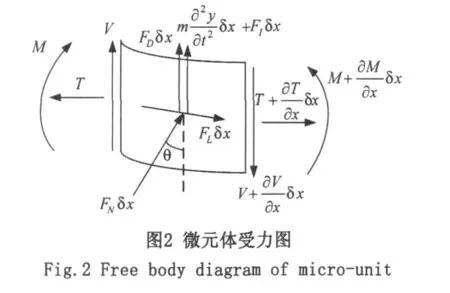
根据达朗伯原理[4],对微元分别列出x、y方向力的平衡方程,并考虑到当 θ→0时,有sinθ≈0,cosθ≈1,则有

如果忽略转动惯量,则x-y平面上的转动平衡方程为

对于粘弹性材料,应力和应变之间的关系为

式中P、Q—微分算子。

弯矩M(x,t)和挠度y(x,t)有如下的微分关系

根据式(6)、式(7)、式(8)、式(9)、式(10),得到粘弹性圆柱体在横向流动中的运动微分方程

把式(1)、式(2)、式(3)、式(4)、式(5)代入式(11)可以得到粘弹性圆柱体的运动微分方程

2 Kelvin模型的运动微分方程

假定圆柱体的材料服从Kelvin模型[5],则有

式中σ—正应力;e—线应变;E—弹性模量;η—粘性系数。

将式(14)代入式(12),并略去二阶小量,即可得到Kelvin模型粘弹性圆柱体在轴向流动中的运动微分方程

引入下列无量纲量

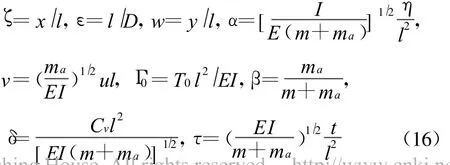
将方程(15)化为无量纲方程

式中β—质量比;τ—无量纲时间;v—无量纲流动速度;α—无量纲延滞时间。

3 结束语

运用D'Alembert原理,引入Kelvin模型的微分算子,得到了轴向流动中Kelvin模型粘弹性圆柱体的运动微分方程,最后再引入无量纲量将Kelvin模型粘弹性圆柱体的微分方程化为无量纲方程,为轴向流动中粘弹性圆柱体的动力特性分析奠定了基础。

[1]GRIFFIN O M,SKOP R A,KOOPMANN G H.The vortex -excited resonant vibrations of circular cylinder[J].Journal of Sound and Vibration,1973(31)：235-249.

[2]ZHOU C Y,SO R M C,LAM K.Vortex-induced vibration of an elastic circular cylinder[J].Journal of Fluids and Structure,1999(13)：165-189.

[3]CHEN S S(美),圆柱结构的流体诱发振动[M].冯振宇,张希农,译.北京：石油工业出版社,1988.

[4]倪振华.振动力学[M].西安：西安交通大学出版社, 1989.

[5]杨挺青.粘弹性力学[M].武汉：华中理工大学出版社, 1990.