基于层次故障树的地面电源诊断优化方法研究

吴玉彬，张合新，吕永佳

（第二炮兵工程学院301教研室，陕西 西安 710025）

测试与诊断的快速性、准确性、完备性是决定和影响导弹部队快速反应能力和生存能力的重要问题。为了适应未来复杂的战场环境，满足越来越先进、精确的现代化导弹装备的需求，需要对导弹武器各系统的测试和诊断方式进行改进。随着导弹地面电源系统性能的提高及其结构的复杂化，其故障发生的机率大大提高，各故障相关的因素也多种多样，以至于操作号手感觉难以掌握繁杂的关于故障的知识[1]。现行的导弹地面电源系统故障诊断的一般手段是：操作号手根据获得的故障现象，利用自己的经验或者查阅故障手册进行故障诊断。根据人工记忆或经验的诊断方式效率较低，已不能满足战时快速诊断及操作的需要。另一方面对于复杂系统的故障诊断而言，如何提高其测试与诊断的效率也是急需解决的重要问题。其目标是在测试与诊断的过程中，能够综合各类因素、采用系统分析的方法，将相对重要性大的故障因素优先测试而将相对重要性弱的因素最后测试，从而大大减少故障诊断的复杂程度，提高故障源搜寻时的一次命中率，避免诊断测试的盲目性，进而省去大量的测试过程，达到优化故障诊断策略的目的[2-3]。

综合考虑导弹地面电源系统故障诊断的实际需求，结合故障树及层次化分析法 （Analytie Hierarchy Proeess，AHP）的有关特性，以30 KVA中频逆变电源为例，首先对故障现象进行故障树建模，并在此基础上提出了基于层次化故障树分析法的30 kVA中频逆变电源故障诊断策略优化技术，进行了理论的分析及实际验证。

1 故障树及层次化分析方法

1.1 基本理论

故障树分析（Fault Tree Analysis，FTA）的原理是一种将系统故障形成原因按树枝状逐级细化的图形演绎方法，可用于大系统可靠性、安全性分析和风险评价[4]。它通过对可能造成系统故障的各种因素（包括硬件、软件、环境、人为因素等）进行分析，画出逻辑框图（即故障树），再对系统中发生的故障事件，作出总体至部分、按树枝状逐级细化的分析，并在方案与初步设计阶段对系统进行可靠性、安全性分析，常用于系统的故障分析、预测与诊断[5]。

对于简单的系统，应用传统故障树分析法对系统进行逐级排查就可以快速实现故障的分析与定位，并且借助重要度的概念，对导致顶事件发生的最小割集进行评测，确定其重要程度[6]。然而当系统结构和功能十分复杂时，传统的分析既费时又费力，效率很低，无法实现故障快速定位。层次化分析方法的思想基础与系统分析的原则是一致的[7]。在对事物进行决策分析时，能对定性问题和定量问题进行综合分析处理，并得到明确的定量化结论，以优劣排序的形式表现出来，对事物的评判决策过程十分简便。丰富的数学原理以及能够汲取决策者个人或集团的阅历、经验、智慧、判断能力，从而使得诊断策略建立在更扎实的理论基础上。

层次化分析方法是将决策问题的有关元素分解成目标、准则、方案等层次，在此基础上进行定性分析和定量分析的一种决策方法。该方法的特点是在对复杂决策问题的本质、影响因素及其内在关系等进行深入分析后，构建一个清晰的层次结构模型，然后引入测度理论，通过两两比较，用相对标度将人的判断标准用量化的形式表示出来，而后逐层建立判断矩阵，在此基础上逐个求解各个判断矩阵的权重，最后计算方案的综合权重并进行层次总排序，按照各个方案权重的大小选择合适的方案[8]。

1.2 层次化分析的步骤

层次分析法本质上是一种决策思维方式，它具有人的思维分析、判断和综合的特征。它的基本思路可以分为以下6个步骤[9]。

第一步，将复杂的问题层次化。决策者根据问题的性质和要达到的目标，首先制定出目标层，目标层通常为一个元素，是问题的最终目的。把影响问题决策的因素分为几大类作为目标层下面的准则层。指标层是准则层的细化，其中的元素均隶属于准则层中的一个或多个元素。最后一层为决策方案层，列出待选的各种方案。这样，就把问题按照各因素之间的隶属关系和相互关联度分层，形成自上而下的逐层支配的关系，也即形成一个递阶层次结构，如图1所示。

图1 递阶层次结构Fig．1 Pass class time structure

第二步，采用标度法[10]形成判断矩阵。层次分析法的信息基础就是判断矩阵。假设有m个指标Z1，Z2，…，Zm，给定一个准则，利用某一标度法对指标Zi和Zj作相互比较判断，即可获得相对重要度的数据aij。以此类推，可构建一个m阶的矩阵：

矩阵A就是判断矩阵。判断矩阵的实质是一个主观评判的过程，通过专家对某一层次中所有元素，以所属的上一层次中某元素为准则进行两两比较，确定哪一个重要和重要的程度。判断矩阵有如下的特性：

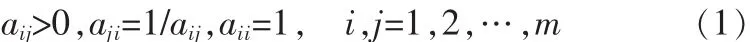
第三步，检验判断矩阵的一致性[11]。进行一致性检验可通过计算一致性比例CR来决定，

表1 传统AHP法比例标度Tab.1 Traditionalm ethod proportion scale for AHP

其中：

称为一致性指标。RI称为平均随机一致性指标；λmax为特征方程的最大特征根；n为比较判断矩阵A的阶数 （也是该层次所含的因素个数）。RI的取值规则如表2所示。

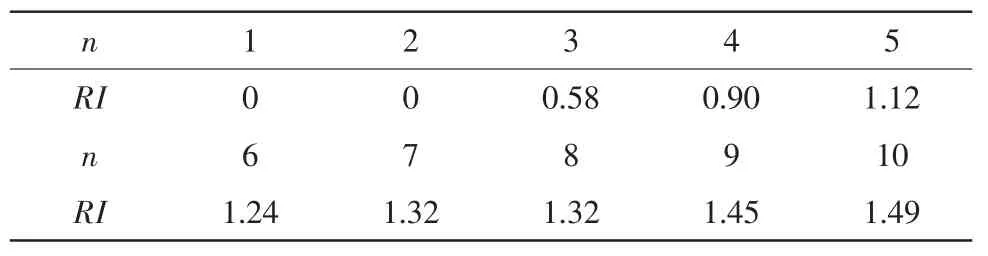
表2 RI取值规则Tab.2 RIvalues rules

若CR≤0．1，则认为该层次单排序的结果有满意的一致性，否则需要调整A的元素取值。

第四步，层次总排序。计算同一层次中所有元素对于最高层总目标的相对重要性标度称为层次总排序。这一过程是从最高层次向最低层次逐层进行的。设已计算出k-1层相对于总目标的排序权重向量为：

式中m为k-1层次所含的因素个数。而以第k-1层第j个因素作为比较准则时，第k层各因素相对重要性标度为：

式中n为k层次所含的因素个数。bkj（i）为第k层第i个因素的相对重要性标度。令 Bk=（bk1，bk2，…，bkm），则第 k 层各因素相对于总目标的排序权向量ak由（6）式给出：

一般的，有排序权重公式：

式中a2为第二层因素的排序权重向量；h为层次数。

第五步，层次总排序的一致性检验。考虑到人们在对各层元素作比较时，尽管每一层次中所用的比较尺度可能基本一致，但各层之间仍可能有所差异，而这种差异将随着层次总排序的逐层计算而累计起来，为此需从评价模型的总体上检验一下这种差异程度的累积是否显著，上述检验过程称为层次总排序的一致性检验。这一工作也是从高到低逐层进行的。设已得到以k-1层第j个因素为比较准则时，第k层各因素两两比较的层次单排序一致性指标为CIk-1j，平均随即一致性指标为RIk-1j，则第k层次的一致性检验指标有：

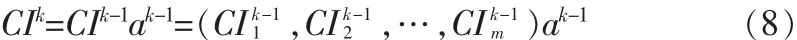
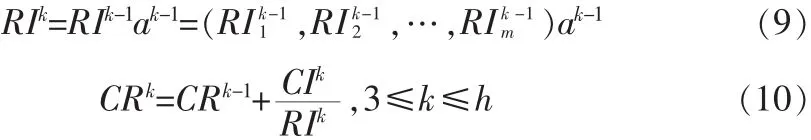
当CRk≤0．1时，可认为评价模型在第k层水平上整个判断达到了局部满意一致性。若上述检验过程一直完成到第h层次（最低层次），并有 CRh≤0．1，则可认为该评价模型在作逐层比较时，对所有层次和所有因素作比较所用的尺度达到了总体上的满意一致性，因而所得到的层次总排序权重向量W=ah是可信的，可以用来做排序和优选之用。

第六步，通过逐层计算，得到方案层对目标层的权重，比重最大的一个为待选方案中的最优方案。

2 故障树建模

将层次故障树诊断方法引入导弹地面电源系统故障诊断中，首先必须对该电源系统进行分析，并对各故障状态进行故障树建模。故障树建造过程的实质是寻找出所研究的系统故障和导致系统故障的诸因素之间的逻辑关系，并将这种关系用故障树的图像符号（事件符号与逻辑门符号）表示，成为以顶事件为根，若干个二次事件和基本事件（底事件）为干枝和分枝的倒树图形。下面以故障现象“逆变电路能启动，但输出的490 Hz频率不正常或不稳定。”为例进行故障树建模分析。

故障现象：逆变电路能启动，但输出的490 Hz频率不正常或不稳定。

该故障现象，根据导弹地面电源系统工作原理及系统层次模型，可以推断出故障发生在逆变分系统和整流分系统。故障部件可能为RC调频器件、逆变触发电路，分析至此，将故障范围缩小到部件级。

对部件级故障进行故障树分析：假如故障发生在RC调频器件，则故障原因为“时钟振荡”电路IC7（74132）故障，或者直流分压电阻R8～Rl0有烧坏的，或者滤波电容有漏电或开路的，从而引起输出的490 Hz频率不稳定；假如故障发生在逆变触发电路，则可能原因是分配缓冲电路IC2（7416）、选通电路 IC5/6（7416）、脉冲放大电路 T6～T11及其相关外围器件故障，另外逆变可控硅性能变坏时，也会导致此现象。单元模块故障树如图2所示。

图2 单元模块故障树Fig．2 Unitmodule fault tree

3 层次故障树分析

层次故障树分析的基本思路是：首先将故障诊断树转化为符合层次化分析方法的递阶层次结构；其次对变换后的递阶层次结构进行层次化分析，求得各底事件或割集的相对测度值，将相对重要性大的故障因素优先测试而将相对重要性弱的元素最后测试，从而可以大大减少故障诊断的复杂程度，同时也必然使故障源搜寻时的一次命中率大大提高，避免诊断测试的盲目性，省去大量的测试过程，达到优化故障诊断策略。

以故障“逆变电路能启动，但输出的490 Hz频率不正常或不稳定”为例，对基于层次故障树的诊断优化方法进行验证。首先将图2所示故障树转化为递阶层次结构。

在将故障树结构向递阶层次结构转换的过程中，首要解决的就是故障树中逻辑符号的处理。文献1提出两种解决的方法，即直接转化法和间接转化法。为了能够清楚地说明上述转换过程，以图2所示的故障树为例进行说明。

STEP1将故障树的顶事件“逆变电路能启动，但输出的490 Hz频率不正常或不稳定”列为A级元素。

STEP2进行B级遍历，并分级编号，得B级元素如表3所示。

表3 B级元素Tab.3 B level element

STEP3进行C级遍历，并分级编号，得C级元素如表4所示。

表4 C级元素Tab.4 C level element

由此获得的递阶结构图如图3所示。

图3 图2的递阶层次结构Fig．3 Pass class time structure for Fig．2

判断矩阵

C层对于目标层A的一致性检验：

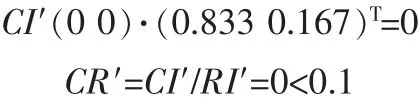
满足整体一致性要求。C层次对于A的总排序可用表5所示。

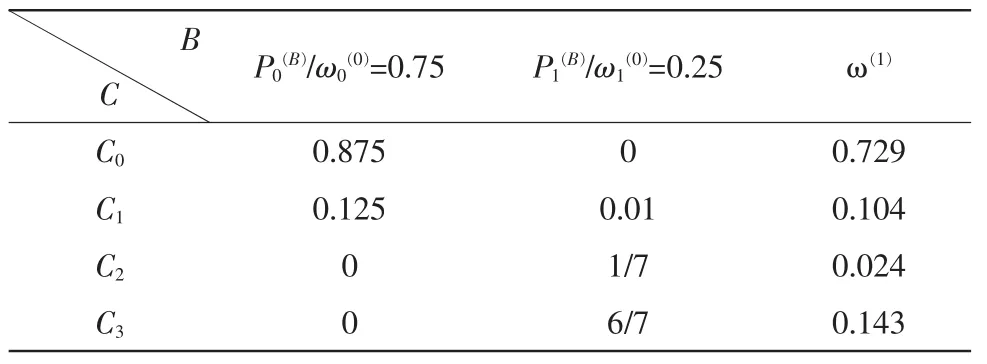
表5 C层次对于A的总排序Tab.5 C level total order for A

由此可以看出，C3（逆变可控硅损坏，导致逆变触发电路故障），C2（逆变单元可控硅的触发脉冲Ⅲ～Ⅱ6异常，导致逆变触发电路故障），C0（直流分压电阻 R8～Rl0烧坏，导致整流主电路故障），C1（滤波电容漏电或开路，导致整流主电路故障）这4个故障因素对于总目标的相对重要性排序为 C0＞C3＞C1＞C2。在故障诊断策略制定的过程中，按照上述顺序，将相对重要性大的故障因素优先测试而将相对重要性弱的元素最后测试，达到优化故障诊断策略。

4 结束语

从导弹地面电源系统故障诊断的实际需求出发，首先采用故障树的方法构建了典型故障及其故障原因之间的故障树模型，其次针对传统故障树模型中，重要度评价方法存在的问题，引入层次化分析的方法，实现故障因素对于总目标的相对重要性的量化评价和排序，进而可实现诊断策略的优化。理论分析以及实验验证说明，故障树模型能够快速地实现导弹地面电源系统故障的分析和定位，层次化分析方法比重要度评测方法更为高效和实用。

[1]黎清海，朱新华．基于层次分析的火控系统故障诊断专家系统[J]．电光与控制，2006，13（4）：64-68．

LIQing-hai， ZHU Xin-hua．Fault diagnosis expert system for fire control system based on hierarchy analysis[J]．Electronics Optics ＆ Control， 2006，13（4）：64-68．

[2]许斌，周鸣歧．测试点优化及故障诊断树生成技术[J]．国外电子测量技术，2006，25（3）：15-19．

XU-bin， ZHOU Ming-qi．Optimal test point selection and diagnosis tree generation technique[J]．Foreign Electronic Measurement Technology，2006，25（3）：15-19．

[3]朱大齐，于盛林．基于知识的故障诊断方法综述[J]．安徽工业大学学报，2002，7（2）：15-18．

ZHU Da-qi， YU Sheng-lin．Survey of knowledge-based fault diagnosis methods[J]．Journal of Anhui University of Technology：Natural Science，2002，7（2）：15-18．

[4]Hauptmanns U．A decision-making framework for protecting process plants from flooding based on fault tree analysis[J]．Reliability Engineering and System Safety．2010，95（9）：970-980．

[5]苏晓勤．故障树分析算法改进研究与实现[D]．河北：河北工业大学，2002．

[6]韦振中．各种标度系统的随机一致性指标[J]．广西师范学院学报，2002，45（21）：26-29．

WEI Zhen-zhong．Random index of various kinds of scale system[J]．Journal of Guangxi Teachers Education University：Natural Science Edition，2002，45（21）：26-29．

[7]宋剑．模糊层次分析法在国际航运投资决策中的应用研究[D]．大连：大连海事大学，2008．

[8]许化东．基于故障树分析方法的汽车故障诊断专家系统的研究[D]．合肥：合肥工业大学，2002．

[9]FerdousR，Khan FI，Veitch B，etal．Methodology for Computer-Aided FaultTree Analysis[J]．ProcessSafety and Environmental Protection，2007，85（1）：70-80．

[10]蔡海鸥，张若欣．AHP一致性的概率检验法[J]．数学的实践与认识，2010（7）：154-160．

CAIHai-ou，ZHANGRuo-xin．Testing Consistency of Judgment Matrices in AHP with Method[J]．Mathematics in Practice and Theory，2010（7）：154-160．

[11]何堃．层次分析法的标度研究[J]．系统工程理论与实践，1997，17（6）：58-61．

HEkun．A study on the scale of analytic hierarchy process[J]．Systems Engineering-theory ＆ Practice，1997，17（6）：58-61．