基于主-从模式的正面吊垂直升降协调控制方法
刘 宜,方 静,钱 玮,李传宝,张 丽,许 涛
(1中国科学院 合肥智能机械研究所,安徽 合肥 230031;2安徽合力股份有限公司 重装事业部,安徽 合肥 230022;3.合肥工业大学 计算机与信息学院,安徽 合肥 230009)
在集装箱正面吊运机(简称正面吊)的搬运、堆垛作业中,驾驶员经常需要同时协调大臂的俯仰与伸缩动作,使吊具在俯仰和伸缩2个油缸的轴线所确定的平面内做垂直方向的运动,以便将集装箱垂直上升或下降到预定高度.由于正面吊的俯仰和伸缩2个油缸共用同1个主油路,且2个油缸的负载存在显著的差异,从而在相同的比例阀开度下进入油缸的流量差别较大,并且2个油缸的流量需要非线性的变化才能满足垂直升降的要求,造成单独依靠驾驶员的人工协调控制难以实现精确的垂直升降运动,降低了操作的可靠性与准确性,并增加了驾驶员的工作强度.因此,研究开发高性能的垂直升降控制技术,成为提高正面吊性能水平的一项关键技术.
正面吊的垂直升降控制实质是对俯仰、伸缩2个油缸的运动进行协调控制以实现吊具的垂直升降运动.对于多个运动轴之间的协调控制,从各轴相互关系来说可以分为主从模式[1,2]与等态模式[3-6].在各轴动力学特性比较接近的情况下,采用等态模式引入耦合因素对各轴的运动进行协调控制,可以取得较好的运动效果.而在各轴动力学特性相差比较大的情况下,由动态响应快的运动轴跟随动态响应慢的运动轴,便于实现各轴之间的协调运动.
本文针对正面吊垂直升降的控制问题,通过建立正面吊吊具运动模型,分析了垂直升降时大臂与变幅臂的伸出长度曲线与速度曲线,结合正面吊液压系统的基本组成,提出了基于主-从模式的协调控制方法,以变幅缸运动为主运动,伸缩缸运动为从运动,对变幅缸比例阀开度按照参考开度曲线进行开环控制,而对变幅缸比例阀开度按照吊具半径误差采用PID方法进行闭环调节,并通过在合力RS4532型正面吊上的实际实验,验证了本方法的有效性.
1 问题描述
1.1 正面吊液压系统基本组成
正面吊液压系统基本组成如图1所示,该液压系统为开式系统回路,主油泵采用2个105ml·r-1的柱塞泵,由柴油发动机驱动,其中柱塞泵1经组合阀后向制动(行车、驻车制动)与转向系统供油,并经主阀与柱塞泵2合流后给臂架动作、吊具动作供油,柱塞泵2经主阀后为臂架的变幅、伸缩动作与吊具动作供油.主阀用于控制主液压系统,采用负载传感控制,可根据工况的变化自行调节主油泵的输出流量.驾驶员通过操作手柄控制各个比例阀的开度,来操纵臂架的伸缩、变幅以及吊具的伸缩、回转等动作.
由于主阀采用的是阀前压力补偿,在执行俯仰与伸缩的联合动作时,会导致向轻载去的流量多,而向重载去的流量少,需要控制系统对阀的开口量进行控制与补偿.

图1 正面吊液压系统基本组成示意图Fig.1 Schematic diagram of basic components of reachstacker hydraulic system
1.2 正面吊吊具运动简化模型
如图2所示为正面吊吊具运动简化模型,取大臂后支点作为坐标原点,大臂、变幅臂均用其中心线来近似表示,E为大臂中心线与吊具中心线的交点,用来近似表征吊具的运动.吊具的运动由大臂的伸缩运动与变幅臂的变幅运动合成,其中大臂的伸缩运动通过伸缩液压缸实现,变幅臂的变幅运动由变幅液压缸实现.吊具的位置E由大臂的长度lA,大臂与水平面的夹角α唯一确定:

式中:xE为吊具半径,yE为吊具高度.
大臂的长度lA由大臂的固定长度lAO,伸缩液压缸的伸出长度ΔLA确定:

大臂与水平面的夹角α可以根据下式计算:
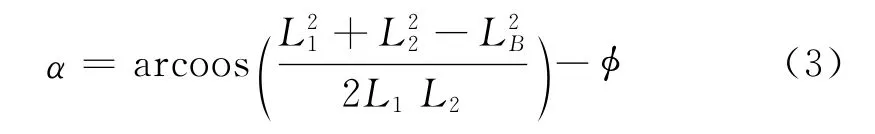
式中:L1为大臂支点O到变幅臂上铰点A的距离;L2为大臂支点O到变幅臂下铰点B的距离;LB为变幅臂上铰点A到变幅臂下铰点B的距离,即变幅臂的长度由变幅臂的固定长度LBO与变幅液压缸的伸出长度ΔLB确定,LB=LB0+ΔLB;φ为OB与水平面的夹角,为一固定的值.

图2 正面吊吊具运动简化模型Fig.2 Simplified kinematic model of reachstacker hanger
综上可见,吊具的位置与伸缩液压缸的伸出长度ΔLA为线性关系,而与变幅液压缸的伸出长度ΔLB为非线性关系,这为协调伸缩液压缸与变幅液压缸的运动增加了难度.
1.3 垂直升降时大臂与变幅臂的伸出长度及速度
为分析在垂直升降时变幅缸与伸缩缸的伸出长度的变化情况,取吊具x轴坐标保持不变的情况下,根据式(1)—(3)计算ΔLA与ΔLB,即不考虑液压缸动态响应的情况,完全从几何的角度进行计算.
在取xE=7m,大臂倾角α从0~55°均匀变化时,计算对应的吊具高度、大臂伸出长度、变幅臂伸出长度.为便于比较大臂伸出长度与变幅臂伸出长度的变化相对快慢,考虑在吊具匀速垂直上升时(即单位时间内吊具高度的变化量恒定),计算大臂伸出长度与变幅臂伸出速度曲线.由于上述数据是一一对应的关系,故取吊具高度为横坐标,绘制相关的曲线,如图3—6所示.

图3 大臂伸出长度曲线Fig.3 Main boom extended length curve

图4 大臂伸出长度的速度曲线Fig.4 Variation curve of main boom extended length

图5 变幅臂伸出长度曲线Fig.5 Luffing boom extended length curve
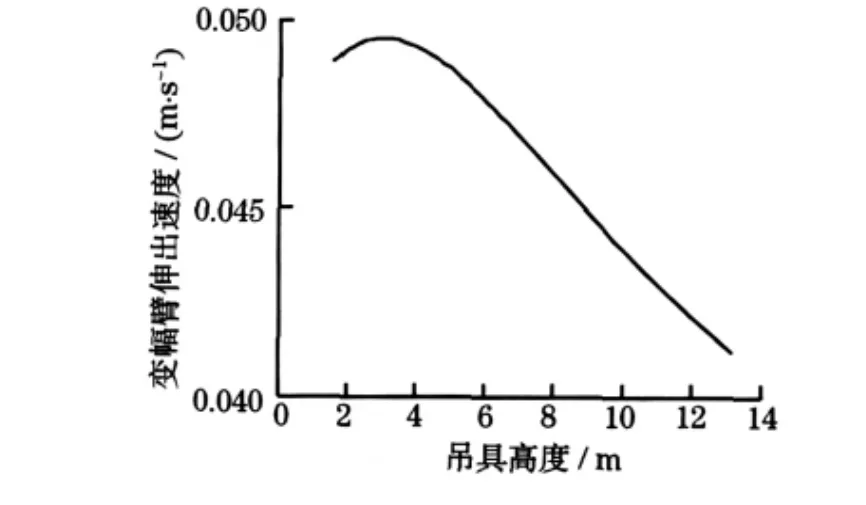
图6 变幅臂伸出长度的速度曲线Fig.6 Variation curve of luffing boom extended length
由图3可见,随着吊具高度增加,大臂伸出长度逐步增大,由图4可见,在吊具匀速垂直上升时,随着吊具高度的增加,大臂伸出的速度是逐步增大的.由图5可见,随着吊具高度的增加,变幅臂伸出长度也是逐步增大,但由图6可见,在吊具匀速垂直上升时,随着吊具高度的增加,变幅臂伸出的速度首先是略微增大,然后是逐步下降.类似地,对于垂直下降的情况,大臂的伸出速度与变幅臂的伸出速度的变化情况是与垂直上升时相反的.由此可见,在吊具垂直升降过程中,若要保持吊具在垂直方向上的匀速运动,需要大臂伸出速度与变幅臂长度伸出速度随吊具高度进行非线性的变化.
2 算法设计
2.1 原理
根据前面的分析,若在垂直升降时期望吊具保持恒定的速度,在吊具高度较小时需要提供变幅液压缸较大的流量,而伸缩液压缸只需要较小的流量,随着吊具高度的上升,变幅液压缸的流量需要逐步减小,伸缩液压缸的流量要逐步增加.
考虑到在垂直升降时,变幅液压缸承担着主要的负载,而伸缩液压缸承担较小的负载,在相同的输入功率情况下,伸缩液压缸的响应速度比变幅液压缸的响应速度要快,因此采用以变幅液压缸为主,伸缩液压缸为从的主从模式进行协调控制,对变幅液压缸的开度按照参考开度曲线进行开环控制,同时根据吊具半径误差对伸缩液压缸的开度进行实时调节以跟踪变幅液压缸的运动.
2.2 变幅缸比例阀开度参考开度曲线的设定
根据1.3节的分析,为使在垂直升降过程中吊具保持恒定的的速度,变幅液压缸的流量需要随吊具高度增加而逐步减小,即其比例阀开度需要随吊具高度增加而逐步减小.为简化计算,并且便于适用于各种情况,考虑到大臂倾角是可以通过传感器直接获取的变量,因此采用变幅缸比例阀开度根据大臂倾角的增大而线性减小,通过多次实验确定:在大臂倾角为0°时开度最大为100%,在大臂倾角为60°时开度最小为20%,对于中间角度,采用线性插值的方法计算对应的开度.
2.3 基于半径误差反馈的伸缩缸比例阀开度闭环控制
在垂直升降时,由于变幅液压缸与伸缩液压缸均在同时运动,若要精确地计算变幅缸伸出长度与伸缩缸伸出长度对半径误差的影响,过程比较复杂,这里采用简单的定性判断方法,根据式(1)—(2)可知,若实际半径大于期望半径,则需要降低伸缩缸的伸出速度,即减小伸缩缸比例阀开度,反之则增大伸缩缸比例阀开度.根据上述原则,以半径误差作为反馈,采用PID控制方法,对伸缩缸比例阀开度进行实时调节.

式中:ui为当前伸缩缸比例阀开度;kP为比例增益;kD为微分增益;kI为积分增益;ei,ei-1分别为当前采样时刻、上一次采样时刻的半径误差;∑ej为当前时刻与过去时刻的所有半径误差累加和.
2.4 算法步骤
(1)获取传感器测量的大臂长度与大臂倾角,计算当前的吊具高度与半径.
(2)根据当前大臂倾角与变幅缸比例阀开度参考开度曲线,采用线性插值计算当前变幅缸比例阀开度.
(3)根据期望半径与实际半径,采用PID方法计算伸缩缸比例阀开度.
(4)当半径误差大于允许的最大值时,设定变幅缸比例阀开度为0;在半径误差小于允许的最小值时,设定伸缩缸比例阀开度为0.
在主控制器中,上述算法按照100ms的周期执行.
3 实验验证
3.1 实验平台
实验平台为合力RS4532型正面吊,车质量为73t,最大载质量为45t,如图7所示,实验所用的吊箱是质量为20t的框架箱.电气控制系统由主控制器、显示屏、集成操作手柄、长角传感器、压力传感器组成,通过CAN总线联成1个完整的集成控制系统,由主控制器来实施车辆统一、协调的控制.主控制器采用德国Hesmor HC-G19型控制器,控制软件采用CoDeSys2.3平台开发编写.
3.2 实验结果
在实验时,发动机转速保持在2100r·min-1,采用吊上质量为20t的框架箱进行试验,通过多次调节,确定PID控制的参数为kP=4.8,kI=0.02,kD=0.01.

图7 合力RS-4532型正面吊Fig.7 Heli RS-4532type reachstack
应用本文提出的主从模式协调控制方法后,在正面吊吊起20t的集装箱时,从半径为7.16m、高度为1.92m处垂直上升到高度13.31m,耗时为21.5s,由图8可见,运动过程中的最大半径误差为0.2m,终点半径误差为0.01m,由图9可见,吊具高度随时间基本呈线性增长,即基本保持在匀速上升的状态,取得了良好的控制效果.在垂直下降时,耗时为33.8s,最大半径误差为0.15m,终点半径误差为0.07m.
与之进行对比的是合力正面吊是原先从国外进口的一款正面吊控制器,在垂直上升时,最大半径误差为1.0m,终点半径误差为1.0m;在垂直下降时,最大半径误差为1.2m,终点半径误差为1.2m,其精度远低于本文提出的主从模式协调控制方法.

图8 垂直上升时吊具半径误差曲线Fig.8 Curve of hanger radius error in vertical lifting

图9 垂直上升时吊具高度曲线Fig.9 Curve of hanger height in vertical lifting
4 结论
垂直升降是提高正面吊工作效率与性能的1项关键技术,需要正面吊控制系统进行实时控制与补偿.本文针对这一问题,通过建立正面吊吊具运动模型,分析了垂直升降时大臂与变幅臂的伸出长度曲线与速度曲线,结合正面吊液压系统的基本组成,提出了基于主-从模式的协调控制方法,以变幅缸运动为主运动,伸缩缸运动为从运动,对变幅缸比例阀开度按照参考开度曲线进行开环控制,而对变幅缸比例阀开度按照吊具半径误差采用PID方法进行闭环调节,通过在合力RS4532型正面吊上的实际实验,验证了本方法的有效性,对于提高国产正面吊的性能水平具有较高的参考价值.
[1]胡国良.盾构推进液压系统同步协调控制仿真分析 [J].机床与液压,2007,35(4):142-144.HU Guoliang.Simulation analyses of synchronization control for shield thrust hydraulic system [J].Machine Tool & Hydraulics,2007,35(4):142-144.
[2]张轲,金鑫,涂宝新,等.250t船尾液压工作平台升降的同步控制方法 [J].船舶工程,2008,30(3):37-40.ZHANG Ke,JIN Xin,TU Baoxin,et al.Synchronization control method for 250thydraulic work platform for assembling rudder and propeller[J].Ship Engineering,2008,30(3):37-40.
[3]SUN H,CHIU G.Motion synchronization for dual-cylinder electrohydraulic lift systems[J].IEEE/ASME Transactions on Mechatronics,2002,7(2):171-181.
[4]SUN D.Position synchronization of multiple motion axes with adaptive coupling control[J].Automatica,2003,39(6):997-1005.
[5]SHANG W,CONG S,ZHANG Y,et al.Active joint synchronization control for a 2-DOF redundantly actuated parallel manipulator[J].IEEE Transactions on Control Systems Technology,2009,17(2):416-423.
[6]SUN D,SHAO X.A model-free cross-coupled control for position synchronization of multi-axis motions:theory and experiments[J].IEEE Transactions on Control Systems Technology,2007,15(2):306-314.

