均匀各向同性湍流的脱体涡数值模拟
吴晶峰 宁方飞
(北京航空航天大学 能源与动力工程学院,北京 100191)
均匀各向同性湍流的脱体涡数值模拟
吴晶峰 宁方飞
(北京航空航天大学 能源与动力工程学院,北京 100191)
采用脱体涡模拟方法对均匀各向同性湍流进行了数值模拟,并与Comte-Bellot实验测量结果进行了对比,验证了该文的脱体涡模拟方法对均匀各向同性湍流模拟的可靠性.初始速度场的生成采用Rogallo所提出的构造方法,初始湍能谱满足Von Karman波谱分布;在对流输运项的选择方面,分别采用二阶中心型格式、四阶偏斜对称型中心格式和迎风型低耗散通量分裂格式,考察它们在均匀各向同性湍流模拟中的计算精度和适用性.同时,通过改变计算域大小以及脱体涡模拟方法中的模型常数,达到能谱截断波数的改变,考察它对各向同性湍流计算的能谱以及能谱截断处小尺度涡能量积累问题的影响.
湍流;能量耗散;能谱分析
随着计算机硬件水平的不断提高和并行技术的日渐成熟,大涡模拟(LES,Large Eddy Simulations)方法在近年来取得了快速发展,并已逐步在部分工程湍流流动的模拟中得到了成功应用.然而,对于高雷诺数壁湍流,如果要保证能够正确分辨近壁区的湍流拟序结构及其演化过程,LES所需的计算规模仍嫌过高.针对这一问题,已有大量对近壁区的简化建模及方法研究,其中以RANS(Reynolds-Averaged Navier-Stokes)和LES的混合法[1]在工程湍流模拟中最具潜力.在RANS/LES混合方法中,脱体涡模拟方法(DES[2],Detached Eddy Simulation)、以及在其基础上衍生发展的Delayed DES(DDES) 方 法[3]和 Improved DDES(IDDES)方法[4]等,因其可实现近壁区 RANS和远离壁面LES的自动切换,易于在工程流动的模拟中应用,从而获得了很高的关注,并已有相当多的研究已证明了该方法在一些与壁面边界层相关性不大、并且存在大尺度分离或自由剪切层的工程湍流流动的模拟中能够获得高质量的结果.
另一方面,尽管LES以及DES方法的理论基础已逐步得到了完善,但其数值方面的问题目前仍是阻碍其取得进一步发展和应用的主要障碍之一,具体而言,是计算网格和离散格式的问题,并且在一定程度上两者是相关的.通常,LES需要使用高阶精度的时间和空间离散格式,以确保格式的数值耗散水平不会淹没物理的亚格子粘性.而在工程中常见的流动问题中,几何计算域往往相当复杂,对于结构化网格,网格的质量难以较好地保证,并且边界条件也很难做到高阶精度,这时高阶格式的实际精度会大打折扣.所以,从工程实用和通用性的角度而言,成熟的、基于RANS的离散格式更具吸引力.本文的主要目的就是通过对各向同性湍流的DES模拟,对几种对流通量离散格式的适用性及亚格子尺度的选择等问题进行考察,为使用 DES研究工程实际流动问题打下基础.
本文所采用的各向同性湍流的参考数据为文献[5]于1971年所发表的实验测量结果.下面首先介绍DES方法及数值格式,其次给出各向同性湍流定解条件及初场的生成方法,然后对模拟结果进行讨论,最后为结论.
1 DES方法及数值格式
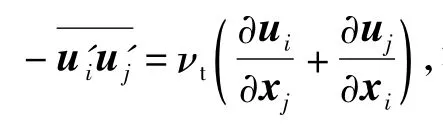
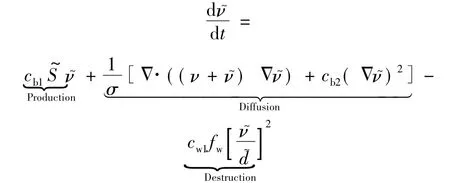
模型方程中的长度尺度定义为
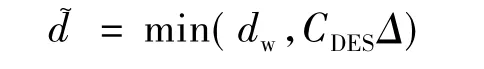
式中,dw为 RANS尺度;CDESΔ为 LES尺度;Δ=max(Δx,Δy,Δz);CDES为模型常数,可在数值模拟中加以调整.
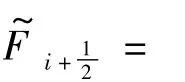
二阶中心差分格式:
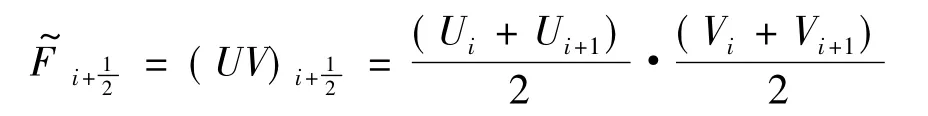
四阶偏斜对称型中心格式[6]:
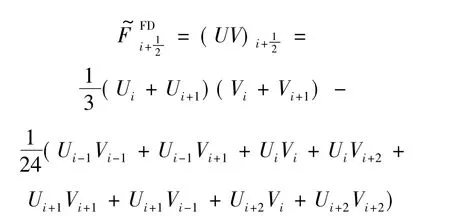
需要说明的是,以上给出的四阶偏斜对称格式是有限差分形式的,文献[6]也给出了基于有限体积离散的计算格式,但数值实验表明,采用有限差分形式的格式时计算稳定性更好,尤其是计算某些具有复杂边界的流动问题.关于对流通量的定义,从物理的角度出发,应对对流通量中的输运项作如下分解:
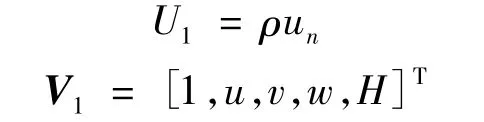
其中对流速度un=nxu+nyv+nzw.
而压力项则可分解为
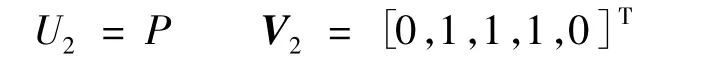
LDFSS格式是属于AUSM(Advection Upstream Splitting Method)类的迎风格式,格式构造的基本思想是认为流体的对流和声波的传播是两个物理上不同的过程,所以对于对流通量中的输运项和压力项应该分开处理,分别构造各自的分裂格式,具体参见文献[7].采用 MUSCL(Monotone Upstream-Centered Scheme for Conservation Laws)插值,可使格式精度达到三阶.需要说明的是,在MUSCL插值中未使用限制器,已有研究表明,如果在LES中使用限制器,则格式耗散太大.本文之所以对LDFSS进行测试,一方面是所发展的DES程序是基于使用该格式的原有RANS程序,另一方面则主要是考虑未来使用DES对跨音流动进行模拟时的计算稳定性和激波捕获问题,而LDFSS格式对这类流动是适用的.
2 定解条件及初场生成方法
本文使用均匀湍流的空间衰减实验结果验证DES数值模拟的准确性.按照泰勒假定,空间和时间之间可以互相转换,位移Δx和时间Δt之间的关系式为:Δx=UΔt.实验风洞中的湍流平均速度U是一个常数,而作数值模拟时湍流的平均速度为0,这相当于实验中在一个以速度U运动着的坐标系中去观察湍流场,它是随时间衰减的.实验中,基于格栅尺度的雷诺数 Re=U0M/ν=34000,入口速度 U0=10 m/s,格栅尺度 M=0.0508m,初始分子运动粘性系数 ν=1.494 m2/s.
实验测量的结果分别对应3个时间点:U0t/M=42,98和171.数值模拟时,将实验的第1个时间点U0t/M=42下的能谱作为计算初始T=0ms时刻的能谱,而另外两个时间点U0t/M=98和171则分别对应于数值计算中T=284.5ms和655.3ms时刻,通过对比这两个时刻的能谱分布,检验DES模拟的精确程度.
初始流场的正确与否直接关系到后续数值模拟的准确性与精度,初始流场的选择包括计算域、网格数、初始能谱函数以及其他性能参数的确定.
计算域取边长为L的立方体,3个方向上网格均匀分布,网格数均为N;均匀各向同性湍流中计算域尺度L即等于可求解的最大旋涡的尺度,即可分辨的最大旋涡的波数为能有效分辨的最小旋涡的波数为,式中为网格尺度.网格的疏密须保证惯性区域包含于可分辨的波数范围之内,即应当使惯性区域包含于[2π/L,πΔ]之内.
立方体内为粘性可压缩流体,初始脉动速度场满足谱空间连续方程和能谱约束方程[8].初始能谱函数分布需要与实验条件相吻合,与文献[9]中一致,可给定Von Karman波谱:
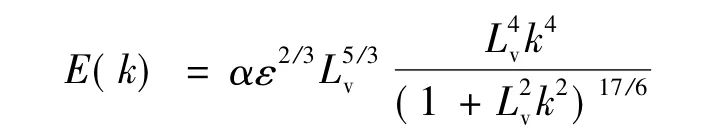
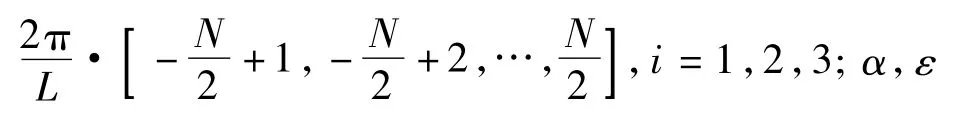

表1 Von Karman波谱参数
接下来,根据选定的初始能谱分布函数构造谱空间初始速度场,本文在构造初始谱空间速度场时,采用文献[10]所提出的构造方法:
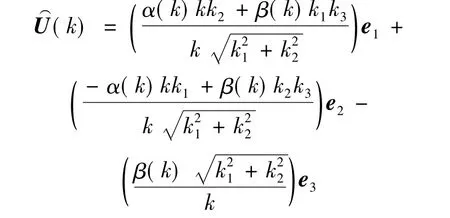
初始流场密度取为空气密度值1.2kg/m3,初始分子运动粘性系数取为ν=1.497×10-5m2/s,初始温度与运动粘性系数对应,流体满足理想气体状态方程.湍流输运方程中初始湍流运动粘性系数ντ(亚格子粘性系数)可用Smagorinsky湍流模型求得:|,其中,模型常数

图1 初始脉动速度场的能谱分布
在沿时间推进进行非定常求解时,边界条件取为在3个方向上的边界处均采用周期性边界条件.
3 数值模拟及结果分析
可能影响各向同性湍流DES模拟结果的主要有以下因素:截断波数的选取,对流格式的选择和CDES取值.下面将通过一系列算例来分析这些因素对数值模拟的影响,并确定最适合的选择.
计算域与网格数的选择决定了所能分辨的旋涡波数范围,下面给出两种波数截断情况的模拟结果,以考察数值方法的适用性.一种情况是截断波数在一半惯性子区范围,另一种是直接求解大部分惯性子区.计算域分别取边长L=1.0m和L=0.42m的立方体,网格数均为643,具体参数见表2.
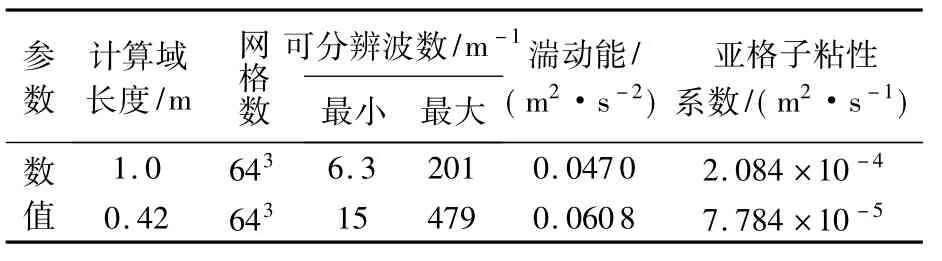
表2 初始流场参数
由表2可以看出,计算域为L=1.0m时,所能分辨的旋涡的波数范围是(6.3,201),截断波数为 kc1=201 m-1;当计算域缩小为边长 L=0.42m时,求解的波数范围增大,可分辨的波数为(15,479),截断波数为 kc2=479m-1,基本包含了整个惯性子区区域.
图2给出了DES模拟能谱与实验能谱的对比图,CDES均取值为 1.0.

图2 能谱对比图
图2a、图2c、图2e算例可分辨的旋涡波数范围在惯性区一半左右,两种中心型格式所模拟的能谱基本符合-5/3律,与实验结果吻合,表明格式耗散较小以及S-A模型模拟的准确性;迎风型格式则表现出较大的耗散性,在较高波数区域的能谱斜率比较陡峭.图2b,图2d,图2f算例可分辨的旋涡波数范围基本包含整个惯性子区,两种中心型差分格式仍能较好模拟整个惯性子区,迎风型格式由于耗散较大还是与实验能谱有些差异.以上结果说明对于所使用的计算网格规模,截断波数对于数值模拟结果影响不大,可根据实际需求进行选择可分辨的波数范围(旋涡尺度).数值试验证明,在数值稳定性方面,迎风型格式比中心型格式要好[11],但在LES模拟中,中心型格式在旋涡分辨以及计算精度方面更有优势.因此也有学者提出,在作脱体涡模拟的格式选取方面,RANS部分用迎风型格式而LES部分用中心型格式是一个合适的选择[12].
截断波数处能量积累是很多文献中都提到的现象,从图2中可以看出,中心型格式模拟的能谱在接近截断波数时,能谱值不是继续减小而是增大,这种和精确理论值及实验不符之处来自谱截断影响.湍动能在从大尺度涡传递给小尺度涡的过程中,在到达截断波数处时能量不能继续下传,同时湍动能耗散不足,便造成湍动能的积累[13].采用相同网格数时,雷诺数愈高,分辨率愈低,在截断波数附近的能量积累愈大,甚至可能导致计算发散.缓解能量积累的方法是增加高波数段的湍动能耗散,如采用超粘的方法,具体参见文献[14].另外,还可以改变截断波数,当发现截断波数处湍动能积累较大时,适当增大截断波数,扩大可解尺度范围.相比之下,迎风型格式耗散较大,加大了截断波数处湍动能的耗散,因此没有出现能量积聚的现象,但带来的是能谱斜率较实验能谱更陡.
CDES在DES方法中是用于调节截断波数的常数,随着CDES的增大,直接求解的最小旋涡尺度和亚格子应力模型模化的最大旋涡尺度会相应增大.下面对CDES取不同的值,查看它对数值模拟结果的影响,基准能谱为实验测量U0t/M=98时刻的能谱.
图3、图4的计算网格数为643,谱截断波数分别为 kc1=201m-1和 kc2=479m-1.可以看出,中心型格式在CDES值增大时,高波数区域能谱的斜率也增大.由图3能谱曲线可见,kc1=201m-1时二阶中心格式和四阶偏斜对称型格式的最佳CDES取值为0.9;同时,有数值实验可得截断波数为kc2=479m-1时,两种中心型格式的最佳CDES取值为1.0.两种不同截断波数情况下最佳CDES值均大致为1.0,并且随着CDES值变化都存在相似的能谱变化,这实际上是初场的生成所致.生成初场时,截断波数由计算域和网格决定,即kc=π/Δ.波数小于该截断波数的大尺度旋涡结构包含在初场中,而截断后的小尺度涡其效应则由Smagorinsky模型计算的亚格子涡粘初场体现.
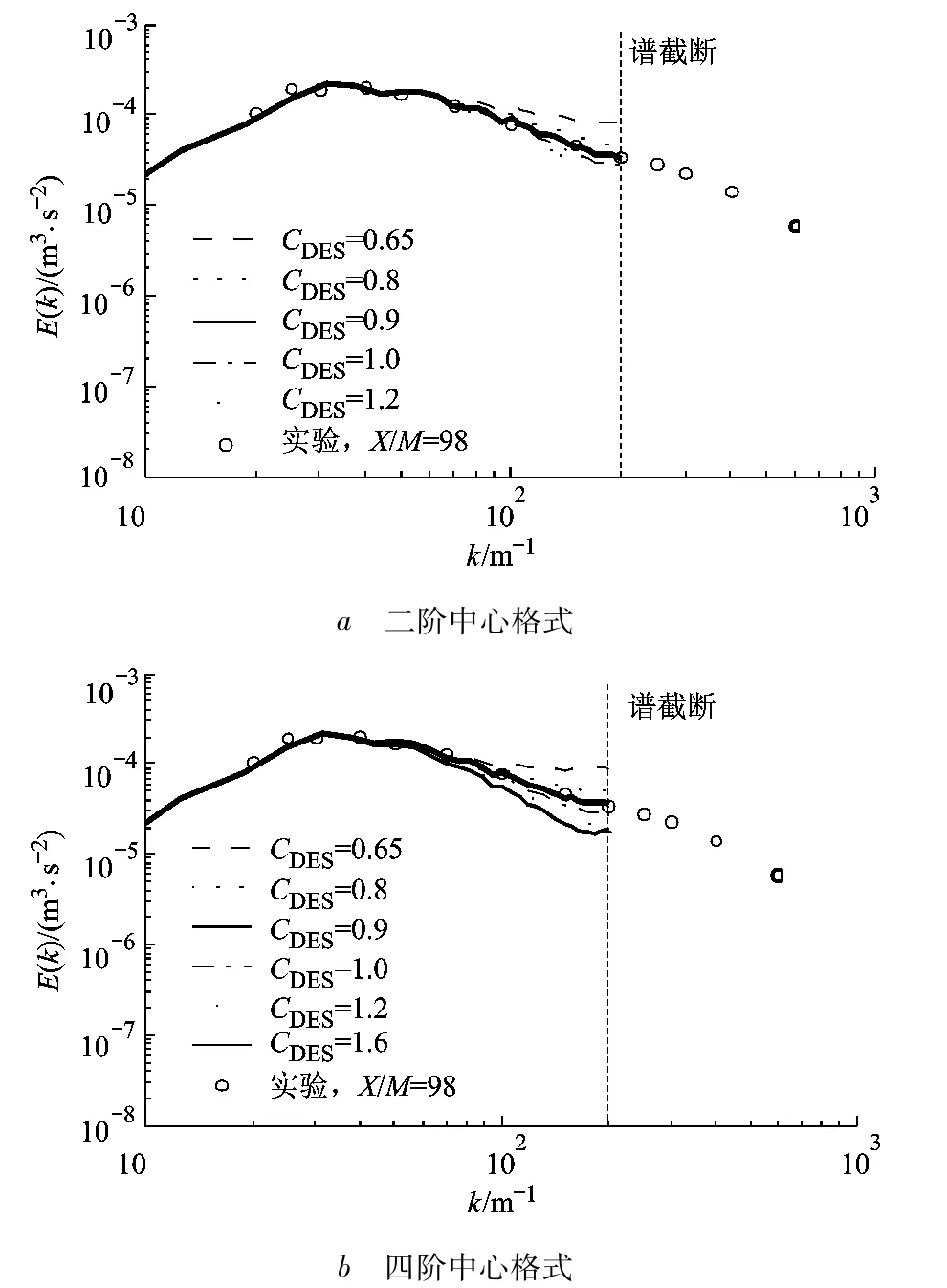
图3 kc1=201m-1时两种中心格式计算的能谱
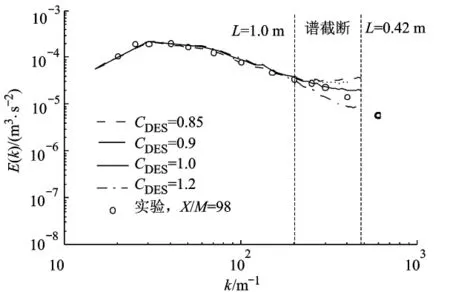
图4 kc2=479m-1时四阶中心格式计算的能谱
对于DES而言,亚格子尺度定义为CDESΔ,相应截断波数为 kc=π/(CDESΔ).CDES=1.0 时,其截断波数与初场给法一致;CDES>1.0时,截断波数小于π/Δ,计算的亚格子粘性偏大,因而减弱了截断波数附近的能量积累现象;反之CDES<1.0时,截断波数大于π/Δ,计算的亚格子粘性偏小,能量积累现象明显.由此可得,如果所关注的某段能谱范围(如kc1≤201m-1)其旋涡模拟出现能量积累(图3b),可以通过增大截断波数予以改善(见图4),而增大CDES值同样能予以改善.另外,本文CDES的最佳取值与有些文献中提到的最佳取值CDES=0.65[1]有所出入,这与本文的数值格式、初场生成以及特定算例有关,在今后的计算应用中应根据实际情况调整CDES取值.
对于迎风型格式,643网格下CDES值从0.1到2.0变化,其格式耗散使得能谱分布的斜率都比实验值要陡峭(见图5).而在相同CDES的情况下,网格较密的963网格数下计算的能谱要比643网格计算能谱更接近实验谱,说明用迎风型格式对计算网格密度有更高的要求.
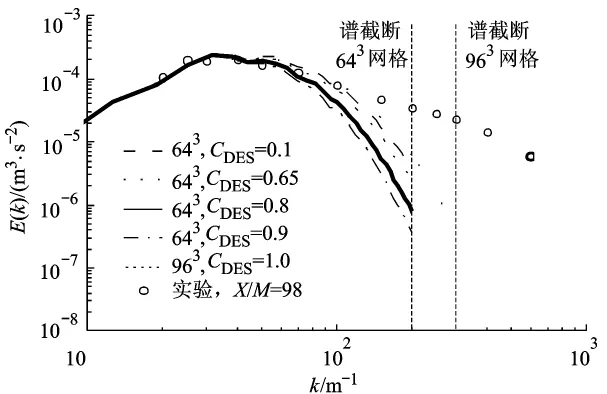
图5 LDFSS格式不同网格数和C DES值计算的能谱
4 结论
脱体涡模拟方法在近壁区用RANS模拟,在远离壁面区用LES模拟,集采二者之长,已逐渐成为一种应用广泛的数值模拟方法.本文采用基于S-A模型的DES方法,考察了二阶和四阶中心型格式、以及迎风型LDFSS格式这3种对流通量格式在均匀各向同性湍流模拟中格式的耗散性及DES模拟中计算网格、截断波数的选择等问题.
结果表明,虽然在MUSCL插值中并未使用会带来较大数值耗散的限制器,但LDFSS格式的耗散仍较大,使得在大波数区域分辨不足,但对截断波数附近能量积累现象有较好的消除;二阶中心格式和四阶偏斜对称格式能较好地模拟惯性子区能谱,满足-5/3律,耗散较小,但存在谱截断能量积累现象.另外,从结果中还可看到,以本文计算所使用的网格规模和选择的截断波数,二阶中心格式可获得与四阶偏斜对称格式几乎相同质量的解.
亚格子尺度由计算网格以及CDES的取值决定.对于CDES的取值,截断波数为kc1=201m-1时二阶中心格式和四阶偏斜对称格式的最佳取值为CDES=0.9;截断波数为 kc2=479m-1时它们的最佳取值为CDES=1.0;计算网格尺寸的调整意味着对谱截断波数的调整,增大谱截断波数对于改善能量积累有一定的作用,同时对低波数范围的能谱模拟没有影响,因而可根据实际情况选择可分辨的波数范围.
References)
[1] Schumann U.Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli[J].Journal of Computational Physics,1975,18:376 -404
[2] Spalart PR,Jou W H,Stretlets M,et al.Comments on the feasibility of LES for wings and on the hybrid RANS/LES approach[C]//Liu C,Liu Z.Proceedings of the 1st AFOSR International Conference on DNS/LES.Colombus:Greyden Press,1998:137 -147
[3] Spalart PR,Deck S,Shur M,et al.A new version of detachededdy simulation,resistant to ambiguous grid densities[J].Theoretical and Computational Fluid Dynamics,2006,20:181 -195
[4] Shur M L,Spalart PR,Strelets M K,et al.A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J].International Journal of Heatand Fluid Flow,2008,29(6):1638-1649
[5] Comte-Bellot G,Corrsin S.Simple Eulerian time correlation of full- and narrow-band velocity signals in gridgenerated‘isotropic'turbulence[J].Journal of Fluid Mechanics,1971,48:273-337
[6] Ducros F,Laporte F,Souleres T,et al.High-order fluxes for conservative skew-symmetric-like schemes in structured meshes:application to compressible flows[J].Journal of Computational Physics,2000,161:114 -139
[7] Liou M S.A sequel to AUSM:AUSM+[J].Journal of Computational Physics,1996,129:364 -382
[8] Frisch U.Turbulence:the legacy of A.N.kolmogorov[M].Cambridge:Cambridge University Press,1995
[9] Mann J.Wind field simulation[J].Probabilistic Engineering Mechanics,1998,13(4):269 -282
[10] Rogallo R S.Numerical experiments in homogeneous turbulence[R].NASA-TM81315,1981
[11] Travin A,Shur M,Strelets M,et al.Physical and numerical upgrades in the detached-eddy simulation of complex turbulent flows[J].Fluid mechanics and Its Applications,2004,65(5):239-254
[12] Hansen A,Sorensen N N,Johansen J.Detached-eddy simulation of decaying homogeneous isotropic turbulence[R].AIAA-2005-885,2005
[13]张兆顺,崔桂香,许春晓.湍流大涡数值模拟的理论和应用[M].北京:清华大学出版社,2008:137-141 Zhang Zhaoshun,Cui Guixiang,Xu Chunxiao.Theoretics and applications of large eddy simulations in turbulence[M].Beijing:Tsinghua University Press,2008:137 -141(in Chinese)
[14] Lesieru M,Metais O,Comte P.Large-eddy simulations of turbulence[M].Cambridge:Cambridge University Press,2005
(编 辑:文丽芳)
Detached eddy simulation of homogeneous isotropic turbulence
Wu Jingfeng Ning Fangfei
(School of Jet Propulsion,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Detached eddy simulation was used to simulate decaying homogeneous isotropic turbulence.Simulation results were compared to the experimental data of Comte-Bellot and Corrsin,showing that the detached eddy simulation of homogeneous isotropic turbulence was acceptable.The method proposed by Rogallo was used to construct the initial velocity field and the generated turbulence field fit the Von Karman spectrum.In the choosing of convective flux scheme,second-order centered scheme and fourth-order skew-symmetric scheme and upwind low-diffusion flux-splitting scheme were used respectively to check the numerical dissipation and suitability in the detached eddy simulation of homogeneous isotropic turbulence.Meanwhile,the cutoff wave number was changed with the varying of computational region and turbulence model parameters.In this way,the simulation results shows how energy spectra and energy accumulation for small scales are influenced by the variety of the cutoff wave number.
turbulence;energy dissipation;spectrum analysis
V 211.1
A
1001-5965(2011)05-0589-06
2010-04-20
国家自然科学基金资助项目(50506001)
吴晶峰(1983-),男,博士生,江西鹰潭人,buaawjf@sohu.com.

