三相变四相电力变压器模型与实验研究

刘光晔，江 睿，邹 宇

0 引言

在电气化铁路牵引供电系统中，通过三相变两相平衡牵引变压器供电，可以抑制负序电流对三相电力系统的影响。如果进一步采用高电压、大容量AT（自耦变压器）牵引供电系统，则必须增加2台自耦变压器。最早的三相变两相平衡变压器出现于20 世纪20 年代，接线方式为T 形耦合接线，或称斯科特（Scott-Teaser）变压器。随着电气化铁路发展的需要，到20 世纪70 年代已经形成了系列的平衡变压器接线方案。在众多的平衡变压器接线方案中，从本质上看，最基本的只有如下3 种类型，即斯科特变压器、李布郎克（Le Blanc）变压器与伍德桥（Wood Bridge）变压器，而其他方案均可由这3 种变压器派生而来[1]。

四相输电系统是最接近三相的多相系统，该系统能大大提高输电线路的输送功率密度，既具有多相输电方式的优点，又克服了多相输电所存在的缺点[2]。四相输电系统应用的重大关键设备是研究与实施三相变四相及其逆变换的电力变压器。三相变四相电力变压器用于电气化铁路AT 牵引供电系统，可节省2 台自耦变压器，既节约了成本，又节省了占地面积[3，4]。原则上，在平衡变压器的两相侧采用增加一套副绕组的双重接线方案，便可得到三相变四相电力变压器。而事实上，平衡变压器单柱绕组数目较多，平衡条件要求各绕组阻抗关系严格，设计制造要求较高[5～7]。如果采用双重接线方案，则单柱绕组数目增加近一倍，实施时，满足平衡条件则更加困难，甚至使绕组在空间布置上产生矛盾，无法达到各相参数平衡的要求。故此，国内外尚无研究三相变四相电力变压器的成功经验。

文献[8]首次构成了一种四相四心柱结构的三相变四相电力变压器，提出了三相变四相电力变压器的接线方案。该变压器的每相铁心柱上绕组不超过3 个，是不等相变换的最简单形式，它与现有的各类平衡变压器比较具有更多的优越性。本文建立了该变压器的数学模型，分析了其各绕组阻抗的相互关系，提出并证明了设计三相变四相变压器时，绕组阻抗须满足的中性点接地条件与平衡条件。设计制作了三相变四相电力变压器实验模型，验证了所提出的绕组阻抗关系理论的正确性。

1 三相变四相电力变压器的基本原理

三相变四相变压器采用四相四心柱式铁心，每相均有3 个绕组[8]，绕组接线如图1 所示。

图1 三相变四相电力变压器接线原理图

设三相侧的相电压与四相侧的相电压之比k =UA/Ua。取各相绕组的匝数关系为Wa1/Wa3= k、Wa2= Wa1/2、Wb1= Wb2= Wa1/2、Wa1= Wc1、Wa2= Wc2、Wb1= Wd1、Wb2= Wd2、Wa3= Wb3= Wc3= Wd3。由每相铁心磁势平衡的原理，原副边的电流变换关系：

根据式（1），当三相侧电流对称时，四相侧电流也对称。

2 三相变四相电力变压器的数学模型

三相变四相电力变压器接线原理如图1 所示。同一铁心柱上各绕组的同名端方向均用箭头方向标注。各绕组的等值阻抗、电流、电压均已统一折算到相绕组Wb3的匝数。另外，各绕组的阻抗、电流、电压符号中的下标分别与相应的绕组符号对应。三相侧各绕组的电流、电压参考方向均与绕组同名端的箭头方向相同。四相侧各绕组的电压方向与绕组同名端的箭头方向相同，但电流方向与绕组同名端的箭头方向相反。考虑到绕组a 相与c 相对称，b 相与d 相对称，有Zwa1= Zwc1、Zwa2= Zwc2、Zwa3= Zwc3、Zwb1= Zwd1、Zwb2= Zwd2、Zwb3= Zwd3。

对每个铁心柱上的三绕组变压器，可以求出各对绕组之间的电压降：

又各并联支路的电压相等，有：

忽略励磁电流，有磁势平衡方程：

设四相侧任意负载阻抗分别为ZLa、ZLb、ZLc、ZLd，同样已折算到相绕组Wa1的匝数，则：

由各绕组的匝数比例关系，三相输入电流和输入电压的实际值分别为

节点M 的电流方程为

其中三绕组变压器等值电路中的各绕组等值阻抗按如下方法计算

式（2）—式（8）即为三相变四相变压器的数学模型。通过直接求解数学模型，不仅可以计算平衡变压器在各种短路及运行情况下，变压器各绕组的电流分布；还可以考虑绕组阻抗存在设计误差与制造误差时，分析变压器运行特性的变化情况。通过对非理想参数平衡变压器特性进行仿真分析，可以详细讨论不同的绕组阻抗变化对变压器零序电流与负序电流的影响，为设计制造变压器确定绕组阻抗时应优先控制的参数误差提供理论指导。

下面再进一步讨论方程组的数目与变量的数目。式（2）—式（8）联立方程组总计27 个方程。每一个绕组均有电流和电压2 个变量，有12 个绕组24 个变量，加上3 相输入电流和3 相输入电压，总计30 个变量。如果已知三相侧电源的3 相输入电压，则方程组即可求解，也就是说，变压器的运行状态可以完全确定。如果变压器三相侧中性点O不接地，那么只能已知电源输入的2 个独立的线电压，此时可增加中性点O的节点电流方程IA+ IB+ IC= 0，方程组亦可求解。

3 变压器的绕组阻抗关系

变压器在正常运行情况下，四相侧负载阻抗相等时，要求三相侧电流对称；四相侧负载阻抗任意不相等条件下，三相侧仍无零序电流。为此，在设计制造变压器时，各绕组之间的阻抗关系必须满足严格的条件。下面进一步分析该变压器的中性点接地条件和三相（或四相）输入阻抗的平衡条件。

3.1 中性点接地条件分析

将式（3）—式（6）代入式（2），假定中性点不接地，考虑IA+ IB+ IC= 0 或(Ia1- Ic1) = 2(Ia2-

I

c2)，并令：

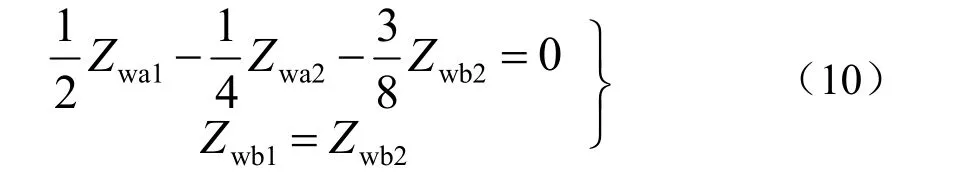
则有 UAO+ UBO+ UCO= 0

于是，只要满足式（10），就有UAO+ UBO+UCO= 0，即变压器三相电压的零序分量（中性点O的电压）为0。所以，当三相侧输入三相对称电压时，如果变压器中性点不接地，四相侧带任意不对称负载，中性点O 的电位始终为0，是一虚地点。也就是说，在设计制造变压器时，只要各绕组的等值阻抗满足式（10）确定的约束条件，则中性点悬空的电位始终不会发生偏移。此时如果中性点直接接地，也不会产生零序电流。故称式（10）为该变压器的中性点接地条件。将式（9）代入式（10），中性点接地条件可以进一步表达成如下每对绕组之间的阻抗约束关系：

3.2 三相输入阻抗平衡条件分析

当四相侧各相负载阻抗相等，即ZLa=ZLb= ZLc= ZLd= ZL时，并考虑到已满足式（10）中性点接地条件中的ZWb1= ZWb2，并令：

则ZA- ZB= ZA- ZC= 0。故式（12）即为变压器三相输入阻抗平衡的条件。根据变压器的可逆原理，如果在三相侧接三相对称负载，则四相侧的各相输入阻抗亦平衡。将式（9）代入式（12），平衡条件可以进一步表达成如下每对绕组之间的阻抗约束关系：

3.3 绕组布置的实施方案

根据绕组阻抗的约束条件，简要讨论变压器绕组布置的实施方案。在a 相铁心柱上，因为绕组Wa2的匝数只有绕组Wa1的匝数的一半，为了使绕组之间偶合紧密，将绕组Wa2布置在绕组Wa1与绕组Wa3的中间。根据式（11），要求在b 相铁心柱上，绕组Wb1与Wb2的布置具有对称性，故此Wb1与Wb2可以考虑采用交叉绕组的布置方案。显然，由于Wb1与Wb2采用对称交叉分裂形式，故式（10）的第二式便自然得到满足。变压器绕组布置方案见图2。

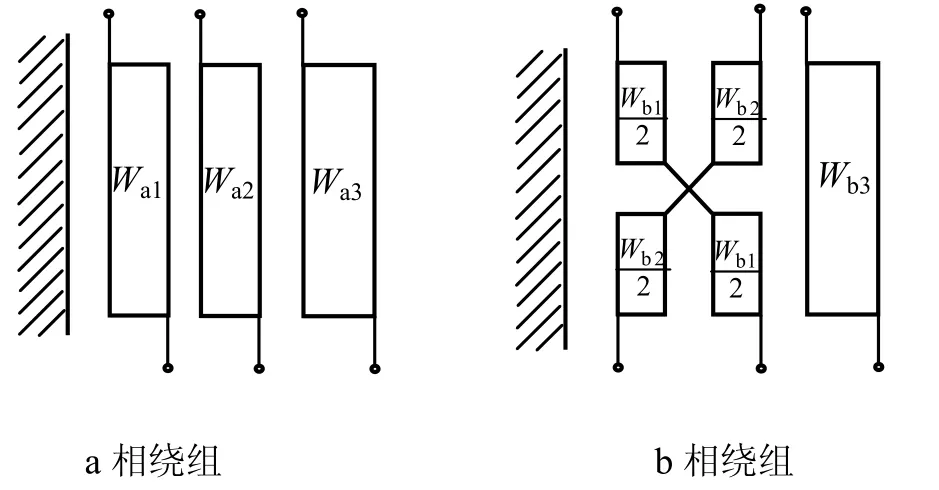
图2 平衡变压器a 相、b 相绕组布置图

4 模型实验验证

为了验证本文提出的变压器绕组阻抗约束条件以及变压器模型的正确性，设计制作了1 台变压器模型。变压器铭牌参数为，SN= 800 V·A，400/230 V，VS% = 10.5，ZS= 21 Ω。各绕组短路阻抗测试值见表1。值得注意的是，在变压器模型设计中，由于绕组阻抗值中的电阻部分较大，必须计及其对变压器短路阻抗的影响。

表1 各绕组短路阻抗实验结果数据表

定义|ΔO|%为不满足中性点接地条件式（11）的误差与短路阻抗ZS之比，定义|ΔP|%为不满足平衡条件式（13）的误差与短路阻抗ZS之比。对该变压器进行短路试验、额定负载（cosφ = 1.0）试验与半载试验，结果见表2。表2 中，I0/I1、I2/I1分别表示零序电流、负序电流与正序电流的比值，它们体现了三相侧电流的不对称度。

前面理论证明，如果|ΔO|%≠0，则短路试验三相侧有零序电流；如果|ΔP|%≠0，则短路试验三相侧有负序电流。由表2 可以看出，|ΔO|%与|ΔP|%越大，短路试验时三相侧的零序电流与负序电流越大。当负载达到额定值时，零序电流不变，而负序电流显著减小，这证实了零序电流与变压器的负载阻抗无关，负序电流的大小主要由负载阻抗的大小及其是否对称决定。在分析中性点接地条件的过程中，中性点不接地时的零序电压与中性点接地条件的误差量成正比，表明零序电流与|ΔO|%成正比。再来讨论如何优先满足变压器绕组阻抗设计的约束条件。尽管平衡条件误差大于中性点接地条件误差（|ΔP|%＞|ΔO|%），可是随着负载阻抗的增大，负序电流显著减小。当由短路试验达到额定负载时，负序电流已变得很小，而零序电流的相对值始终维持不变。所以，根据以上分析，在设计平衡变压器的阻抗约束关系中，应优先满足中性点接地条件的要求。

表2 短路试验与额定负载试验结果数据表

根据变压器中性点接地条件与平衡条件，在设计各对绕组之间的短路阻抗时，可以分析各对绕组之间的短路阻抗设计值对运行特性影响的灵敏性。在式（11）中各个阻抗值前面的系数为该绕组阻抗对零序电流影响的灵敏度系数；在式（13）中各个阻抗值前面的系数则为该绕组阻抗对负序电流影响的灵敏度系数。

5 结论

（1）建立了三相变四相变压器的数学模型，通过求解数学模型，不仅可以计算平衡变压器在各种短路及运行情况下，变压器各绕组的电流分布，还可以考虑绕组阻抗存在设计误差与制造误差时，分析变压器运行特性的变化情况。

（2）分析设计三相变四相变压器时，绕组阻抗必须满足的中性点接地条件式（11）与平衡条件式（13）。当满足中性点接地条件时，变压器任意运行状态三相侧无零序电流。当满足平衡条件时，变压器短路试验三相侧输入阻抗平衡。

（3）模型实验表明，中性点接地条件相对误差|ΔO|%与平衡条件相对误差|ΔP|%越大，短路试验时三相侧的零序电流与负序电流越大。在设计平衡变压器必须满足的阻抗约束关系中，应优先满足中性点接地条件的要求，为如何控制平衡变压器参数的设计误差提供了理论指导。

（4）制作的三相变四相变压器的试验模型验证了该种变压器的可行性。模型实验表明，变压器在正常运行条件下，三相侧仅存在很小的零序电流与负序电流。

[1] 刘光晔，周先哲，湛春晖，等.四相输电及其电力变压器原理[J].电工技术学报，2005，20（4）：9-14.

[2] 刘光晔，杨以涵.新型四相架空输电线路研究[J].电工技术学报，1999，14（2）：73-76.

[3] 高仕斌，钱清泉.电气化铁道应用三相变四相电力变压器的理论分析[J].中国电机工程学报，2004，24（3）：174-177.

[4] 娄奇鹤，高仕斌.三相变四相变压器在AT 供电系统中的应用研究[J].中国电机工程学报，2005，25（1）：124-130.

[5] 肖乐军，刘福生，黄梅.阻抗匹配平衡变压器运行特性研究的数学模型及实验验证[J].电工技术学报，1993，8（4）：11-15.

[6] 陆家榆，陈莉，丁青青.YN/∀联结平衡变压器运行特性的数学模型[J].中国电机工程学报，1998，19（5）：345-349.

[7] 吴命利，范瑜.星形延边三角形接线平衡变压器的阻抗匹配与数学模型[J].中国电机工程学报，2004，24（11）：160-166.

[8] 刘光晔.三相变四相电力变压器的接线方案与原理研究[J].中国电机工程学报，2000，20（1）：81-84.