透明塑料板件注射-压缩成型模拟研究

李毅超, 张宜生, 李德群

(华中科技大学材料成形与模具技术国家重点实验室,武汉 430074)

大型透明板件在航空、汽车等工业制造领域的应用越来越广泛[1,2]。这类制件由于其特殊应用领域的要求必须具备质量轻,强度高,光学性能良好等优点。通过对相似大型平板件进行的模拟与光学畸变测量结果分析来看,制件在边角部分的残余应力与收缩不均是影响其制造质量的最主要原因[3,4]。而注射过程中熔体较长的纤维流线与不均等的温度变化会产生较大的残余流动应力与残余热应力[5],在熔体快速冷却过程中被“冻结”在熔体内成为残余应力与收缩的主要来源。而注射-压缩成型方法(Injection-Compression Molding)可以较好的解决这一问题。由于在注射末尾阶段添加压缩过程,有利于控制熔体表面压力分布均等,从而从根本上消除制件残余应力与收缩不均的问题。

近几年,国内外对此项技术进行了大量研究。Fan等[6]使用非等温可压缩流动模型,通过有限元和有限差分相结合的方法对注射-压缩成型进行了模拟。计算结果与实验结果在模温,熔化温度和保压方面得到较好的一致性。Bickerton等[7]对注射-压缩过程中的压缩速度与压紧力进行了研究。结果表明,通过增大压紧力或对模具施加内应力,合理调整压缩速度与初始型腔厚度可以显著降低注射时间。Chang等[8]通过在定模模底添加纤维加固层的方法对树脂的注射-压缩工艺进行了试验分析。结果显示,较小的模具张开距离和较高的压缩速度能够降低注射时间,提高制件质量。Chen等[9]研究了透明件在注射-压缩工艺条件下成型后的双折射现象,并与传统的注射成型结果进行了比较。结果表明,注射-压缩工艺比传统方法能显著地减少制件的双折射现象,且相对延长保压时间,提高保压压力能降低制件双折射的产生。

本研究通过采用水平集、动量方程与能量方程进行多物理场全耦合计算的方式,对非对称几何透明塑料板件的注射-压缩成型过程进行了模拟分析,重点研究了成型过程中纤维流线与温度对制件收缩率的影响,并与传统的注射结果进行了比较。其目的是为深入研究应用模拟技术,改善注射-压缩工艺,探索控制成品质量的途径,以指导工程应用。

1 数学建模与算法

1.1 几何模型与基本假设

计算几何模型如图 1所示,模型呈等厚度 L型非对称结构。设计该模型的目的是为了便于检验注射或注射-压缩过程中,材料沿着等截面、规则转角及均匀收缩变截面流动过程中材料的流动状态,进而分析其对成形质量,特别是厚度方向收缩的影响。注射材料为聚碳酸酯(PC)。

模拟过程中进行如下假设：1)在注射过程中不考虑熔体Z方向流动且型腔压力不随Z方向变化; 2)模拟过程中腔内气体密度与粘度设定为常数;3)模拟过程中不考虑壁面与外界传热并且设定入口与壁面温度为常数。

图1 透明平板件模型Fig.1 Transparent panelmodel

1.2 控制方程

模拟过程中采用水平集方法(Level-Set Method)追踪流体流动前沿。Φ是一个在 0～1平滑变化的连续函数,表示界面位置。Φ=0表示空气,Φ =1表示熔体,Φ=0.5表示熔体与空气界面,即流动前沿。Φ由方程(1)进行求解。

参数 ε用来描述边界的厚度。γ用来控制 Φ的稳定性。模拟过程中将水平集方法耦合进N-S方程对流体的运动求解,同时由能量方程对温度的变化进行求解,其公式如(2)～(4)所示。

式中u,v为熔体在x,y方向速度分量;ρ为密度;p为压力;η为粘度;σ为表面张量系数;K为界面曲率;Cp为热容参数;k为传导参数;h为模具热传系数;Tw为模具温度;γ﹒为流体剪切速率。由于使用了水平集方法,控制方程的密度 ρ,粘度η,热容参数Cp与传导参数k按公式(5)进行计算,其中下标 1表示空气参数,下标 2表示熔体参数。

模拟过程中所用材料选自PC系列,牌号为Calibre5100。熔体为粘度变化的非牛顿流体,采用(6)所示Cross-WFL粘度模型进行计算。

式中 n为非牛顿指数,η0为零剪切粘度,¯γ为流体剪切速率,τ＊为材料参数,数值如表 1所示。

表1 PC材料工艺参数Table 1 Parameters of PC

1.3 全耦合非线性数值算法

由N-S方程对流动过程计算得到熔体速度值。将其带入水平集方程求解得到熔体界面位置值,同时将速度值带入温度场方程求解得到熔体温度值,如此循环直到结束。同时材料粘度随剪切速率呈非线性变化。流动过程中,熔体与壁面接触发生对流换热过程,温度随时间也呈现非线性变化。针对全耦合非线性过程,采用多物理场耦合求解平台软件COMSOL 3.5进行求解。

1.4 边界条件设定

如图 2所示,对于流体方程,在注射过程中,入口处(Γinlet)定义为恒定熔体流进的层流流入边界条件;在压缩过程中,入口定义成封闭的壁面条件。壁面处(Γwall)流体经过的壁面为无滑动边界条件,而空气占据的壁面定义为滑动边界条件。在注射过程中,出口处(Γoutlet)定义为零压力出口;在压缩过程中,出口定为壁面条件。对于温度方程,在注射过程中,入口处(Γinlet)定义为温度边界条件 T= 300℃;在压缩过程中,入口定义为封闭热绝缘层。壁面和出口全部定义为热绝缘层。

图2 模型边界条件及变量参数Fig.2 Boundary conditions and parameters

2 结果与讨论

2.1 注压工艺与注射工艺收缩率比较

注射-压缩工艺较传统注射工艺能够显著降低制件收缩率。计算过程中设定的注射时间为 1.5s,压缩时间为 1s。注射阶段制品厚度方向模具高度为0.02m。注射结束,压缩阶段模具在板料厚度方向的压缩行程的速度为 0.01m/s。图 3中可以看出,在注射成型结束后制件收缩率呈现不均匀分布,最大收缩率为 4.9%;而从图4中的等值线分布可以看出,在注射-压缩成型工艺下制件收缩较为均匀,最大收缩率下降到3.4%。从而可看出注射压缩成型与注射成型相比,最大收缩率下降了 1.5%左右,并且分布更为均匀。

图3 常规注射填充时制品收缩率等值线图Fig.3 Contour graph of shrinkage on injectionmolding

2.2 纤维流线对收缩率的影响

图4 注射填充量达到90%时压缩1s制件收缩率等值线图Fig.4 Contour graph of shrinkage on the case of 90% injection volume and 1s compression

型腔内各结点的纤维流动长度会对制件成型过程中残余应力的产生起到影响,纤维流线的长短决定着由其产生的残余流动应力的大小[10]。从图 5可以看出,型腔内各区域的结点在注射过程中被显著拉长,并且长度不一,分布不均匀。而从图 6可看出,在注射-压缩工艺下,结点的位移量相对较短,并呈现区域性的长度一致。图7可以看到,型腔不规则的几何结构会对流体的运动产生影响,在转角与变截面处由于熔体的堆积导致压缩过程中区域 3, 4,5产生较大结点位移。结点运动的长短可以显示出熔体纤维流线的变化情况。注射工艺中产生的较长而不均等的纤维流线会产生流动剪切应力,在冷却过程中被“冻结”在熔体内部形成残余流动应力,最终引起制成件残余应力、收缩率等缺陷的产生。而注射-压缩成型工艺产生的纤维流线相对较短且均匀,这样可以减小残余应力的产生,并使其收缩率分布均匀,最终达到提高制件质量的目的。

图5 常规注射填充结束时结点运动轨迹图Fig.5 Track graph ofnodesmoving on injectionmolding

2.3 型腔温度对收缩率的影响

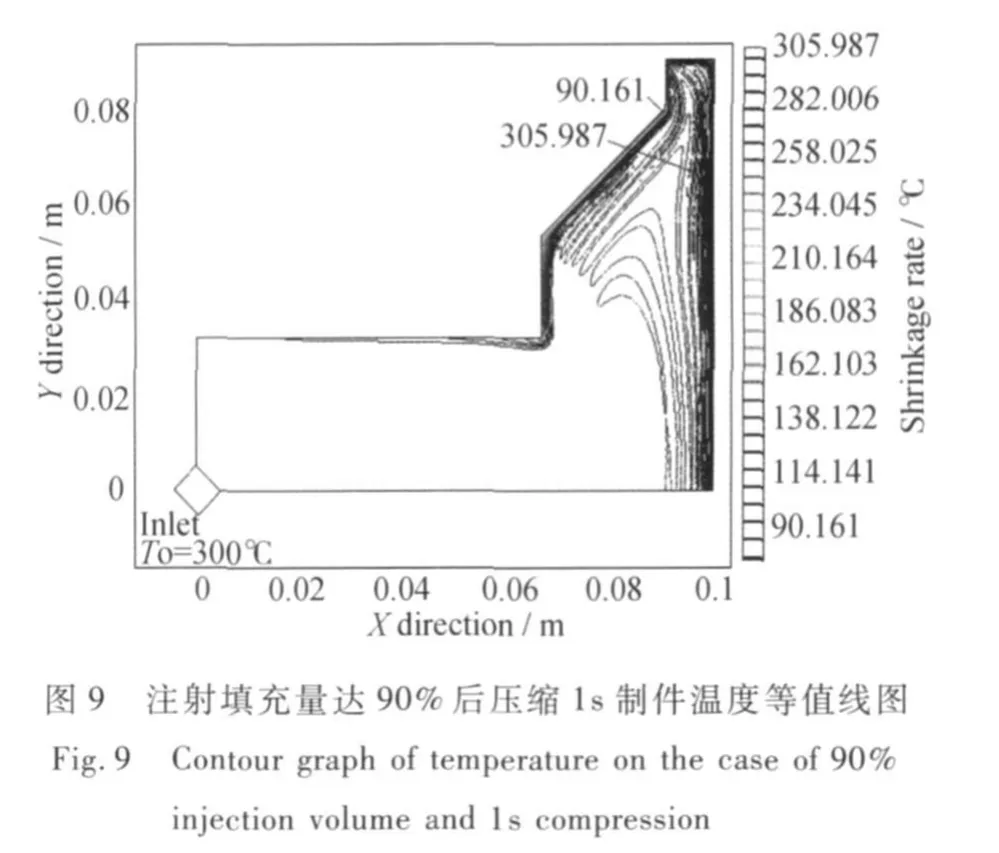
型腔内的温度变化也会对制件的收缩率产生影响,成型结束时温度越低,分布越均匀,产生的残余热应力就越小,制件收缩率也随之下降。从图 8可以看出,注射成型结束时熔体的最高温度接近350℃且分布不均。从图 9可看出,熔体的最高温度为 305℃,较注射成型下降了45℃,而且温度分布逐渐均匀。相应的制件收缩率也从图3中的4.9%下降到图4中的 3.4%。在图 8中,由于熔体快速填充型腔并与较冷的壁面产生不均匀接触,使得一方面,型腔内保持了较高的温度;另一方面,熔体在壁面处产生不均匀的温度变化,这将导致熔体粘度的不均等变化,从而阻碍熔体在型腔中的运动,影响其纤维流动,增大了制成件的收缩率。在注射-压缩工艺下,由于压缩的挤压作用,熔体会与壁面、模具表面产生充分接触,从而腔内温度大幅度下降,并且均匀分布。这样可以保持熔体在型腔内的均匀流动,使其纤维流线均匀化,从而减小制成件的残余热应力与收缩率。

3 结论

(1)注射-压缩成型工艺较传统注射成型工艺相比能够显著降低制件收缩率(4.9%降低到3.4%),并使其分布更均匀。

(2)成型过程中,熔体的纤维流线长度与温度是影响制件收缩率的两个重要因素。较短的纤维流线长度与较低且均匀的型腔温度能够减小制件残余应力与收缩率的产生,达到提高制成件质量的目的。

(3)对于不规则几何形状制件的成型,由于熔体在转角与变截面处流动受阻产生堆积现象,压缩过程会引起熔体不同区域纤维流线的不均匀拉伸,影响制成件质量。所以注射-压缩工艺更适用于制造对称形状的制件。

[1]史国力,李复生,田红兵.聚碳酸酯在汽车和航空透明材料领域应用的研究进展 [J].材料导报,2006,20(5)：404-407.

[2]王磊,史伟琪.直接成形的无骨架飞机透明件 [J].航空制造工程,1997,(10)：13-15.

[3]陈宇宏,袁渊,张宜生,等.基于光学畸变要求的注射成型透明平板应力翘曲分析 [J].航空材料学报,2008,28 (6)：82-87.

[4]李毅超,朱彬,张宜生.透明塑料平板厚向收缩及光学畸变研究[J].塑料,2009,38(5)：108-110.

[5]黄峡宏,余敏强,周持兴.聚合物注塑残余应力研究进展[J].力学进展,2000,30(2)：272-281.

[6]FAN B F,KAZMER D O.Simulation of Injection Compression Molding for Op tical Media[J].Polymer Engineering and Science,2003,43(3)：596-606.

[7]BICKERTON S,ABDULLAH M Z.Modeling and evaluation of the filling stage of in jection/comp ression moulding [J].Composites Science and Technology,2003,63：1359 -1375.

[8]CHANG Chih-yuan.Simu lation ofmold filling in simultaneous resin injection/compression molding[J].Journal of Reinforced Plastic and Composites,2006,25：1255-1268.

[9]CHEN Shia-chung,Chen Yung-cheng,Peng Hsin-shu,et al.Simulation of injection compression molding process, Part3：Effect of process conditions on part birefringence [J].Advances in Polymer Technology,2002,21(3)：177 -187.

[10]ISAYEV A I.Injection and comp ression molding fundamentals[M].USA：Library of Congress,1987：264-265.