剪切褶皱薄膜动态特性分析
李云良,鲁明宇,谭惠丰,谭忆秋
(1.哈尔滨工业大学交通科学与工程学院,150090哈尔滨,liyl-hit@163.com;2.哈尔滨工业大学土木工程博士后流动站,150090哈尔滨;3.香港理工大学机械工程学院,香港;4.哈尔滨工业大学复合材料与结构研究所,150001哈尔滨)
在薄膜结构中,由于薄膜的抗弯刚度很小,所以往往有褶皱存在[1-2].褶皱将影响到薄膜的稳定性及其应力分布,而且还会对薄膜的动态特性产生一定的影响[3].目前对于薄膜褶皱的形成及扩展规律进行了广泛研究[4-6],而对于薄膜产生褶皱后的动态特性的研究则相对较少.
Kukathasan等[7]对具有褶皱薄膜的自振特性进行了数值模拟分析.对薄膜褶皱的处理采用了迭代薄膜性能方法(IMP),分析了不同褶皱模式对于薄膜振动的影响,分析中还考虑了空气阻尼的影响,并与实验研究结果进行对比分析.Hossai和Jenkins[8-9]研究了具有褶皱的三角形薄膜和环形薄膜的振动特性,褶皱的模拟采用修正材料罚参数方法(PPMM).罚参数是在平面内的小主应力方向上分配一个近似于零的刚度值,以消除刚度矩阵的奇异使计算获得收敛.具有褶皱薄膜的振动模态与不具有褶皱薄膜的振动模态相比发生了很大变化,二者的固有频率也存在着一定区别.
薄膜产生褶皱以后,其平衡位形发生了变化,因此具皱薄膜的振动应当在褶皱的构形基础上进行,才能获得更为精确的分析结果;同时由于褶皱构形引起的薄膜平衡位形的变化及褶皱区域的应力分布特点,导致其振动模态与褶皱构形之间应具有一定的相关性,本方对相关问题进行了分析.
1 具有褶皱薄膜振动的微分方程
薄膜产生褶皱以后,将产生一定的面外变形.具有褶皱的薄膜,将以褶皱构形为平衡位置进行振动.采用拉格朗日方程建立褶皱薄膜振动的微分方程.
振动过程中薄膜弯曲形变势能为

式中:D为弯曲刚度;w为振型函数;v为泊松比.应变势能为
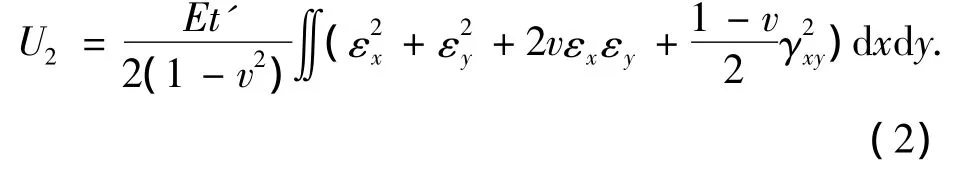
式中:E为弹性模量;t'为薄膜厚度;εx、εy、γxy分别为线应变和剪应变.
只考虑微幅的薄膜面外振动,而不考虑薄膜的面内振动,振动构形函数为w,褶皱的面外变形的表达式为w0,两者均为坐标(x,y)的函数.在这种情况下,应变的表达式为

式(3)代入式(2)得到薄膜应变势能为

设薄膜的密度为ρ,薄膜振动的动能表达式为
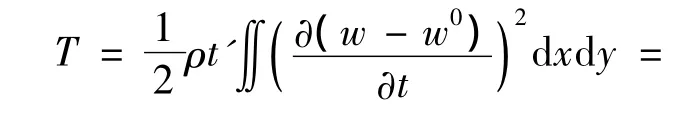
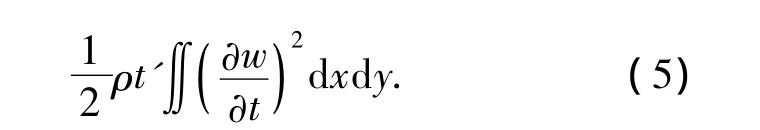
假定振动构形及褶皱构形为如下的级数形式

将式(6)代入式(1)、(4)、(5),得到振动过程势能表达式为

动能表达式为
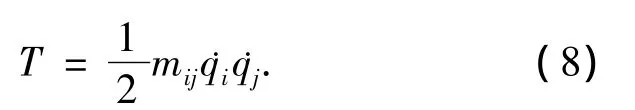

由拉格朗日方程

其中

将式(7)、(8)代入式(14),结合式(13),得

式(15)表示非线性振动的微分方程,如果忽略非线性项的影响,则得到线性振动的微分方程

令qi=aisinωt代入上式有

写成矩阵的形式为

式中刚度矩阵K和质量矩阵M的分量如式(11)和(9)所示,向量A是振动的特征向量,即振动的模态.
由式(11)可知,刚度矩阵中耦合了薄膜平衡位置的褶皱面外变形的影响.由于张力场理论忽略了褶皱引起的面外变形,所以采用基于张力场理论的褶皱薄膜的动态分析,相当于忽略了式(11)中所有与w0有关的项,所以基于张力场理论的动态分析将存在一定的误差.
通过求解方程(18)的特征值和特征向量,可以得到褶皱薄膜振动的固有频率和模态.矩阵的特征值问题可以通过子空间迭代法或兰索斯方法进行求解.
通过有限元方法求解方程(18),其刚度矩阵可由单元刚度矩阵组装而成,即

单元刚阵Ke由3部分组成
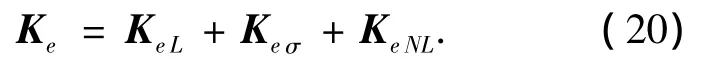
并且

式中:KeL为线性刚阵;Keσ为初应力刚阵;KeNL为大位移刚阵;σ为初始应力;B为应变矩阵;D为弹性矩阵.
通过具有褶皱薄膜的单元刚阵的表达式可以看出,具有褶皱薄膜的动态分析要分两步进行:首先获得薄膜在外载荷作用下的平衡构形,即褶皱构形;然后通过褶皱变形来更新几何模型,从而形成具有褶皱变形影响的刚度矩阵的分量,再通过特征值分析得到系统振动的固有频率和模态.
2 褶皱薄膜振动的数值分析流程
褶皱产生以后,薄膜的构形发生了变化,并且薄膜中的应力分布也发生了变化.所以动态分析应当考虑薄膜构形的变化及其所引起的质量矩阵和刚度矩阵的变化,也就是说,动态分析应当在褶皱构形上进行.为此本文建立了具有褶皱薄膜的动态分析流程如图1所示.

图1 褶皱薄膜动态分析流程
采用壳单元进行薄膜褶皱分析,首先施加小的初始预张力,使薄膜获得一定的初始刚度,便于分析收敛;然后施加微小的面外扰动(通过扰动力的形式来施加)使结构变得不稳定,以便跟踪到分岔路径,获得褶皱构形;施加外载荷进行后屈曲分析(在分析过程中适时的去除外扰动力,以消除扰动对分析结果的影响)获得褶皱构形;通过模型更新来考虑褶皱构形对动态特性的影响,进行考虑有预应力效应的褶皱薄膜的模态分析,得到振动的固有频率和振动模态.
3 算例分析
建立矩形剪切薄膜分析模型如图2所示.薄膜尺寸为380 mm×120 mm,弹性模量、泊松比、密度及薄膜厚度分别为:E=3.53 GPa,v= 0.34,ρ=1 400 kg/m3,t'=50 μm.

图2 剪切矩形薄膜
边界条件为上下边界固定,左右边界自由.上边缘首先向y方向拉伸一个小的距离δ2,以使薄膜中产生一定的初始应力,然后上边缘向x方向产生剪切变形δ1.此时在薄膜中会产生与底边成θ角的斜向褶皱,通过图1流程来分析薄膜产生褶皱以后的动态特性.单元数量为5 080个,初始张拉距离为 δ2=0.1 mm,剪切距离为 δ1= 0~3 mm.分析过程中施加的初始扰动力为0.1 N.
3.1 振动模态与褶皱构形的相关性
当初始张拉距离为0.1 mm,不同剪切距离得到的褶皱变形模式如图3所示.可以看出,随着剪切距离的增加,褶皱的数量并没有发生变化(均为12个褶皱).

图3 不同剪切距离时的褶皱构形
当剪切距离为0.5 mm时,得到具有褶皱薄膜的前四阶模态.图4为褶皱薄膜纵向中线的振动模态与张拉距离为 0.1 mm、剪切距离为0.5 mm时薄膜的纵向中线的褶皱构形的对比.图中实线为振动模态,虚线为褶皱构形.箭头所处的位置为节线位置.从节线的数目来看,随着模态阶数的增加,节线的数目依次减少.通过纵向中线的振型与褶皱构形的对比,可以清晰看出,振动模态与褶皱构形的相关性.由图4可见,对称的振型和反对称的振型交替出现.并且节线的位置都处于褶皱构形的波峰位置.(反对称的振型中,对称轴处的节线除外).以节线为分界,振动模态中存在3种振动形式.Ⅰ型振动:1/2个褶皱波长范围内同向振动,节线的位置为褶皱波峰的位置;Ⅱ型振动:3/4个褶皱波长范围内同向振动,节线的位置为波峰和中面线的位置;Ⅲ型振动:1个褶皱波长范围内同向振动,节线的位置为波峰的位置.依此类推,在更高阶的振型中,将出现3/2个褶皱波长、7/4个褶皱波长、2个褶皱波长等波长范围内的同向振动.3种振型在前八阶模态中的数量分别如表1所示.从3种振型的数量来看,高阶模态的振动形式变得更加复杂,并且有更多的褶皱波峰参与振动.
通过理论分析可知,褶皱波峰处将出现较大的拉应力,并且褶皱的波峰位置在一个褶皱范围内具有最大的面外变形.由此结合式(21)可知,在褶皱的波峰位置将形成较大的局部刚度,这样就导致在褶皱薄膜的振动过程中褶皱波峰多处于节线的位置,不发生振动.并且在高阶模态下,随着褶皱波峰开始参与振动,相应的其振动频率也在增加.由此可见,由于褶皱所形成的面外变形及褶皱区域应力分布的特点,共同决定了褶皱薄膜的振动模态与褶皱构形的相关性.

图4 褶皱薄膜的振动形式与褶皱构形的对比

表1 不同的振动形式分布
3.2 褶皱幅度对振动频率的影响
在薄膜初始张拉距离为0.1 mm时,前四阶固有频率与剪切距离的变化关系如图5所示(上横坐标轴的刻度是与剪切距离对应的褶皱最大面外变形与薄膜厚度的比值).可以看出随着剪切变形的增加,褶皱的变形幅度增大,并且其频率出现了振荡变化.各阶频率与没有发生剪切变形的情况相比明显下降了.
P1~P4(不同剪切距离时对应的基频)点所对应的振动模态如图6所示.图中只显示了节线的位置.由于褶皱的数目没有随着剪切距离的增加而发生变化(均为12个褶皱),所以其节线的数目也没有发生变化,这与前面分析的振动模态与褶皱构形相关性的分析结论相吻合.只是在大的剪切变形的情况下,在薄膜的边缘处出现了局部振动.

图5 剪切变形与振动频率
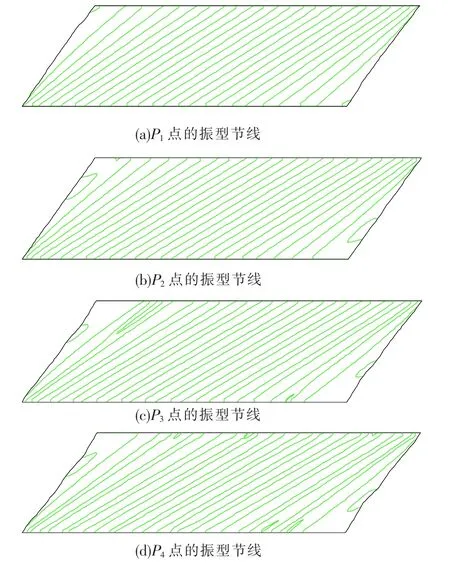
图6 不同剪切距离时的一阶振型
4 结语
首先基于拉格朗日方程建立了考虑褶皱面外变形的薄膜后屈曲振动的微分方程,并基于有限元程序建立了其数值求解过程,基于所建立的求解过程对剪切矩形薄膜的后屈曲动态特性进行了分析.
薄膜后屈曲的振动模态与其褶皱构形具有很大的相关性,振动的节线处于褶皱的波峰位置,随着褶皱的波峰参与振动,其固有频率相应增加,薄膜褶皱的面外变形及褶皱区域的应力分布规律共同决定了这一特点.随着褶皱面外变形幅度的增加,其固有频率发生了振荡变化,与没有发生屈曲薄膜的动态特性相比,产生褶皱以后薄膜振动的固有频率明显减小了.
[1] LI Yunliang,TAN Huifeng,WANG Changguo,et al. Membrane buckling patterns and secondary buckling analysis[J].International Journal of Space Structures,2008,23(3):183-191.
[2] DING Hongli,YANG Bingen.The modeling and numerical analysis of wrinkled membranes[J].Int J Numer Meth Engng,2003,58:1785-1801.
[3] WANG Changguo,LI Yunliang,DU Xingwen,et al. Simulation analysis of vibration characteristics of wrinkled membrane space structure[J].International Journal of Space Structures,2007,22(4):239-246.
[4] RODDEMAN D G,DRUKKER J,OOMENS C W,et al.The wrinkling of thin membranes:part I-theory[J].Journal of Applied Mechanics,1987,54:884-887.
[5] EPSTEIN M,FORCINITO M A.Anisotropic membrane wrinkling:theory and analysis[J].International Journal of Solids and Structures,2001,38:5253-5272.
[6] 李云良,谭惠丰,王晓华.矩形薄膜和充气管的屈曲及后屈曲行为分析[J].航空学报,2008,29(4): 886-892.
[7] KUKATHASAN S,PELLEGRINO S.Nonlinear vibration of wrinkled membranes[C]//44th AIAA/ASME/ ASCE/AHS/ASC Structures,StructuralDynamics,and Materials Conference.Norfolk:[s.n.],2003.
[8] HOSSAIN N M A,JENKINS C H.Wrinkles and gravity effects on transverse vibration of membranes[C]// 46th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics&Materials Conference.Austin,Texas:[s.n.],2005.
[9] HOSSAIN N M A.JENKINS C H.Jenkins.transverse vibration analysis for partly wrinkled wembranes[J]. Journal of Spacecraft and Rockets,2006,43(3):626 -637.

