应用Crystal Ball实现医疗服务系统排队模拟和仿真

厦门大学附属中山医院信息中心(361004) 严 武

排队是日常生活的一个组成部分。就医院而言，在患者的就诊过程中就产生许多的排队现象，如候诊、取药、预约检查等等。许多文献都说明排队时间过长会造成诊疗过程中的一系列问题，陈美珠等〔1〕通过对候诊时间与患者血压、脉搏、状态焦虑(S-AI)的比较，指出候诊时间与患者血压、脉搏、状态焦虑(S-AI)呈正相关。邱访〔2〕和邱静梅等〔3〕通过对门诊患者满意度的调查均发现，患者对候诊时间的满意度较低。陈蓓等〔4〕在其论文中提到患者的排队时间过长也是造成无失医疗纠纷的重要原因。因此，通过对排队问题的研究，找出排队现象的原因和解决办法，对合理配置医疗资源、和谐医患关系等都有十分重要的意义〔5〕。

排队论作为研究排队现象的主要工具，起源于A．K．Ering的著名论文《概率与电话通话理论》〔6〕，后被广泛应用于各个领域，传统的排队论模型往往采用静态的处理办法，即通过确定的达到时间、服务时间等参数，计算出固定的队列长度值，等待时间等指标，而无法实现对整个排队过程的动态模拟，也无法获得如队列长度、等待时间的变化情况和分布情况等更多的动态信息。本文以门诊患者挂号收费排队过程为例，应用排队论结合蒙特卡洛模拟实现对门诊候诊过程的动态仿真，得到多服务台情况下的队列模拟，并对门诊排队现象提出解决相应的建议。

资料与方法

1．资料来源 本文资料来源于厦门市某三甲医院2009年全年工作日门诊患者就诊数据，假定队长为无限，患者按照先到先服务原则进行挂号缴费。患者从等待挂号开始进入排队系统，直到最后离开。

2．方法 应用sql语句对后台his数据库表中的数据进行提取，并将数据转换为Excel文件，用Excel对数据进行筛选清理等预处理，并利用Excel内置函数建立排队系统各个参数间的逻辑关系后，用crystal ball 11.1.1.3仿真软件及VBA编程语言对数据进行

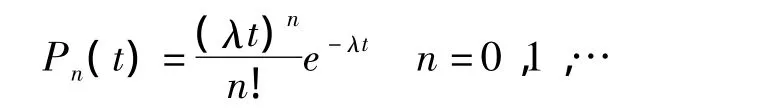
患者到达分布资料经整理后如表1所示，患者的平均到达率λ=26.05(人/分钟)，病人到达的分布服从λ=26.05的泊松分布，即病人到达间隔时间服从1/λ 的负指数分布(χ2=4.8033，df=6，P=0.5693)。M/M/C排队系统的动态仿真。

结果与分析

1．数据模型的拟合

当患者是随机到达时，其间隔时间为负指数分布〔7〕，而患者单位时间的到达分布则应该服从泊松分布。如果在t时段内到达n个患者的概率为Pn(t)，则有:

表1 患者到达的分布拟合

表2为窗口工作人员服务时间的指数分布拟合结果，一共有12个开放窗口，每个窗口现场随机测量20次工作人员的服务时间，假设服务时间服从指数分布，且令服务时间出现在{a，b}(b＞a)时间区间的概率为P(a＜t＜b)，则有:

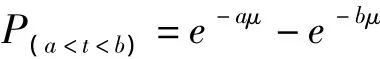
对表2数据的χ2检验表明，工作人员的服务时间服从μ=2.5(人/分钟)的指数分布，结果有统计学意义(χ2=10．1109，df=11，P=0．5204)。

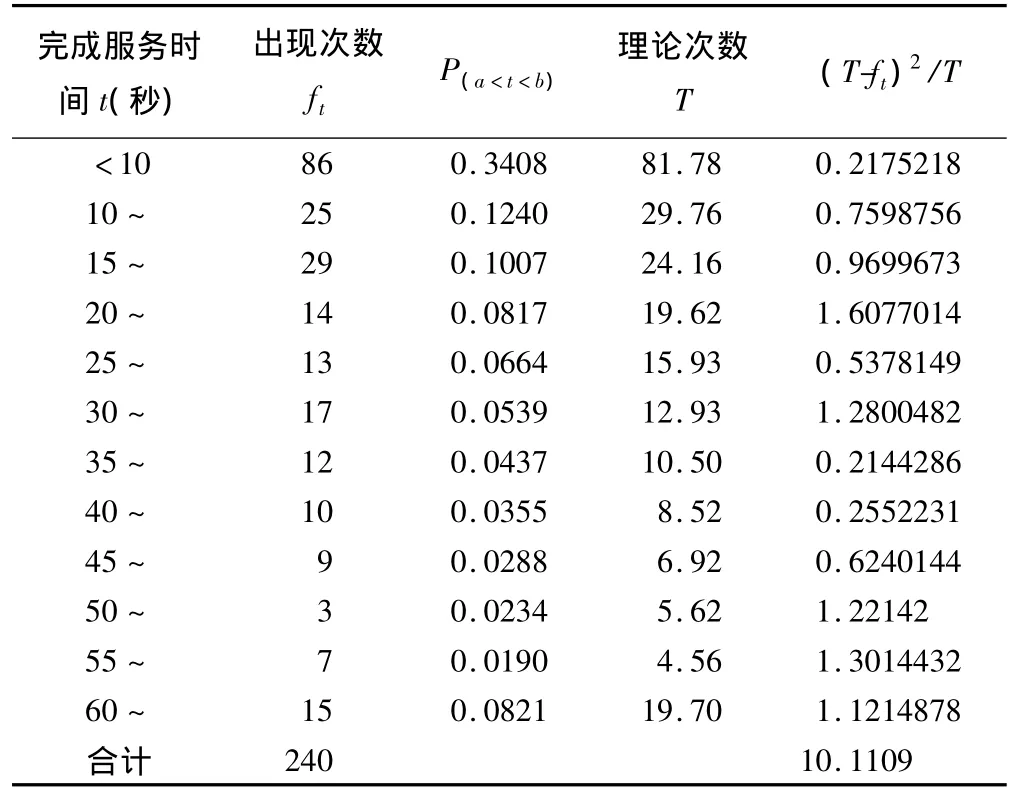
表2 服务时间分布的拟合

2．M/M/C排队系统的的模拟仿真及结果分析Crystal Ball是由美国Decisioneering公司开发的一种运用模拟方法对不确定性(有时也指风险)进行定量分析的软件，后被Oracle公司收购，其应用领域很广泛，使用用户也非常多，据悉在世界500强中有85%的公司，以及美国前50所最佳MBA商学院有40所都在使用它作为解决商业课题和教研的工具〔8〕。国内也有相关的应用和研究，主要集中在商业应用及企业的生产质量控制等领域，在国内医疗卫生行业中的应用却鲜有报道。Crystal Ball作为Excel的一种加载宏运行，在与Excel无缝集成的同时，可以结合Excel的特点，并利用自身模拟的优势，实现对不确定性的定量分析，其基本应用步骤为〔9〕:(1)模型建立。这一步主要是在Excel表中进行，一般根据实际问题情况输入有关数据、公式和设定有关变量，如需要模拟的变量的概率分布(软件中内置的概率分布多达20种，同时也可自己定义分布)、需预测的数据单元;如果是一个决策问题，还需要定义决策变量。(2)模型模拟。当数据输入、模型建立完毕后，点击菜单Run中的Start Simulation(安装启动Crystal Ball后，Excel主菜单中增加Define，Run，Analyze 3个菜单)，便进入模拟运行阶段，由软件自身完成整个模拟过程。(3)结果分析。模拟运行结束后，软件会自动生成有关分析结果，如预测值可以图表形式直观确定对应的概率、预测值的敏感性因素影响分析和运行过程中数据的抽取保存等。

根据对数据的拟合结果，拟采用M/M/C排队模型进行模型仿真，在Excel数据表中分别输入模拟需要的各个参数值，以及需要求解和预测的变量的计算公式。关于M/M/C排队系统的原理、应用条件和计算方法许多教材和论著均有专门的阐述，本文不再列出详细的计算公式。运行crystal ball软件，在单元格中定义λ及μ的分布类型，定义预测变量为队列中的等待人数Lq以及患者在队列中的等待时间Wq，将模拟次数设为5000次，进行蒙特卡洛模拟仿真〔10〕，结果如图1及图2所示。可以看出，而经过5000次 模拟计算出的Lq和Wq的均值分别为3．86人和0．13分钟，排队论公式计算的结果3．5912人和0．1379分钟，差别并不大，如果能适当增加模拟次数，两者的值还会更加接近。则在图1中可以看出，超过3人以上的概率为85．15%，说明队列中排队现象出现的概率还是很大的。另外，结合5000次模拟的Wq频数分布来看，虽然该系统有排队现象，但患者在队列中的等待时间并不长，基本上可以在较短的时间内得到服务。

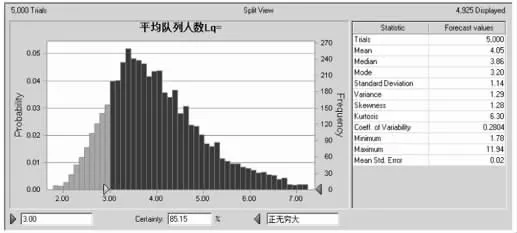
图1 crystal ball中输出的队列等待患者数Lq的模拟结果

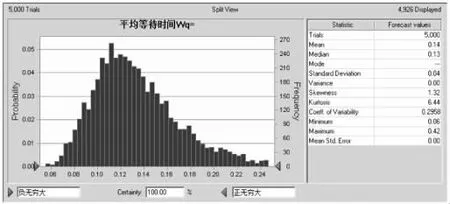
图2 crystal ball中输出的患者在队列中等待时间Wq的模拟结果

我们还可以利用crystal ball中cb．exponential()函数产生随机的指数分布，从而对患者到达的间隔时间和窗口服务时间进行仿真。通过仿真，我们发现，排队的高峰时刻和最大排队人数均出现在9:30～10:00的区间段，这也与我院的实际情况比较吻合。

讨 论

1．到医院就诊排队是一种常见现象，由于患者到达和医疗服务时间的随机性，患者来源数量在理论是无限的，而医疗资源是有限的，当医疗服务的现实需求超过提供该项服务的现有能力时，排队就会发生，因此排队现象是不可避免的。如果患者的等待时间和排队等待的队列长度过长，超过了实际可能承受的限度而远远无法满足患者的需要时，必将造成患者的流失，同时可能影响患者的诊断和救治，使急需诊治的患者无法得到及时的医疗服务，甚至危及患者的生命，影响医疗质量。

2．传统的模拟和预测建模工具往往需要使用者较为专业的理论知识和建模能力，Crystal ball作为一种模拟和预测工具，在应用广泛的Excel电子表格上加载运行，相比其他使用设计复杂的程序和烦琐的计算机编程语言，如 Matlab 6．5、CISMAN、Visual Basic，用Crystal ball建模具有直观简便、操作性更强、适用性更广等优点，降低了建模的难度和操作性，输出的结果清晰易懂，并且可以转换成excel格式文件进行编辑，实现了和OFFICE组件的无缝链接〔11〕。

3．本文以门诊患者就诊流程为例，应用 Crystal ball结合排队论进行M/M/C队列的模拟仿真，在传统排队论的基础上，实现了对排队系统的动态分析，并对仿真结果进行分析和评价，为提高医院的医疗服务效率和优化医疗资源提供了科学参考依据。

1．陈美珠，刘桂卿，冯惠芳，等．候诊时间与状态焦虑的相关性研究．中国行为医学科学，2005，14(9):825-826．

2．邱访．影响我院门诊患者满意度的因素分析及解决方案．华西医学，2009，24(6):1502-1504．

3．邱静梅，王健．山东某县综合性医院门诊患者满意度分析．中国社会医学杂志，2009，26(5):17-319．

4．陈蓓，许翔，江一峰．无过失医疗纠纷的现状分析．中国卫生事业管理，2009，250(4):243-244．

5．周文正，尹平，马玉全，等．排队论模型M/D/c在医疗服务系统中的应用．中国卫生统计，2009，26(6):608-610．

6．Cliff TR．电子表格建模与决策分析．第4版．杜学孔，崔鑫生译．北京:电子工业出版社，2006，530-531．

7．Frederick SH，Mark SH．数据、模型与决策．第2版．任建标译．北京:中国财政经济出版社，2004，593-596．

8．杨琴，胡辉．基于Crystal Ball的项目管理建模分析．中国管理信息化，2007，10(12):27-29．

9．http://download．oracle．com/docs/cd/E12825_01/epm．111/cb_user/frameset．htm?index．html．

10．刘清志，许学娜．Excel在蒙特卡罗模拟分析中的应用．中国管理信息化，2008，11(7):44-47．

11．文伟，叶春明，刘晓乐．基于Excel的蒙特卡罗模拟在银行排队业务中的应用．中国管理信息化，2008，11(6):81-84．