重度增加法与强度折减法的应用对比分析

蔡显杨 许文年 杨学堂 周正军

(三峡大学三峡库区地质灾害教育部重点实验室,湖北宜昌 443002)

有限元强度折减法和重度增加法是求解边坡安全系数和潜在滑动面的两种常用方法.目前,有限元强度折减法已经广泛地应用在边坡稳定分析中,其计算结果稳定可靠,受到广大岩土工程者的青睐.而重度增加法更多的是应用在提防边坡工程中,此类边坡大多由于水位的上升而使得自重荷载增加导致边坡失稳,其在天然边坡和开挖边坡中的应用相对较少,重度增加法在边坡稳定性分析中的适用性和精度仍然在进一步研究中.因此,通过实例分析,对两种方法的计算结果进行了对比分析,并对影响两种方法计算精度的主要因子进行了分析,得出了一些结论.

1 基本原理

1.1 强度折减法基本原理

强度折减法[1]是保持其他因素不变,对影响抗剪强度的粘聚力c和内摩擦角φ同时进行折减,然后将折减后的参数重新输入进行有限元迭代计算,直至边坡处于临界稳定状态,此时的折减系数即为边坡的安全系数.它是从边坡稳定的内因出发,通过不断降低边坡的抗剪强度使边坡过渡到临界状态,其具体表达式为:

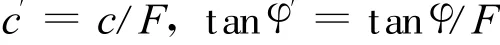
式中,F为边坡安全系数;c、φ为初始粘聚力和内摩擦角;c′、φ′为折减后的粘聚力和内摩擦角.

根据文献[2]的研究,认为有限元强度折减理论和传统的极限平衡法对安全系数的定义是一致的,且采用强度折减法的计算结果与极限平衡法的计算结果相比误差较小,满足工程需求.

1.2 重度增加法基本原理

重度增加法[3]的基本原理和强度折减法的原理正好相反,它是从边坡稳定的外因出发使边坡过渡到极限稳定状态.即保持岩土体的粘聚力c和内摩擦角φ不变,按一定的步数不断增加重力加速度的大小,增加重力加速度就相当于增加了边坡的自重,当边坡达到临界稳定状态时,用此时的重力加速度除以初始的重力加速度即为边坡的安全系数.即:

式中,F为边坡安全系数;glimit为极限稳定状态时的重力加速度;g为初始重力加速度,一般取9.81m/s2.

2 计算失稳的判定标准

目前关于重度增加法和强度折减法计算失稳的判定标准,不同的学者[4-8]有不同的看法,总结起来有如下几种:(1)有限元迭代计算不收敛;(2)塑性应变贯通坡体;(3)坡顶水平位移随着重力加速度增加或强度参数折减时发生突变.

此3种方法在判定边坡是否达到临界稳定状态时各有各的适用性,因边坡的失稳破坏是受各种因素影响的,因此在具体应用时应该综合考虑各种判定标准,而不是单独的去采用某种判定标准.

本文重度增加法采用坡顶水平位移突变和塑性应变贯通坡体的判定标准,而强度折减法采用有限元计算不收敛和塑性应变贯通坡体的判定标准.

3 算例分析

3.1 有限元模型建立及计算过程

根据文献[1]对边坡稳定性进行的研究,最后得出这样的结论:当坡脚到左端边界的距离为坡高的1.5倍,坡顶到右端边界的距离为坡高的2.5倍,且上下边界总高不低于2倍坡高时,计算精度最为理想.因此,选取文献[9]的计算模型,其坡高20 m,坡比1∶1,坡底距左边界的距离为30m,坡顶距右边界的距离为50m,左边界竖直距离为20 m,右边界竖直距离为40m.物理力学参数如下:容重ρ=20kN/m3,粘聚力c=40kPa,内摩擦角φ=20°,弹性模量E=20 MPa,泊松比υ=0.30.

有限元分析时看成平面应变问题处理.采用平面PLANE42四节点实体单元模拟土体,本构关系为理想弹塑性模型.左右边界为法向约束,底部边界为固定端,划分的单元网格如图1所示,单元数为1 019,共1092节点.

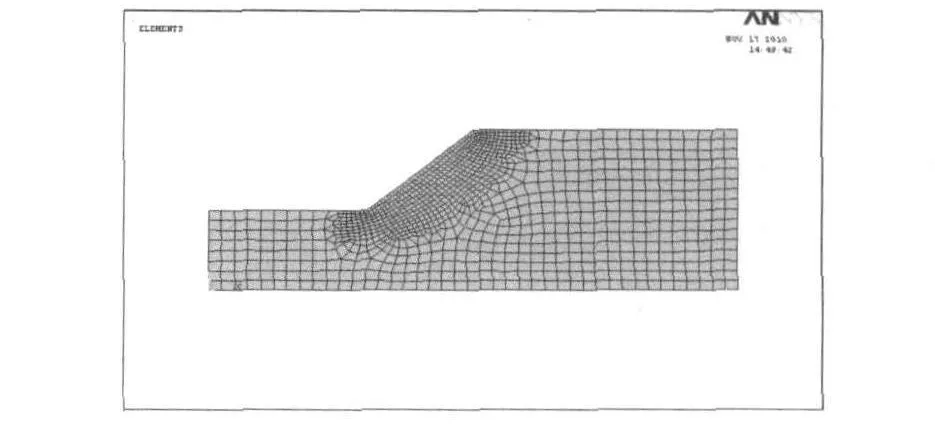
图1 模型网格划分

关于屈服准则的选用[10-11],在许多土力学理论中,如承载力和斜坡稳定性计算,都假设摩尔-库仑屈服准则为常用的破坏准则,但是摩尔-库仑屈服准则在π平面上的屈服轨迹为一不规则的六边形,它在主应力屈服面有一个奇异的顶点,给数值计算带来困难.为了消除角点,德鲁克和普拉格(Drucker-Prager)曾在1952年提出一个内切于摩尔-库仑六棱锥的屈服面,它是一个圆锥面,虽然仍有一个奇异的顶点,但已把原来的拐角消除变成光滑的曲面了.德鲁克和普拉格建议采用的屈服函数为

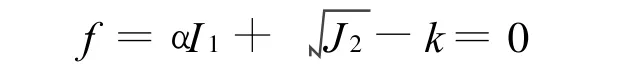
式中,α、k为与岩土内摩擦角和粘聚力有关的参数;I1为应力张量第一不变量;J2为应力偏张量的第二不变量.

其屈服函数形式与广义米泽斯屈服条件是一致的,广义米泽斯屈服准则在π平面上的投影为一个圆.因此,当α、k取不同的值时(具体取值见文献[12]),可用不同半径的圆面代替摩尔-库仑准则不等边的六边形,即代表不同的 Drucker-Prager屈服准则.ANSYS自带的是六边形外角点外接圆Drucker-Prager屈服准则.

根据重度增加法的原理,以1.0,1.1,1.2,1.3, 1.4的规律作为基本步长逐渐增加重力加速度g,当在某一区间坡顶水平位移发生突变时,应该将该区间进一步细分,以找出确切的边坡安全系数.坡顶水平位移随重度增加系数的变化曲线如图2所示(注:图中正值表示与X轴正向相同,负值表示与X轴正向相反).

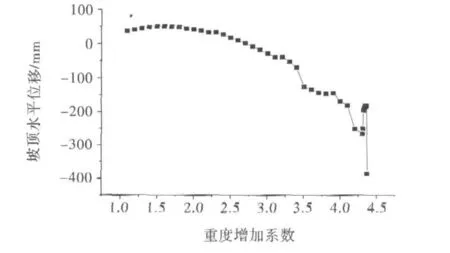
图2 坡顶水平位移随重度增加系数变化曲线

从图2可以看出重度增加系数为1.0～2.7时,坡顶水平位移为正值,且水平位移呈现先增大后减小的趋势;当重度增加系数达到2.8以后,水平位移变为负值且呈现缓慢的增加趋势;当重度增加系数达到4.4时,计算不收敛,边坡可能已破坏.因此,在4.3和4.4之间进一步降低步数,当重度增加系数为4.36时,坡顶水平位移为180.77 mm,当重度增加系数为4.37时坡顶水平位移突然增至384.39 mm,位移发生突变,此时边坡塑性应变场如图3.从图3中可以看出此时边坡的滑面已经相当的明朗且塑性应变区贯通整个坡体,则可认为边坡已达到临界稳定状态.因此,采用重度增加法所得的边坡稳定系数为4.37.

3.2 两种方法计算结果对比分析

采用强度折减法计算该边坡,当折减系数达到1.70时,有限元计算不收敛,且由图4可以看出此时塑性应变贯通坡体,可认为边坡已达临界稳定状态.所以可认为采用强度折减法所得边坡安全系数为1.70.

将两种方法计算所得到边坡安全系数系数按不同的Drucker-Prager屈服准则转化(不同屈服准则安全系数转化方法见文献[13]),并与极限平衡Janbu法所计算的结果进行比较,见表1.

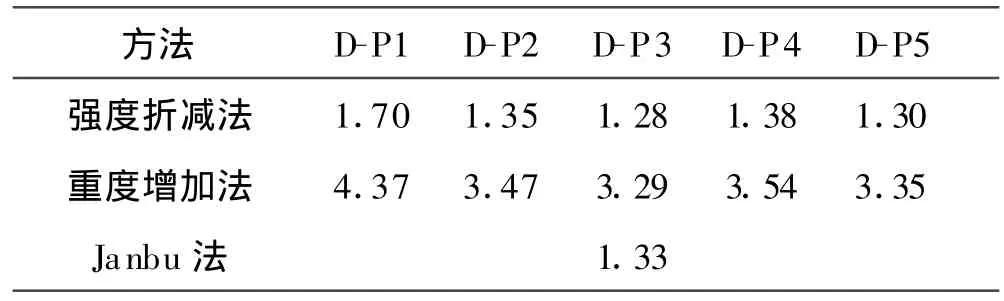
表1 计算结果对比

从表1中可以看出:(1)采用相同的D-P屈服准则时,重度增加法的计算结果比强度折减法计算的结果普遍偏大;(2)当强度折减法采用适当的屈服准则时能很好的与极限平衡法计算结果相吻合,其最小误差在1.5%,可以认为强度折减法在计算边坡安全系数上是可靠的;(3)重度增加法与极限平衡法的计算结果相比,无论采用何种屈服准则所计算的结果均比极限平衡法计算的结果要偏大,由此可见重度增加法的计算精度还需进一步讨论.

4 影响计算精度参数分析

由文献[14]知,弹性模量E、泊松比υ、剪胀角 ψ对边坡稳定计算精度影响较小,故本文选取粘聚力c,内摩擦角 φ,坡角α 3个参数讨论其对重度增加法和强度折减法计算精度的影响.计算结果如图5～7所示.

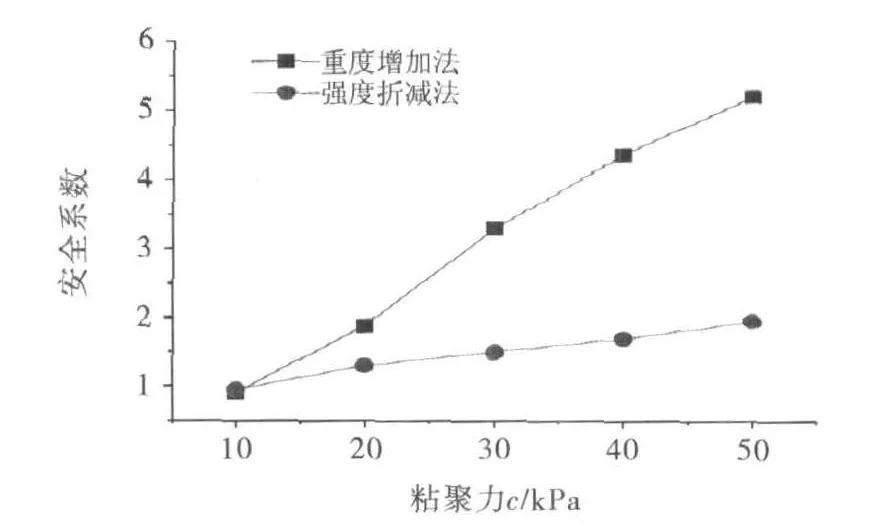
图5 粘聚力对计算精度的影响

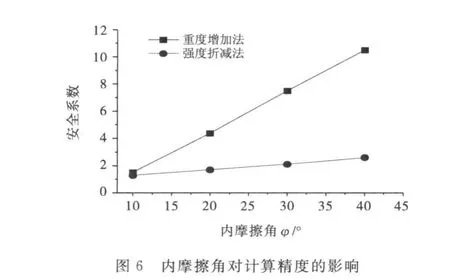
从图中可以看出粘聚力c、内摩擦角φ、坡角α对重度增加法计算结果影响非常显著,而对强度折减法计算结果影响则较为平缓,故采用强度折减法的计算结果可靠而采用重度增加法的计算结果不太理想.另外,在粘聚力和内摩擦角较小而坡角较大时,采用重度增加法和强度折减法的计算结果比较接近,可以认为在坡度较陡而抗剪强度参数较小时采用重度增加法的计算结果是比较可靠的,而对坡度较缓且抗剪强度参数较大时,其计算精度因受到因素影响较大而使其计算结果与强度折减法的计算结果相比误差较大.其原因主要是当增加重力加速度时,坡体的自重增加,则下滑力也增加,但是在下滑力增大的同时,其抗滑力也同时在增大,当抗剪强度参数较小且坡度较缓时,根据抗剪强度公式可知抗滑力的增加幅度可能比下滑力的增加幅度要大,从而使得所计算边坡的安全系数增大而影响计算精度.

5 结 论

(1)当采用适当的屈服准则时,强度折减法计算的边坡安全系数与极限平衡法计算的结果较为吻合,满足精度要求.

(2)无论采用何种屈服准则,重度增加法计算的边坡安全系数普遍较极限平衡法和强度折减法的计算结果偏高.

(3)通过对影响计算精度的3因数(粘聚力c、内摩擦角φ及坡角α)进行分析,结果表明此3因素对强度折减法的计算结果影响较为平缓,而对重度增加法计算结果影响非常显著.

(4)只有在在抗剪强度参数较小而坡度较陡的情况下,重度增加法的计算结果才较为可靠.

[1] 郑 颖,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57-78.

[2] 赵尚毅,郑颖人,时卫民,等.用有限强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.

[3] 康亚明,杨明成,胡艳香,等.基于重度增加法的边坡稳定性三维有限元分析[J].建筑科学与工程学报,2006, 23(4):49-53.

[4] 郑颖人,赵尚毅,邓卫东.岩质边坡破坏机制有限元数值模拟分析[J].岩石力学与工程学报,2003,22(12):1943-1952.

[5] 张鲁渝,郑颖人,赵尚毅.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003,(1): 21-27.

[6] 郑 宏,李春光,李焯芬,等.求解安全系数的有限元法[J].岩土工程学报,2002,24(5):626-628.

[7] 刘军王,正 中,牟声远.有限元重力加大法计算边坡安全系数[J].路基工程,2008,(5):130-131.

[8] 张文卫,赵蒙生.重度增加法在边坡稳定性上的应用[J].西部探矿工程,2009,(5):1-3.

[9] 康亚明,刘长武,贾 延,等.重度增加法确定边坡潜在滑动面[J].人民长江,2008,39(8):75-77.

[10]时为民,郑颖人.摩尔-库仑屈服准则的等效变换及其在边坡分析中的应用[J].岩土工程学报,2003,1(3):155-159.

[11]陈远川.有限元强度折减法计算土坡安全系数的研究[D].重庆:重庆交通大学,2009.

[12]柳林超,梁 波,刁 吉.基于ANSYS的有限元强度折减法求边坡安全系数[J].重庆交通大学学报,2009,28 (5):900-901.

[13]赵尚毅,郑颖人,刘明维,等.基于Drucker-prager准则的边坡安全系数定义及其转换[J].岩石力学与工程学报, 2006,25(1):2730-2734.

[14]徐卫亚,肖 武.基于强度折减和重度增加的边坡破坏判定标准[J].岩土力学,2007,28(3):505-510.