考虑混凝土抗拉的开裂截面墩柱的中性轴位置研究

彭建中 郑 罡

(1.重庆交通大学土木建筑学院,重庆 400074;2.招商局重庆交通科研设计院有限公司,重庆 400067)

自1971年美国San-Fernando地震爆发后,延性抗震设计理念越来越受到工程界的重视,延性抗震设计方法已被许多桥梁抗震规范采纳.1998年颁布的欧洲规范8第二部分结构抗震设计(EUROCODE 8, Design of structures for earthqua-ke resistance-Part II,Bridges)[1]、2006年6月颁布的美国加州运输部抗震设计标准v1.4版(CALTRANS Seismic Design Criteria,Version 1.4)[2]、2002年日本道路协会颁布的《道路桥示方书◦同解书V抗震设计篇》[3]以及2008年我国交通运输部颁布的《公路桥梁抗震设计细则》(JTG/T B02-01-2008)[4]等桥梁抗震规范都是采用基于延性的抗震设计方法.在基于延性的设计理论中,主要有曲率延性系数与位移延性系数两种指标,其中,刚度作为影响延性的重要部分之一,它的取值对桥梁延性抗震设计有着极其重要的作用.

在开裂刚度的计算过程中,首先要考虑中性轴的位置.以往对墩柱中性轴位置计算公式的推导,大都忽略了混凝土抗拉强度的影响,本文在考虑混凝土抗拉强度条件下,对墩柱开裂后中性轴位置进行求解.

1 基本假设及研究对象

(1)平截面假定:受弯之前的正截面在受弯后仍保持平面,截面应变保持平面分布,同时忽略剪切变形和滑移变形,只考虑弯曲变形的影响.(2)弹性体假定,在弹性范围内,钢筋与混凝土的应力-应变关系均为理想的线弹性.(3)对称配筋假设:钢筋混凝土截面配筋是对称的.

对于一般的钢筋混凝土矩形桥墩,在地震力作用下,其受力形式可以简化为构件在墩顶截面受轴向压力与水平集中力的共同作用的形式,如图1所示.

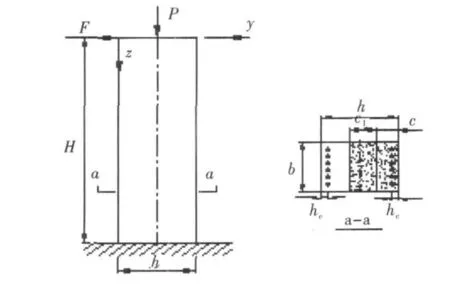
图1 钢筋混凝土墩柱截面及受力简图

图中截面宽度与高度分别为b、h;钢筋中心混凝土保护层厚度为 hc;截面中所配钢筋的总面积为As0;c为截面中性轴至受压区边缘的距离,即混凝土受压区高度;c1为截面中性轴至受拉区混凝土开裂边缘的距离;H为墩柱有效高度.

2 变换截面法及平衡方程的建立

图2 钢筋混凝土构件变换截面示意图

图3是通过变化截面后的示意图,As=αEAs0为与混凝土弹性模量相同的钢筋面积,As0为钢筋计算面积.

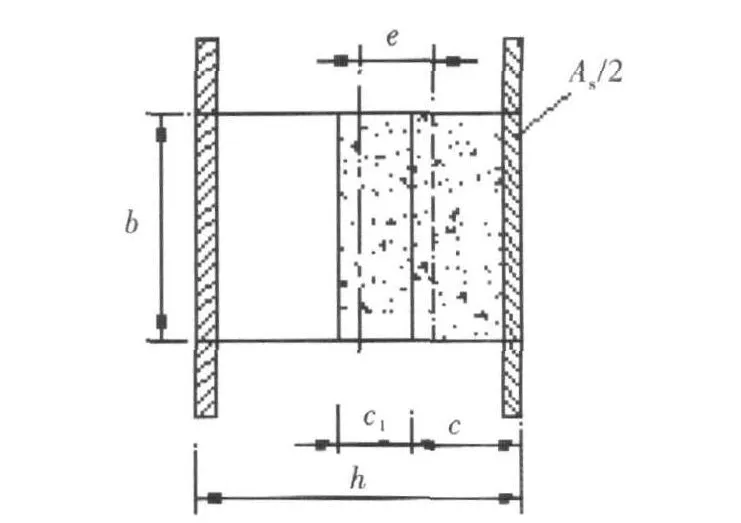
图3 墩柱构件开裂截面简化图

根据基本假设,所示的墩柱构件中的任意开裂截面,截面的应力-应变关系如图4所示.

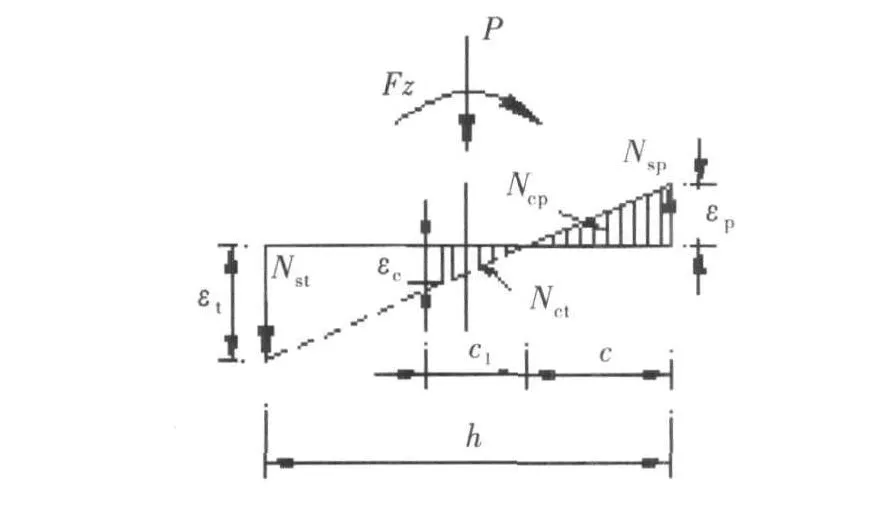
图4 开裂截面的应力-应变关系图

e为截面开裂前、后形心轴移动的距离,其大小可根据形心轴两侧的面积矩相等确定:

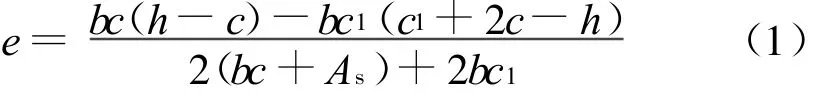
由相似三角形关系可以得到开裂截面的应变协调方程:

图3所示的开裂截面,受拉钢筋的拉力Nst、受压钢筋的压力Nsp、受拉区混凝土的拉力 Nct以及受压区混凝土的压力Ncp分别为:

墩柱在墩顶水平力和轴压力两个外力作用下,可建立如下力平衡方程与力矩平衡方程:

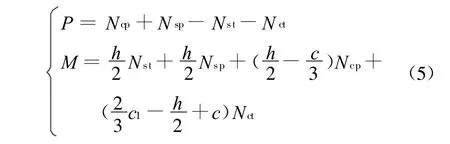
将式(2)、(3)、(4)代入式(5)中可得任意开裂截面中性轴至受压区混凝土边缘的距离c关于相应截面到墩顶截面的距离z的函数.

其中:

式(6)表明,c的解析解很难解出,但在弹性范围内,对于材料、截面与受力特征明确的矩形双筋混凝土墩柱构件,构件的任意开裂截面的中性轴位置是确定的.

3 计算实例

某墩柱不考虑混凝土保护层厚度对计算结果的影响.截面高度hh为27cm,截面宽度b为45cm,钢筋重心保护层厚度hc=2.5 cm,墩高H为1.8 m,设计轴压比μ为0.1,构件采用C30混凝土和HRB335钢筋,墩柱纵筋率ρ为1.27%,配箍率为0.7%,纵向钢筋采用 Φ 14带肋钢筋,箍筋为 Φ 8光圆钢筋.为便于分析计算,本文假设墩底首次屈服发生于墩底受拉钢筋,认为屈服应变ε为0.002,混凝土拉坏应变为εc=0.000046.

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ D62-2004),查出C30混凝土抗压强度设计值为fc=13.8MPa,弹性模量Ec=30 000MPa; HRB335钢筋的弹性模量Es=200000MPa,根据轴压比定义,求解轴向压力P=μ fcbh=167.67kN,根据纵筋率定义,求解与混凝土弹模相同的纵筋换算面积As=ρ bhEs/Ec=0.0103m2.在不考虑混凝土抗拉力时,墩底首次屈服时墩底所能承受的最大弯矩值Mmax=78.746 kN◦m和最大水平力Fmax=43.748 kN.当c=h时,截面为全截面受压,此时z=16.69 cm,混凝土临界开裂位置z=30.42 cm,此时c= 16.79cm.

在z为16.69cm至30.42 cm之间,由于受拉混凝土未屈服,抗拉应变为未知量,本文推荐用混凝土抗拉应变插值法(0,εc)求此处的受压区高度c,本例结果如图5～6所示.

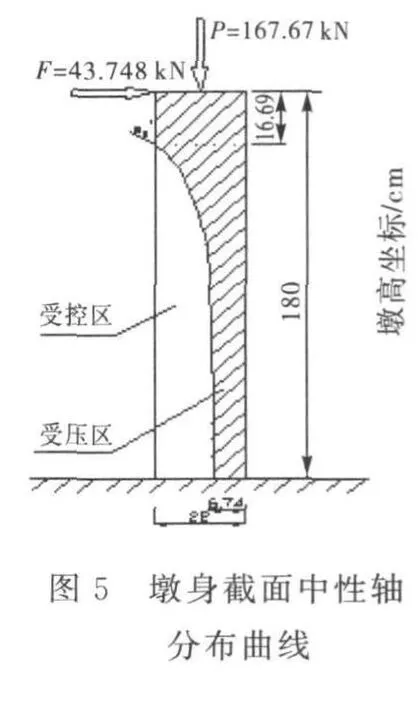
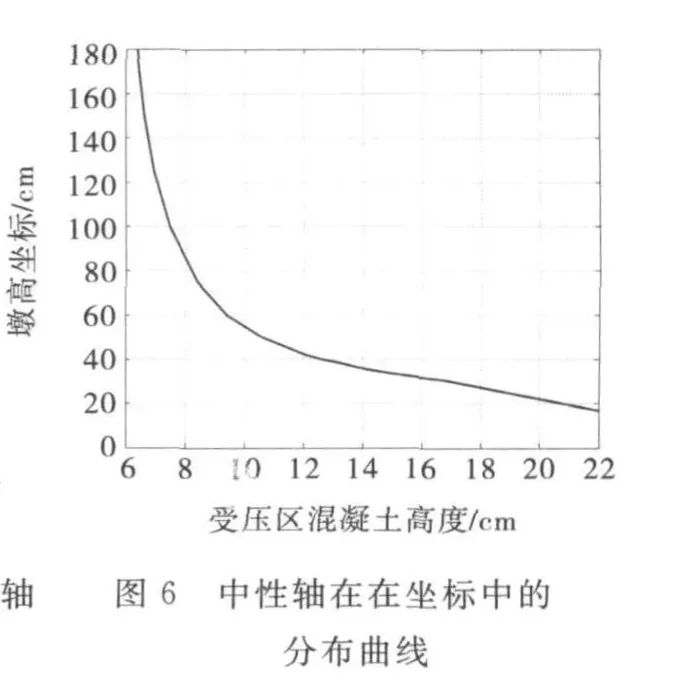
4 结 语

本文在考虑混凝土抗拉强度情况下进行了墩柱截面中性轴的位置公式推导.建议在全截面受压区墩身高度至墩柱截面混凝土开裂临界点墩身高度处混凝土拉应变值用插值法求得.本文推导的钢筋混凝土桥墩开裂截面中性轴的计算公式只是针对双筋矩形截面的墩柱,并不适用于四面布筋和圆形截面的墩柱整体刚度计算,需要今后进一步分析推导.墩柱中性轴位置计算公式可运用于钢筋混凝土悬臂桥墩变形分析,对后期截面刚度的计算以及墩柱混凝土开裂前沿的求解有一定的参考意义.

[1] CEN.Eurcode8-Design Provisions for Earthquake Resistance of Structures,Part2:Bridges[M].Committee European De Normalization(CEN),1998.

[2] CaliforniaDepartmentofTransportation(CALT RANS).Seismic Design Criteria,Version1.4[S].California,2006.

[3] 日本道路协会.道路桥示方书◦同解说.V耐震设计篇[M].东京,平成14年3月.

[4] 重庆交通科研设计院.JTG/T B02-01-2008.公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.

[5] 帕克 R,波利 T.钢筋混凝土结构[M].秦文钺,译.重庆:重庆大学出版社,1986.

[6] 铁摩辛柯 S P,格尔 J M.材料力学[M].李春亮,译.2版.台北:晓园出版社,1985.