从空间到 QK(p,q)空间上的Volterra型复合算子
张铮,谭海鸥
(五邑大学 数学与计算科学学院,广东 江门 529020)
张铮,谭海鸥
(五邑大学 数学与计算科学学院,广东 江门 529020)
记D是复平面的开单位圆盘,H( D)表示D上的解析函数的全体,给出并证明了从空间到 QK(p,q)空间上的Volterra型复合算子有界性和紧性的充分必要条件.
Volterra型复合算子; QK(p,q)空间;空间;有界性;紧性
1 引言及预备知识
设 φ∈ B( D),y( z)∈ H( D ),算子Iy,φ定义为称为Volterra型复合算子.
定义1[1]设分别为加权空间、加权小空间.
定义2[2]设且满足

称 f属于 QK(p,q)空间.其中权函数K满足以下条件:
a)K为非减函数;
b)K在(0,1)上二阶可微;

关于Volterra算子Jφ已有很多研究成果,如于燕燕[2]刻画了Bloch空间上的型复合算子有界性的充分必要条件;黄小玲等[3]刻画了Bloch型空间中B Bα→ Volterra算子的有界性;瞿丹[4]讨论了Bloch型空间中的Volterra算子的有界性.本文给出并证明了从加权Bloch型空间到 QK(p,q)空间上的Volterra型复合算子有界性和紧性的充分必要条件,其中C表示常数,在不同的地方C表示不同的值.
2 预备引理
引理1[5]存在函数使得
3 主要结果
定理1 设α>0,0<p<∞,q>-2,φ是D→D一个全纯自映射,则以下结论等价:

证明 3)⇒1).设结论3)成立并且 C( C > 0)是结论3)的上确界,如果则由闭图像定理只需证 Iy,φ( f)∈ QK(p,q).由结论3)有


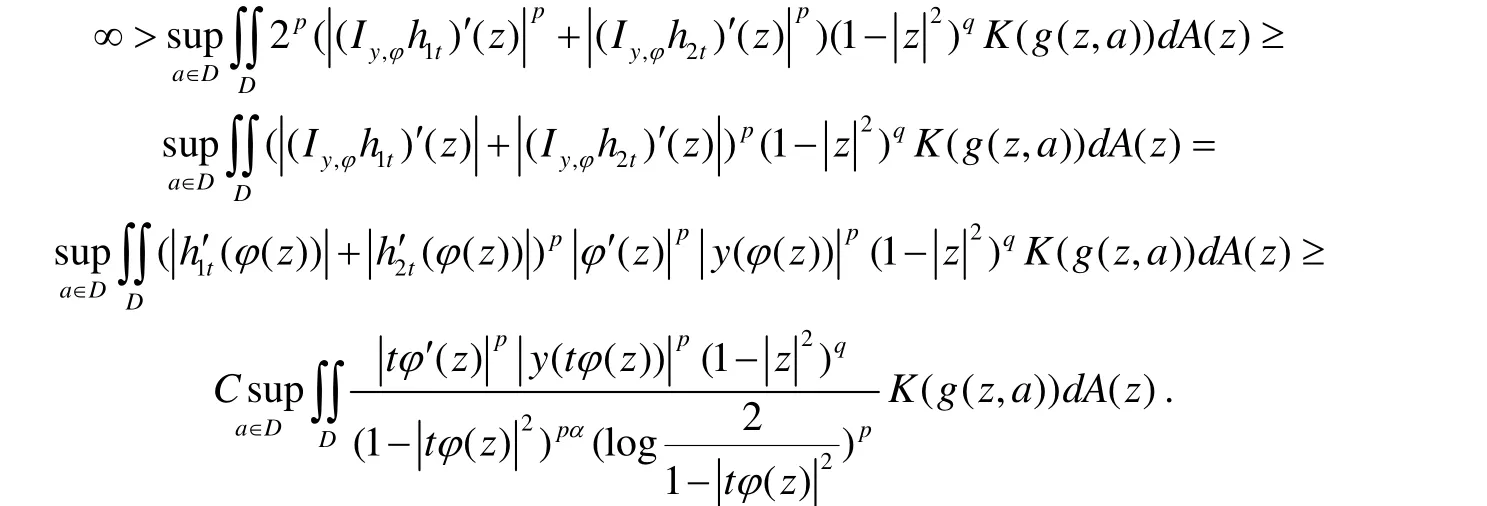
定理2 设α>0,0<p<∞,q>-2, K :[0,∞) → [0,∞)为非减函数,且 φ∈ B( D),则下列结论等价:
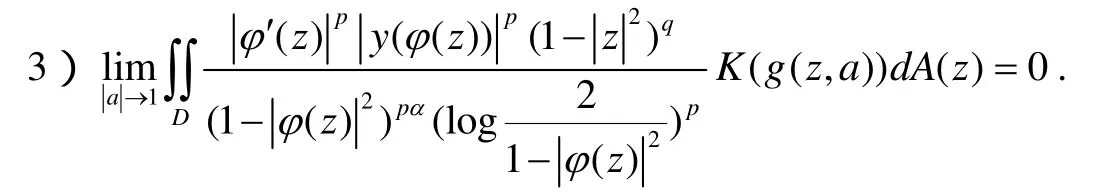

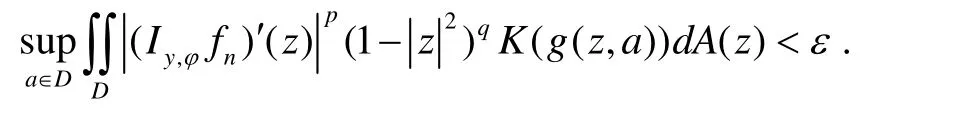
由结论3),存在 δ: 0 <δ<1,使得
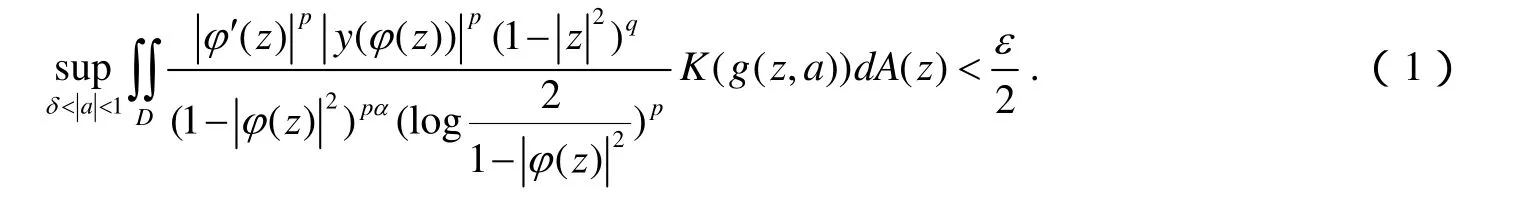
设a∈D,0<t<1,记Dt={z∈ D:z>t},令
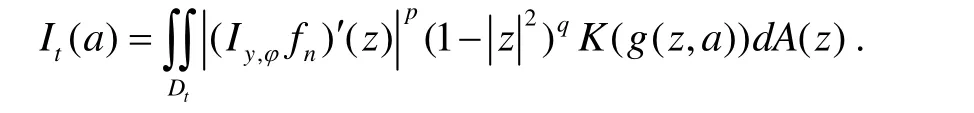
因 Iy,φ(fn)∈ QK(p,q),0,故则∀a∈D,存在ta,0 < ta<1使 Ita(a)<ε.由于 It( a)是关于a的一个连续函数,故存在a的领域N( a)⊂D,使得 Ita(z)<ε(z ∈N( a )).因且为闭集,故存在 N( a1),… ,N( am),使得对 ai( i = 1,2,… ,m)存在tai,使得 Itai(z) <ε(z ∈ N( ai),i =1,2,…,m).令 t0= max{ta1,… ,tam},则当a≤δ时, It0(a)<ε,所以




2)⇒1)显然成立.

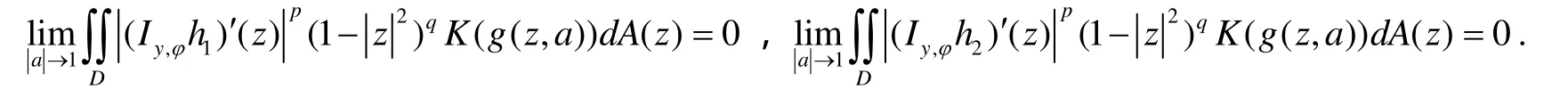
所以,
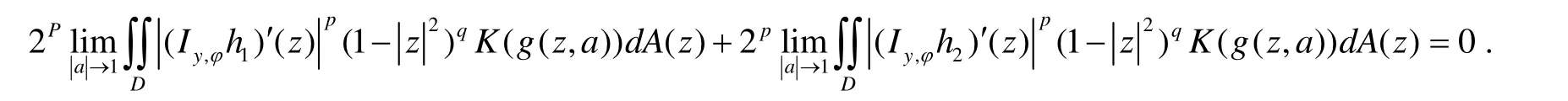
故结论3)成立.
[1]谭海鸥.一类加权 α- Bloch 空间上复合算子的有界性和紧性[J].五邑大学学报:自然科学版,2004,18(4): 7-10.
[2]于燕燕.Volterra-type composition operators from logarithmic Bloch spaces into Bloch-type spaces[J].徐州师范大学学报:自然科学版,2009,27(3):14-18.
[3]黄小玲,叶国栋.Bloch型空间上的广义 Volterra型算子的有界性[J].数学的实践与认识,2009,39(12): 205-208.
[4]瞿丹.Bloch型空间上的Vloterra算子[J].韩山师范学院学报,2008,29(3):9-11.
[5]LI Haiying,LIU Peide.Composition operators between generally weighted Bloch spaces andspaces[J]. Banach J of Math Anal,2009,3(1):99-110.
Volterra-type Composition Operators fromSpaces to QK(p,q)Spaces
ZHANG Zheng,TAN Hai-ou
(School of Mathematics and Computational Science,Wuyi University,Jiangmen 529020,China)
LetDbe a unit disk of the complex plane,H( D)be the sum of analytic functions in the open unit disk.The boundeness and the compactness of the Volterra-type composition operators from weighted Bloch-type spaces to QK(p,q)spaces are proved.
Volterra-type composition operators; QK(p,q)spaces;spaces;boundeness;compactness
O174.5
A
1006-7302(2011)03-0007-05
2011-01-05
张铮(1984—),女,湖北襄阳人,硕士研究生,研究方向为复分析及其应用;谭海鸥,教授,硕士生导师,通信作者,主要从事复分析方面的研究.

