复杂网络社区挖掘——改进的层次聚类算法
郑浩原,黄 战
(暨南大学 信息科学技术学院 计算机科学系,广东 广州 510632)
复杂网络表示现实世界中具有网络结构特性的诸多系统,它通常具有显著的社区结构,同质顶点聚集在同一社区,异质顶点分布于不同社区,表现为社区内部顶点之间连接边稠密,社区之间连接边数量相对稀疏[1]。社区挖掘是复杂网络分析领域的热点问题,可以将现有的社区挖掘算法归纳为三大类[2]:基于优化的算法、启发式算法以及其他算法。基于相似度的层次聚类算法[3]属于其他算法,这类算法不需要任何先验知识就可以有效地发现复杂网络中的社区结构。当前的层次聚类算法的主要缺点是需要计算所有顶点对之间的相似度,时间复杂度为O(n2),n表示图中顶点数量,不适用于大规模网络分析。针对这一缺点,受到社交网络分析相关方法的启发,本文提出一种改进的层次聚类算法。
社交网络分析[4]是复杂网络分析的一个分支,社交网络中有一类Ego Networks,表现为有一个中心结点(即ego),图中所有其他结点(称为alters)与中心结点直接连接,alter之间也有边相连。社会学理论[5]指出,关系紧密的角色之间相似度偏高,如果两个角色之间共同点越多,则这两者就越有可能是朋友或者具有紧密的联系。当与某确定角色比较,角色A与角色B的相似度值接近时,可以认为角色A与B具有某种同质性。基于这一理论,对层次聚类算法进行改进,在探测出网络中扮演ego角色顶点的前提下,计算其他顶点与ego的相似度,而不是计算所有顶点对之间的相似度,此种情况下,算法时间复杂度为O(n),计算负荷与网络规模呈线性相关。实验结果表明,该算法可能在准确性上稍有不足,但是能有效降低网络分析规模、计算复杂度和大致发现网络中的社区结构。
1 算法准备
1.1 相似度计算
相似度[3-4]是对图中顶点之间的相似或者相异程度的度量,是层次聚类算法的核心概念,可以大致将现有的相似度计算方法分为三大类:
第一类,可以将顶点嵌入到n维欧式空间中,通过给顶点分配合理的n维坐标,将网络聚类问题转化为空间点聚类问题。给定两个顶点,A=(a1,a2,…,an)和 B=(b1,b2,…,bn),则可以利用各种距离度量方法计算两者的距离。例如,欧几里得距离:
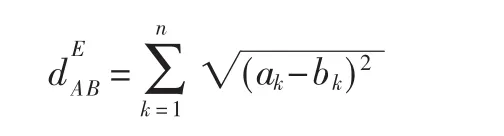
第二类,如果顶点不能嵌入到欧式空间中,这种情形下,还可以根据图中顶点之间的邻接关系计算相似度。一种方法将顶点间距离定义为:
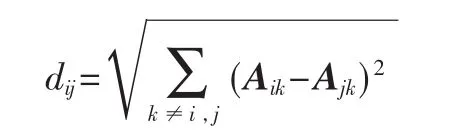
A表示图的邻接矩阵。这是一种基于结构同等概念的度量顶点相异度的方法。结构同等指两个顶点之间有相同的邻接顶点,若 i和 j结构同等,则 dij=0;顶点度高且存在较多不同邻接顶点的顶点之间,相异度高。
根据图的邻接矩阵,可以利用行或列向量表示顶点之间的海明距离度量顶点间的匹配程度,也是相似度度量方法之一。例如,有如下邻接矩阵A:

顶点 A=(0,1,1,1)、B=(1,0,0,1),则两者之间的海明距离是3,表示了两者对应位置不同位的个数。其他度量顶点间匹配程度的方法还包括计算顶点间的杰卡德系数等。
第三类,根据图本身的构造和属性特征设计的一些方法。例如,一种度量相似度的方法是利用两个顶点间独立于边(或顶点)的路径的数量。独立路径之间不共有任何边(或顶点)。根据最大流/最小截理论,每条边只能承载一个流单元,则独立路径数量等于两个顶点间能够传递的最大流。据此设计的算法(如增广路径算法)能够在O(m)时间复杂度下计算最大流,m表示图中边的数量。
1.2 Ego角色的探测
复杂网络分析中,中心度[6]是顶点在图中重要性的度量,“重要”的具体含义要视具体情况而定,例如社交网络中的中心人物角色。本文引入EgoNetworks中的概念,将重要顶点命名为ego。目前有四种中心度度量方法被广泛使用。
(1)Degree Centrality,顶点的度指图中与顶点相关联的边的数量(本文只讨论无向图)。用数学形式表示为,图 G的邻接矩阵 A,若 Aij=1,则存在连接 i和 j的边;若Aij=0,则 i和 j无连接。 顶点数为 n时,顶点 i的度 ki:
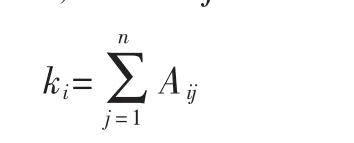
虽然形式简单,顶点的度经常能有效地衡量顶点的重要性或影响力:在社交网络中,拥有更多连接边的角色往往更具影响力。
(2)Eigenvector Centrality,这种中心度量方法的基本思想是:给图中所有顶点赋予相应的分值。赋分原则是:考虑某一顶点v,v的所有连接边中,来自高分顶点的连接较来自低分顶点的连接给贡献更多的分值。谷歌的PageRank算法即是这种度量方法的一个变种。
利用图的邻接矩阵计算Eigenvector Centrality:xi表示第i个顶点的分值,则xi与i的所有邻接顶点的分值的和成正比:
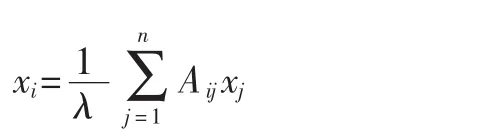
上式中λ是常量。定义中心度的向量形式x=(x1,x2,…),可以重写上式为:
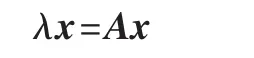
可见,x是邻接矩阵A的特征向量,对应的特征值是λ。一个特征向量往往对应多个特征值,假设中心度值非负,根据Perron-Frobenius定量,λ则取所有特征值中最大的值,对应的特征向量为x。
(3)Betweenness Centrality,图中那些位于更多的顶点对之间最短路径上的顶点拥有更高的介度。顶点v的介度CB(v):
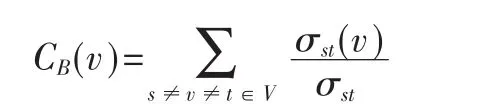
σst表示 s与 t之间最短路径的总数,σst(v)则是这些最短路径中经过顶点v的最短路径数量。
(4)Closeness Centrality,定义为顶点v与图中所有其他可达顶点之间的最短路径的均值,表示为:
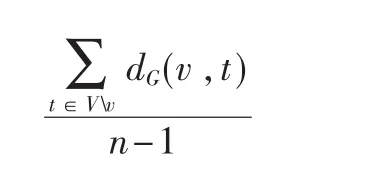
其中n≥2表示由v起始可以到达的网络中的连接组件V的大小。亲近度可以衡量图中信息由给定的顶点传播到其他可达顶点所需时间的长短。
1.3 模块性标准
模块性标准[7]由Newman等人引进,用以衡量算法发现的社区结构质量。复杂网络G=(V,E),其中,V为顶点集合,E为边集合,G包含了n个顶点,k个社区,定义模块性:
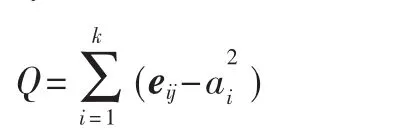
式中,e是一个k×k维的对称矩阵,eij表示连接社区 i中角色(即顶点)和社区j中角色的边的数量在边总数中所占比例,表示与第i个社区中角色连接的边在边总数中所占比例。Q值介于0~1之间,Q值越接近1,说明发现的社区结构质量越高。实际网络中,Q值一般在0.3~0.7之间。
2 改进的层次聚类算法
用于表示现实网络系统的复杂网络通常具有的层次结构特征,即较大的社区结构包含较小的社区结构。层次聚类算法能有效地发现这种层次结构,被广泛应用于社交网络分析、生物工程、市场分析等领域。层次聚类算法可以分为两大类:
(1)凝聚方法:采用自底向上的策略,首先将每个对象作为簇(cluster),然后合并这些原子簇成为更大的簇,直到所有对象都在一个簇中,或者满足某终止条件。
(2)分裂方法:采用自顶向下的策略,首先将所有对象置于一个簇中,然后逐步细分为越来越小的簇,直到每个对象各为一簇,或满足某终止条件,例如达到了希望的簇数或每个簇的直径都在某个阈值内。
由于分裂方法很少使用,本文讨论的算法采用自底向上的策略。通常可以用树状图(dendrogram)表示层次聚类的过程,如图1所示。
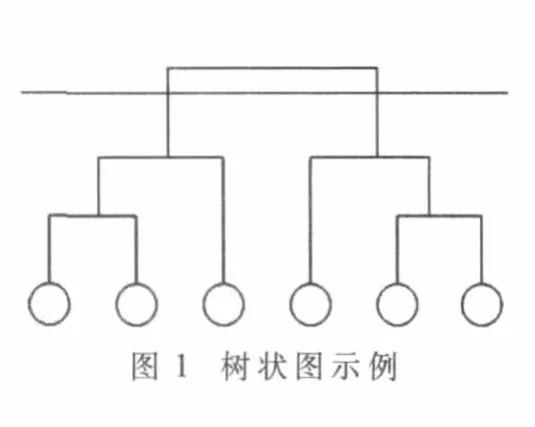
层次聚类算法将网络划分为几个社区取决于在什么位置分割树状图,如图1中横线位置将产生两个社区结构。实际网络中通常依据模块性标准来确定最佳的划分位置。
传统层次聚类算法在确定相似度计算方法后,计算所有顶点对之间的相似度。本文在传统方法的基础上,引入ego角色探测过程,根据复杂网络具体特征,首先确定相似度计算方法,然后确定ego角色的探测方法,一旦扮演ego角色的顶点被确定,则只计算图中所有其他顶点与ego顶点之间的相似度,这种情况下,时间复杂度取决于ego探测过程,例如,选定Degree Centrality作为ego探测策略,总的时间复杂度可表示为O(n)。可见,在大规模网络分析中,改进的层次聚类算法具有较大优势。算法步骤如下。


该算法可以有两种应用用途:在较理想的情形下,例如复杂网络表示的是现实的EgoNetworks,则算法能有效挖掘网络中的社区结构;对于准确度要求很高以及复杂网络规模巨大、特征不明确的情形,本文算法可作为网络预处理过程,用于降低网络分析规模,此时算法只产生规模合适的粗糙的社区,再运用其他准确度较高的算法,划分出更精确的社区。
3 实验分析
3.1 EgoNetworks中的算法应用
该EgoNetworks数据采集自社交网站人人网,包含了一个Ego角色和49个alter角色。图中顶点代表一个个体,边表示个体之间的好友关系。由调查得知,该网络包含三个同学群体,一个陌生人群体,一个亲密好友群体。运用改进的层次聚类算法,成功地挖掘出了网络中包含的五个社区,算法采用的相似度计算方法是顶点间海明距离,ego角色在初始状态是已知的,第一次迭代后利用Degree Centrality探测新的ego角色。图2描述了模块度Q值随社区个数变化的分布图,x轴表示社区数量,y轴表示对应的Q值。
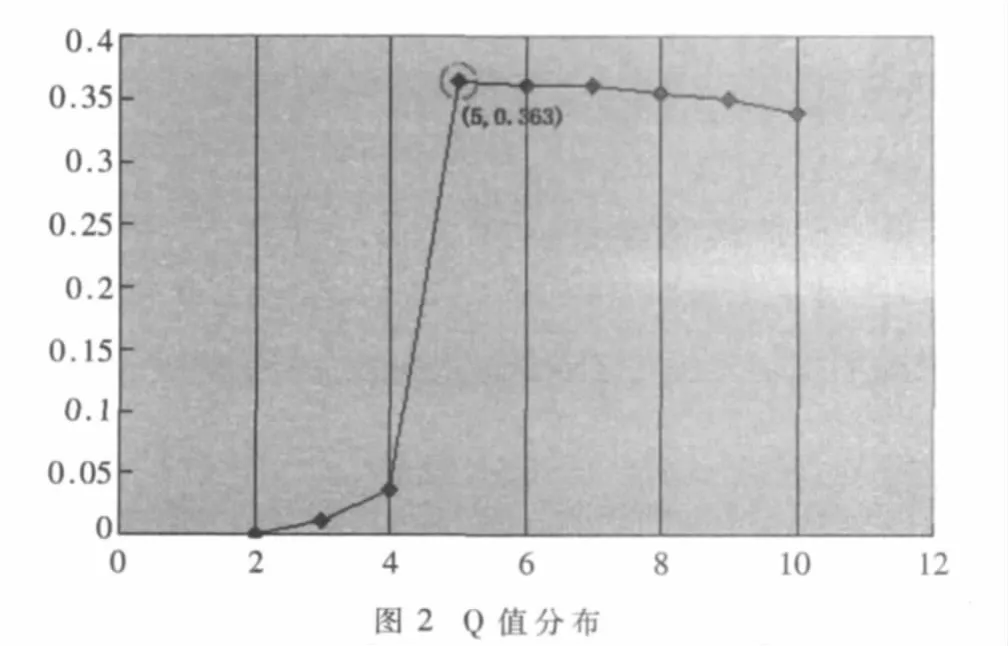
由图2可见,当Q值取最大0.363时,对应的社区个数为5,此时划分质量最高,网络中社区结构图如图3所示。
3.2 “Zachary空手道俱乐部网络”中的算法应用
Zachary空手道俱乐部网络[8]是测试社区挖掘算法的经典网络,该网络描述了美国一所大学空手道俱乐部的34名成员之间的关系,其中包含了两个已知的社区结构。图4的划分结果来自Girvan-Newman算法,不同社区用不同颜色顶点区分。

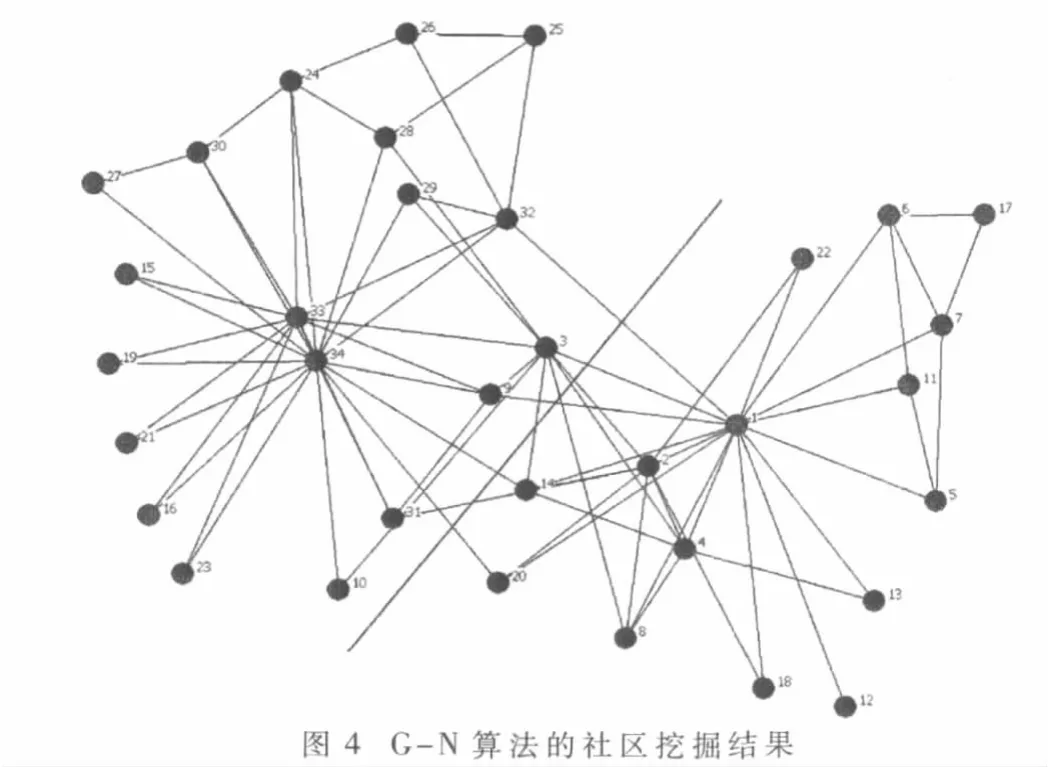
本文算法在选定Degree Centrality和海明距离分别作为ego角色探测和相似度计算策略后,划分结果如表1所示。
表1中,除了10,12,32,28四个顶点划分有误,其他都正确。在这种非EgoNetworks中,根据网络特征选取恰当的相似度计算和ego角色探测方法很重要,实验中选择了较简单的方法,虽然在准确性上有不足,但是时间复杂度只有 O(n),较传统方法的 O(n2),在大规模网络中,改进的层次聚类算法优势明显。

表1 改进的层次类聚算法的挖掘结果
社区挖掘是复杂网络分析的重要手段之一。本文总结了复杂网络中常用的顶点间相似度计算方法和顶点重要性度量方法,在此基础上,对传统的层次聚类算法进行改进,引入网络中“ego”角色的探测过程,并在现实的EgoNetworks以及经典实际网络中验证了算法的有效性。虽然改进的层次聚类算法能很好地提高社区挖掘效率,但是在准确性上仍有不足之处。如何提高算法准确度以及如何根据具体的网络特征,制定合适的相似度计算和“ego”角色探测方法是以后研究的主要工作。
[1]GIRVAN M,NEWMAN M E J.Community structure in social and biological networks[C].Proc.Natl.Acad.Sci.USA 99,2002:7821-7826.
[2]Yang Bo,Liu Dayou,Liu Jiming,et al.Complex network clustering algorithms[J].Journal of Software,2009,20(1):54-66.
[3]FORTUNATO S.Community detection in graphs[C].arXiv:0906.0612,2010.
[4]HANNEMAN R A,RIDDLE M.Introduction to social network methods[M/OL].Riverside,CA:Universityof California,Riverside,2005.http://faculty.ucr.edu/~hanneman/.
[5]ADAMIC L A,ADAR E.Friends and neighbors on the web[J].Social Networks,2007,25(2):211-230.
[6]NEWMAN M E J.Mathematics of networks[M].In The New Palgrave Encyclopedia of Economics,2nd edition.Palgrave Macmillan,Basingstoke,2007.
[7]NEWMAN M E J,GIRVAN M.Finding and evaluating community structure in networks[J].Physical Review E,69,2004.
[8]ZACHARY W W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1977,33(2):452-473.
- 网络安全与数据管理的其它文章
- 以太网供电技术在门禁系统中的应用

