基于贝叶斯网络的连锁故障概率模型

王 多，王维洲，靳 丹，于会泉，刘文颖

(1.甘肃省电力公司，甘肃 兰州 730050；2.华北电力大学，北京 102206)

基于贝叶斯网络的连锁故障概率模型

王 多1，王维洲1，靳 丹1，于会泉2，刘文颖2

(1.甘肃省电力公司，甘肃 兰州 730050；2.华北电力大学，北京 102206)

在分析连锁故障传播机理的基础上，按照连锁故障发生、发展的物理过程，分析系统潮流转移时线路的自临界特性，结合连锁故障发展阶段的概率特点，基于贝叶斯网络方法的连锁故障概率分析，建立了一种电网连锁故障的概率分析模型。通过对连锁故障过程的模拟，用系统负荷损失指标对连锁故障进行风险评估，分析系统的薄弱环节，研究降低连锁故障风险的预防策略。通过对我国某区域电网算例演示，验证了所构建的连锁故障概率模型的可行性、有效性。

连锁故障；电力系统；负荷损失；贝叶斯网络；概率分析

近年来，国内外发生的很多大停电事故都表现为连锁故障[1-2]，这类停电事故的共同特点是：开始往往是某一元件受到干扰，引起该元件正常工作的破坏，如果不能及时处理，随着时间的推移，造成事故的连锁性扩大，波及其他元件甚至整个系统，依次引起其他元件相继断开，最后造成大面积停电事故。这类事故发生的概率虽然不大，但危害极大，随着国内外对连锁故障问题认识的不断深化，如何构建合理的电网连锁故障模型已成为这一领域的众多专家学者所关注的焦点。

迄今为止，国内外学者在连锁故障研究领域做了大量的工作[2-4]。美国的Carreras、Dobson等学者开始采用自组织临界理论来解释电网的连锁故障问题，提出的OPA模型、CASCADE模型、HOT(Highly Optimized Tolerance)理论以及分支过程模型等是以复杂系统理论为基础并结合电力系统的实际而构造的[5-7]。文献[8]考虑了对包含传输线和发电机连锁故障的大规模停电事故进行定性模拟和分析的CASCADE模型。文献[9]描述了幂率关系的HOT理论，能够较合理地说明故障统计数据的初始分布规律。但这些模型也存在明显不足：这些模型实际上并不注重连锁故障发展过程的物理细节，而是强调电网发生连锁故障的初始条件以及电网发生连锁故障的长期宏观总体特性，是一种定性的连锁故障机理分析方法。

电力系统是一个复杂的非线性动态系统，系统中任一地点发生故障，都将在不同程度上涉及整个系统，正确的分析模型是对连锁故障进行定量分析并进而提出预防策略的基础。本文按照电网连锁故障的物理过程并结合各阶段事件的概率特点，充分考虑到网络结构的拓扑关系，以及系统潮流转移对线路元件间的不同影响，基于贝叶斯网络方法，结合电力系统中线路元件集群故障后的概率特性，建立了一种电网连锁故障的概率模型分析方法，并通过对连锁故障过程的模拟，用系统负荷损失等指标对连锁故障进行风险评估，找到系统的薄弱环节。文中通过我国某区域电网算例对所提概率分析模型和风险评估方法的合理性及其在电力系统中的应用进行了验证说明。

1 连锁故障传播机理

1.1 连锁故障发展过程

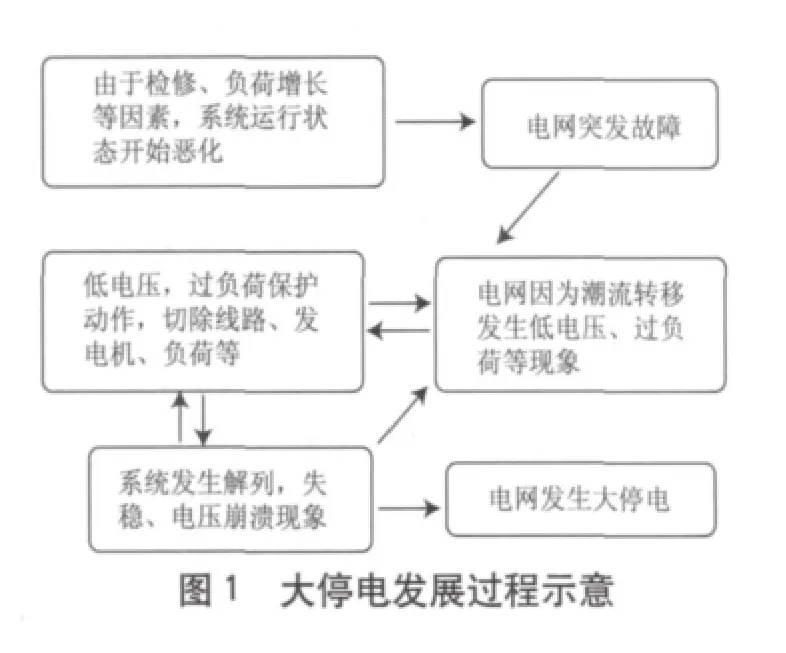
简单来说，连锁故障是由于系统中某一个元件故障，导致一系列其他元件停运的连锁反应，是一种发生概率较低但危害严重的事故。在很多大停电事故的初始阶段，潮流转移是使电网运行状态进一步恶化的主要原因，图1显示了大停电的发展过程。从图中可以看出，连锁故障的发展阶段是一个复杂的过程，其间伴随着低电压、过负荷、保护动作、解列和失稳，因此建立同实际电网相近的连锁故障模型是分析连锁故障的前提条件。

当电网发生元件故障时，由于线路故障后负荷的转移，使其他线路元件故障的概率上升，而自临界线路集群[10]的存在以及故障后对系统负荷转移的严重影响，使其余元件发生故障的概率更大。这样，当发生N-K故障时，由于网络存在自临界线路的情况，故障后使其余元件故障概率以幂指数上升，且自临界线路集群故障概率具有指数分布的特点，如果再考虑保护动作等隐藏故障，就有可能发展为连锁故障。

1.2 连锁故障的贝叶斯网络模型

从国内外电网大停电事故来看，连锁故障表现为保护动作导致的电力系统元件相继停运，连锁故障本质上是条件概率事件。贝叶斯网络[11]是基于概率分析、图论的一种不确定性知识的表达和推理模型，能够很好地表示变量的随机性、不确定性和相关性，非常适合条件概率事件的分析。

基于上述连锁故障机理的分析，连锁故障的发展过程主要为：系统初始故障后，电网发生潮流转移和元件过载，从而导致第一层激发事件，即线路过载跳闸或者保护误动；此后电网加速恶化，依次激发各层事件，线路集群分布故障扩大，出现线路集群自临界状态，最终导致大停电事故。以负荷被切除、发电机脱离系统以及电网解列作为连锁反应的终止条件，由此，可建立的贝叶斯网络模型连锁故障树如图2所示。

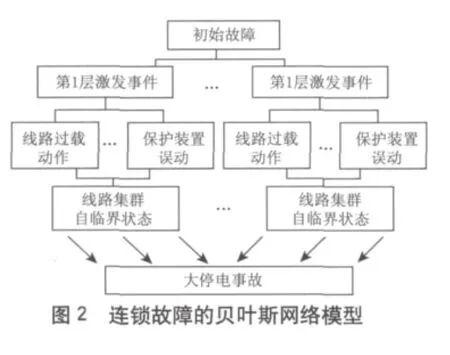
应用该故障树方法能够较清晰地表示连锁故障的发展过程。当一个线路元件被切除后，与该线路紧密相关的线路过载以及保护装置误动的概率[12]就大大提高，导致线路集群出现自临界状态是连锁故障发展过程的最主要形式。

2 基于贝叶斯网络的连锁故障概率分析

2.1 线路薄弱负荷的自临界特性

2.1.1 基于薄弱负荷指标的自临界线路集群

由网络结构拓扑分析，系统负荷薄弱性[13]严重导致了线路元件分布的不均匀性，线路薄弱连接加大了两节点之间元件的故障风险，使电力系统网络同时具备薄弱的聚集负荷和线路结构自临界特性，相关线路称为自临界线路。

由于自临界线路所带负荷的薄弱性，使得自临界线路故障，引起相关区域内其他自临界线路元件的故障概率大大提高，且随着故障后网络拓扑的变化，负荷的再分配可能会产生新的自临界线路，这些紧密相关的自临界线路集合统称为自临界线路集群。

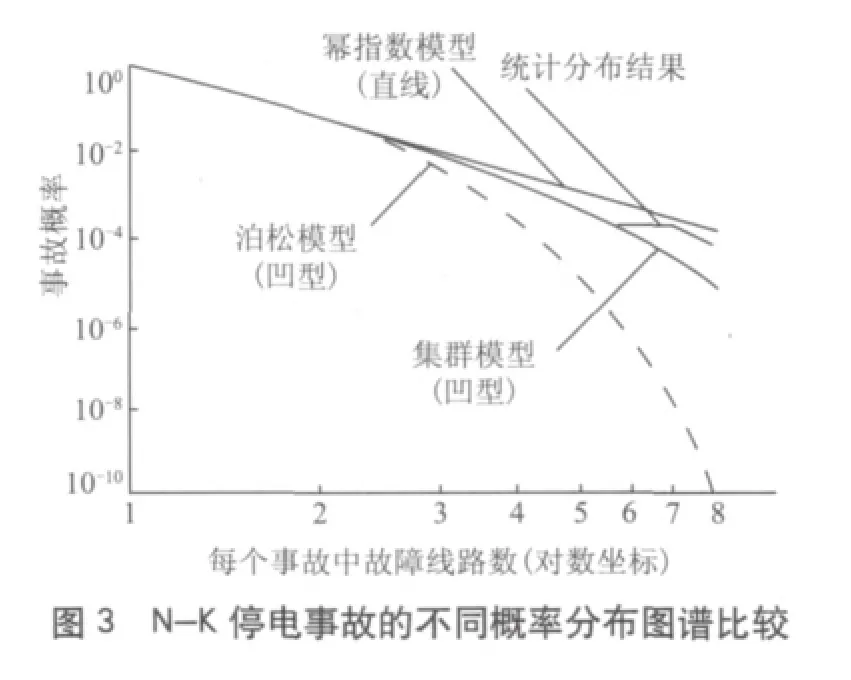
统计资料也表明，系统多条线路的集群分布故障是造成连锁故障的主要因素[10]，这正好能够更合理地从相关性上解释统计数据的分布规律，更符合电力系统实际的运行情况。为了对比，本文采用实际统计数据和泊松分布、集群分布和幂指数分布3种模型图谱，如图3所示。

2.1.2 自临界线路故障概率分布

由于自临界线路的故障后果很严重，所以考虑多重故障的情况，即线路断开后，至少会造成共同区域相连的所有线路中的某一条断开。由于同一区域内自临界线路之间存在必然的影响，且对连锁故障的发展最为严重，这里采用指数模型来表示自临界线路过载的动作概率，如图4所示。

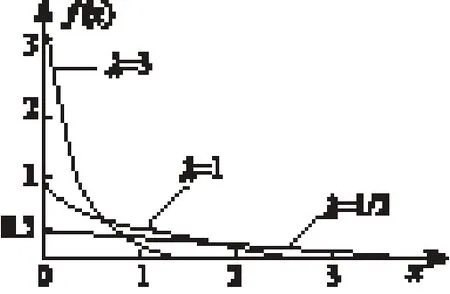
图4 指数模型的概率密度分布

对于指数分布E(λ)，连续型随机变量x的概率密度为：

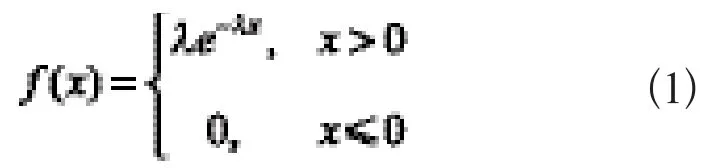
式中：λ>0为常数，则称x服从参数为λ的指数分布。

利用这一概率分布特性，充分考虑到网络结构的不足，把传输线路之间故障互相作用的概率进行定量化分析，提出了一种计及网络自临界线路集群的连锁故障概率分析模型。这个模型同实际电网运行状况相一致，更具有普遍意义，并验证了电网故障发展中薄弱负荷的存在。

自临界线路集群整合概率模型实际上是一种更为实用化的模型。其基本前提是，当系统受初始扰动时，考虑了不同元件上叠加相同的初始扰动量D，其中以集群形式分布的自临界线路的后果尤为显著；当某一元件停运并发生潮流转移时，自临界集群元件上叠加相同的转移量p等，这也极大地推动了连锁故障的演化发展。由于条件有限，只针对传输线路的自临界线路集群进行整合概率计算，分析电网的计及自临界线路故障的风险度。

2.2 基于贝叶斯网络的连锁故障概率模型

采用整合概率模型[14]来描述电力系统基于线路集群的连锁故障。设系统初始状态下第i条线路故障的概率为PLi，引起的故障使第k条线路上发生功率过载的条件概率为Pk(i)，线路集群中自临界线路为X条，线路i故障后自临界线路为Xi条，可以用离散概率分布[14]来表示故障发生在自临界线路集群的条件概率为PXi，同时定义引起的故障使第k条线路上发生功率过载的条件概率为Pk(Xi)，可以得到连锁故障概率Pevent为：

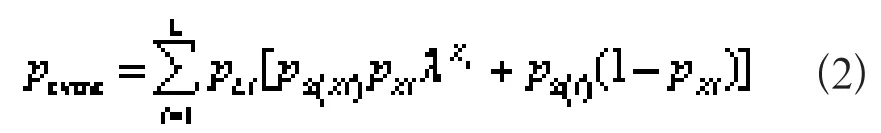
式中：λ为线路集群分布参数，取经验值1.5。

3 连锁故障的风险指标的确定

3.1 连锁故障终止条件

连锁故障终止条件是指在分析过程中需要确定结束连锁故障计算的条件，参照以下连锁故障结束条件。

(1) 某次计算后，潮流计算不收敛，加入控制措施也不能够收敛，则认为电网崩溃。

(2) 某次计算后，没有出现元件过载和电压越限的现象，也没有新的隐藏故障发生。

(3) 电网解列为2个孤岛，不包括单个负荷或者发电机的失去。

电网出现以上任何一种情况，则认为该次连锁故障搜索结束。

3.2 连锁故障失负荷的计算方法

线路上发生功率过载的严重程度是电网发生连锁故障的主要因素。用连锁故障发展过程中负荷损失总量指标的大小来度量连锁故障的严重程度，以系统损失负荷最少为目标函数：

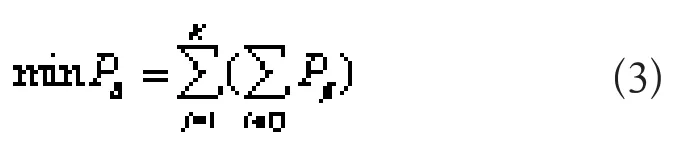
式中：K为控制措施的阶段数；Q为可切负荷节点的集合；Pji表示第j阶段负荷节点i上的切负荷量。

3.3 风险评估法

系统的风险指标定义为事故发生概率与事故严重度的乘积[20]，表达式如下：

式中：R为风险概率指标；Pe为事故概率；Ie为事故严重度。

连锁故障对整个系统造成的风险可通过负荷损失反映。对负荷的功率损失进行标幺化处理后，连锁故障负荷损失严重度指标为：

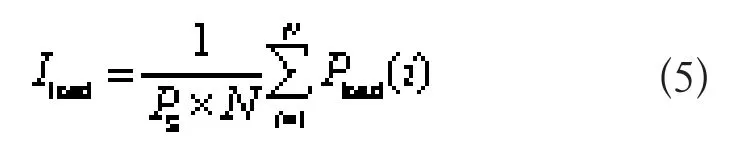
式中：N为故障数；Pload(i)为第i次连锁故障造成的负荷容量损失；Ps为系统容量。

根据公式(4)对风险指标的定义，连锁故障风险指标为：

由连锁故障的概率计算公式(2)，即可计算出系统连锁故障的风险指标。

3.4 连锁故障风险预防分析

应用上述连锁故障概率模型的相关理论分析和风险指标计算，将连锁故障分支的各个阶段用广义指数分布来模拟，并模拟自临界线路集群的故障概率。应用自组织线路概率模型的相关理论，结合CASCADE模型，可以用系统负荷的形式描述系统在设计和运行时，为避免连锁故障风险所必须遵循的基本原则，即合理发展电网结构，有效优化系统负荷分配，使线路集群处于工质参数在临界点以下的次临界状态，减少集群线路元件的数量，有利于减少电网连锁故障发生的概率，可限制故障传播从而降低连锁故障风险。

4 连锁故障概率模型算例分析

4.1 概述

以我国某区域电网2010年冬大负荷运行方式为例，该区域电网省际间联络线断面潮流如表1所示，电网采用西电东送极限方式。

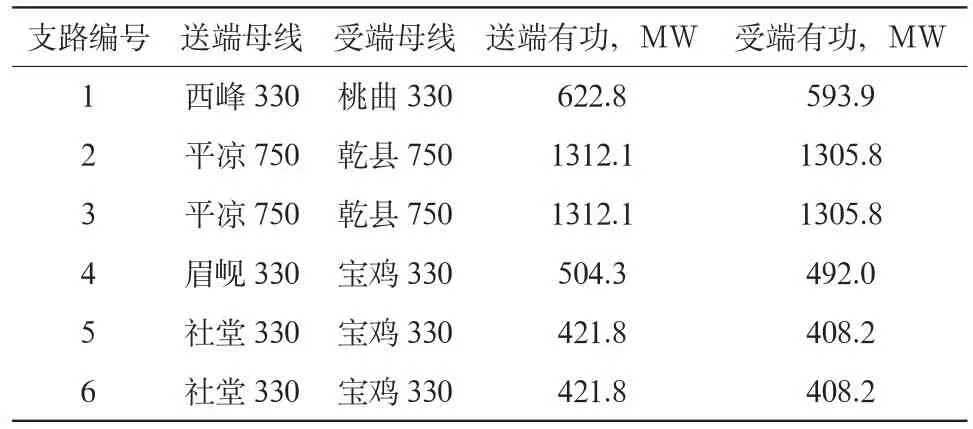
表1 区域电网省际断面潮流计算结果

4.2 电网算例分析

首先，利用综合程序PSASP对该区域电网进行故障扫描，确定平凉—乾县等线路故障为最危险，将他们设定为一级故障，用于后续故障的分析。

设定系统的初始潮流不变，计算线路故障引起的潮流转移。根据贝叶斯网络的连锁故障概率模型分析，得出可能的二级故障和相应的指标计算结果；经快速暂态扫描，再根据一、二级故障的信息，利用所给指标对剩余线路进行扫描，可确定三级故障风险指标高的线路；依据连锁故障终止条件，得到引发逐级连锁故障的概率Pevent和连锁故障路径上的总负荷损失Iload；按照连锁故障风险指标的计算公式，得到经归一化处理后逐级变化的连锁故障风险指标，结果示于表2。

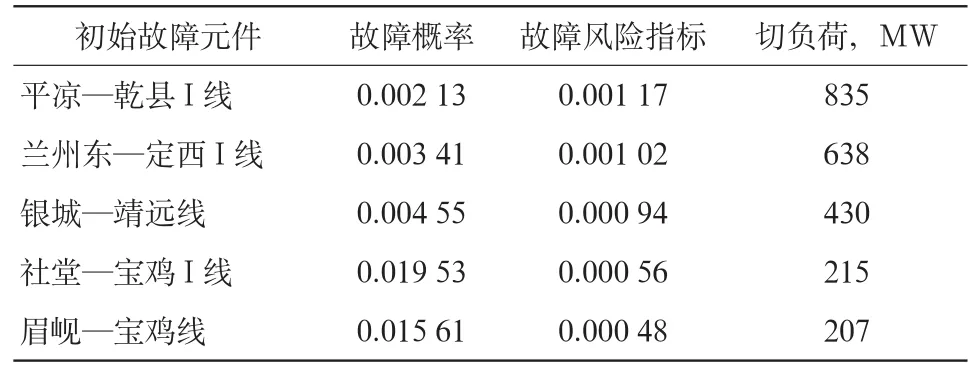
表2 连锁故障风险指标最大的5条线路

重复上述过程，可进一步确定系统更高级别的后续故障。通过这样的风险分析，可以直观地反映各级故障的发展过程中系统风险值的逐级变化及其对系统安全的影响。由表2可以看出，平凉—乾县线路发生同杆并架2级故障时，断面联络线过载运行，线路集群分布故障扩大，其切负荷数最大且故障威胁最为严重，显示了系统的脆弱环节。因此，如果此线路出现问题，运行人员应给予足够的重视并采取相应的措施。

5 结论

以故障概率分析为基础，引入自临界线路故障概率分析，提出了基于电网的贝叶斯网络方法的连锁故障概率模型。该过程模型是CASCADE模型的一种近似，结合了自组织临界模型和集群模型的实用优点，有效削弱了模型前提和现实条件之间具有差异的缺陷，因而是一种有效的连锁故障机理分析方法。它能更有效地控制电网故障的发展，便于及时发现系统的薄弱环节，为电力系统的控制和设计提供更加准确的理论依据。仿真算例进一步说明了文中所提模型及方法在电力系统中应用的合理性和有效性。

1 薛禹胜. 时空协调的大停电防御框架[J]. 电力系统自动化，2006，30(3)：1-10.

2 鲁宗相. 电网复杂性及大停电事故的可靠性研究[J].电力系统自动化，2005，29(12)：93-97.

3 Carreras B A，Newman D E，Dobson I，et al.Evidence for self-organized criticality in electric power system blackouts// Proceedings of th 34th Hawaii International Conference on System Sciences，January 3-6，2001，Maui，HI，USA，2001：705-709.

4 易 俊，周孝信. 考虑系统频率特性以及保护隐性故障的电网连锁故障[J]. 电力系统自动化，2006，30(14)：1-5.

5 Dobson I，Carreras B A，Newman D E. A probabilistic loading-dependent model of cascading failure and possible implications for blackouts//Proceedings of the 36th Hawaii International Conference on Systems Sciences，January 6-9，2003，Maui，HI，USA，2003 ：10-19.

6 邓慧琼，艾 欣，余洋洋，等. 电网连锁故障的概率分析模型及风险评估[J]. 电网技术，2008，32(15)：41-46.

7 孙 可，韩祯祥，曹一家. 复杂电网连锁故障模型[J].电网技术，2005，29(13)：1-9.

8 王明俊. 大电网继电自动装置的隐藏故障、脆弱性和适应性问题[J]. 电力自动化设备，2005，25(3):1-5.

9 Newman M E J，Strogatz S H，Watts D J.Random graphs with arbitrary degree distributions and their applications [J].Physical Review E，2001，64(2)：11-19.

10于会泉，刘文颖. 基于线路集群的连锁故障概率分析模型[J]. 电力系统自动化，2010，34(10)：29-33.

11 吴 欣，郭创新. 基于贝叶斯网络的电力系统故障诊断方法[J]. 电力系统及其自动化学报，2005，17(4)：11-15，40.

12 张国华，张建华，杨志栋，等. 电力系统N-K故障的风险评估方法[J]. 电网技术，2009，33(5)：17-21.

13 Fouad A. A，Qin Zhou，V. Vitttal. System vulnerability as a concept to assess power system dynamic security.IEEE Transactions on Power Systems，1994，9(2)：1009-1015.

14 胡泽春，王锡凡，张 显，等. 考虑线路故障的随机潮流[J]. 中国电机工程学报，2005，25(24)：26-33.

2011-04-13)