某地人工湖蓄水能力的论证研究

崔浩浩，田 禹，朱 喜，马杨敏，高宗军

(山东科技大学，山东省沉积成矿作用与沉积矿产重点实验室，山东 青岛266510)

为改善人们的生活环境、提高生活质量，某县政府研究决定在县北部建造人工湖，以保质保量、节约用水、生态环保、经济适用为目标，全力打造绿色环保生态花园。建设人工湖后，该人工湖的蓄水能力如何，渗漏多少，在现有的补给能力范围(5 000 m3/d)内能否保持人工湖的景观?针对这个问题，本文展开以下论证研究。

1 研究区概况

研究区的水文地质及地形条件简单。研究区为一个自北向南发育的小型沟谷，北东西为山丘，周围水位较高，对该区进行补给，形成了一个小型的聚水盆地。出露地层一般浅部为第四系残坡积土，厚度为1～2 m，下伏基岩为片麻状闪长岩，弱风化～全风化，裂隙基本不发育;在研究区区南部沟谷底部发育约150 m2的厚约1 m的砂层;部分区域有人工堆积土。区内构造简单，没有断裂发育，局部有挤压破碎现象。

结合实际地形地貌条件及水文地质条件，结合高程的差异等因素，拟在以下相应的位置建造四道堤坝，形成梯级式水面效果，依次呈阶梯状。这样既可以保证下级坝蓄水后，库水可抵达上级坝的坝脚，呈现最大水面效果，也可以产生若干个人工小型瀑布的景观效果。相应的具体建造水坝设计情况如图1所示。

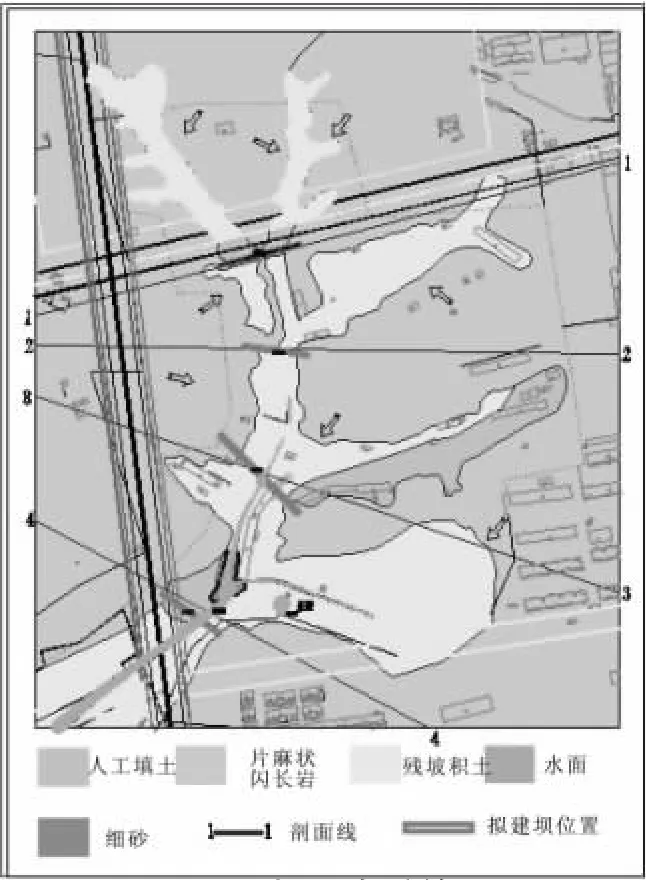
图1 水文地质简图

2 渗漏问题的分析

为论证该人工湖的蓄水能力，需要对渗漏问题进行分析。人工湖建坝蓄水后会通过坝、和湖区的透水层、透水带向下游及湖外渗漏，影响人工湖的景观效益。通过水文地质调查区内没有透水带，断裂等导水因素，且该区出露基岩为片麻状闪长岩，倾角较大，且走向与人工湖的流向基本垂直，加上水文地质调查周围的水位均比较高，有向该区汇聚的趋势，该故不考虑侧向渗漏的问题。因而渗漏的主要因素就是库底渗漏和绕坝渗漏。

图2 研究区的电子沙盘及拟建坝的位置

2.1 库底渗漏

2.1.1 渗透系数的确定

根据拟设的四道坝的位置，对每道拟设坝的库底区域选取适宜位置进行了渗透试验，来确定其渗透系数。渗水试验采取非稳定流渗水试验。

表1 人工湖四个不同区域的渗透系数

根据表中数据，取其平均值，得出:K=0.000 129 757 m/s=11.21 m/d

该渗透系数为库底基岩上覆松散沉积物的渗透系数，当人工湖蓄水时，先要饱和基岩上覆的松散沉积物，这部分损失的水不会漏失到人工湖以外，因为该覆盖层厚度不大，1～2 m，即使不挖掉对人工湖的蓄水能力也是没有多少影响的，只是在一定程度上延缓了人工湖蓄满水的时间，这样的渗漏叫暂时性渗漏，不能用来计算库底的渗漏。

在水文地质调查过程中，区内没有发现较大的、具有导水能力的断裂构造;该区强风化层厚度一般在1～2 m左右，考虑库区渗漏时，库底岩性应该被认为是弱风化或半风化、甚至新鲜基岩(变质岩)来看待，考虑库区基岩渗漏的时候，则参考了大量水文地质文献，并结合相邻地区基岩的渗透系数的经验值，确定K=0.025 m/d为库底或该区弱风化基岩的渗透系数，以此来计算库底渗漏。

2.1.2 库底渗漏的计算

为充分论证每一级坝的蓄水能力，要分别算出每一级库区的渗透量。

四道坝及所围人工湖的面积如表2所示。为了最大限度地利用好土地，发挥好城市土地的综合效果，建议将中间两个库区的面积缩小，增加休闲、娱乐、健身设施，以提高“湖区”公园的用途和价值。

图3 四道坝及所围人工湖的面积

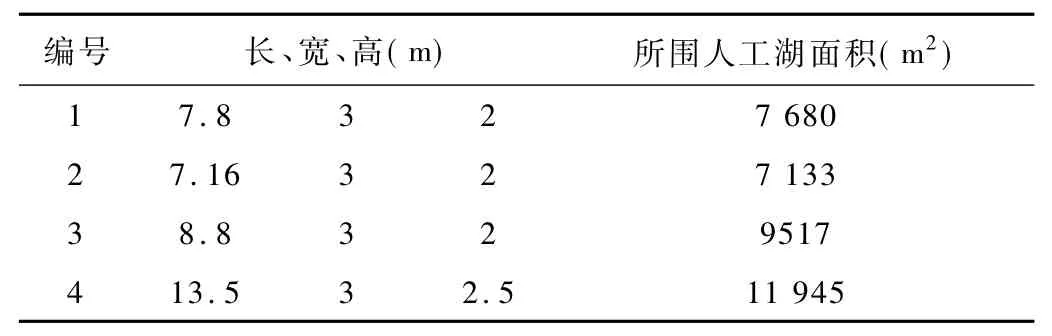
表2 回填处理之后四道坝及所围人工湖的面积

根据达西渗透定律:Q渗透=KAΔH/L

K为弱透水性基岩渗透系数;

A为过水断面面积，即人工湖面积;

ΔH为水头损失，(上下游过水断面的水头差)即两坝的高程差;

L为渗透途径，即上游到地下水位的距离;

库区一:根据达西渗透定律:Q渗透=KAΔH/L

K=0.025 m/d

A库一 =7 680 m2

ΔH=H+L1=3+9=12 m

L1=9 m

Q渗透=256 m3/d

库区二:根据达西渗透定律:Q渗透=KAΔH/L

K=0.025 m/d

A库二 =7 133 m2

ΔH=H+L2=3+6=9 m

L2=6 m

Q渗透=267.5 m3/d

库区三:根据达西渗透定律:Q渗透=KAΔH/L

K=0.025 m/d

A库三 =9 517 m2

ΔH=H+L3=3+3=6 m

L3=3 m

Q渗透=475.85 m3/d

库区四:由于库区四接近地下水位，向下渗漏量为0。

回填处理后的库区渗透量=256 m3/d+267.5 m3/d+475.85 m3/d+0=999.35 m3/d

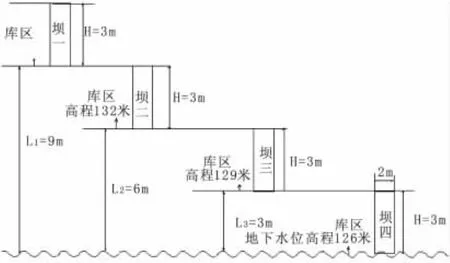
图4 库区渗漏计算示意图

2.2 绕坝渗漏量

绕坝渗漏又称坝肩渗漏，是指水库蓄水后，由于上下游水头差，使库水沿坝两岸岩石的孔隙、裂隙、溶洞、断层等向坝下游的渗漏。在实际情况中，由于基岩是弱透水性，一级坝除向下渗漏外还会绕坝渗漏，对下一级坝进行补给。在此约定，上一级库区水的绕坝渗透量，视为下一级库区的补给量。因此，我们计算的绕坝渗透量仅为第四道坝的渗透量(如图5)。

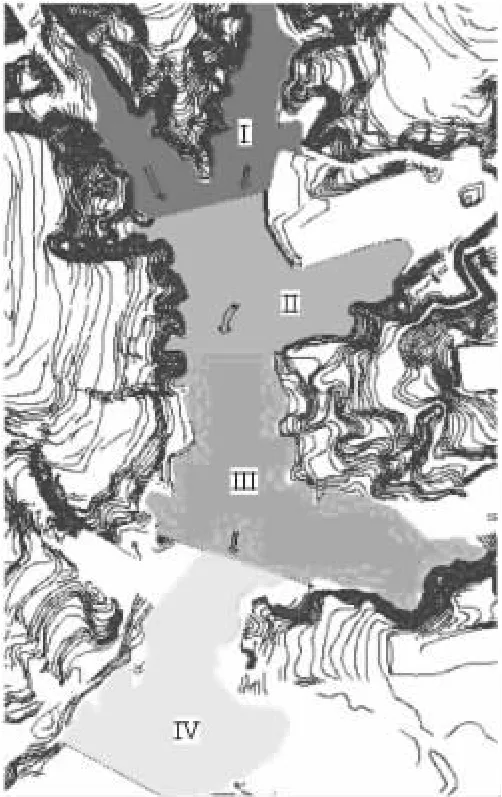
图5 库区相互补给示意图

在第四剖面上有泉眼露头，多年积水，高程为131.5 m，根据调查水位高程绘制出大体水位线如图6所示。

绕坝渗漏量:

Q=KΔb(H1+H2/2)H/L

式中:K为岩土的渗透系数;Δb为某一渗流带的长度;L为某一渗流带的宽度;H1为水库正常高水位至隔水层顶板的高差;H2为水库下游水位至隔水层顶板的高差;ΔH为水库上下游水位差;

公式中Δb(H1+H2/2)即为坝基两侧蓄水后透水断面的面积，在CAD中根据剖面四量出两侧透水断面的面积为14.2 m2+7.6 m2=21.8 m2

K为取绕坝试验中求得的四次渗透系数的平均值0.000 129 757 m/s=11.21 m/d;

ΔH为为水坝的高度3m;

L为为坝基的宽度2m;

Q=21.8 ×11.21 ×3 ÷2=122.189 m3/d

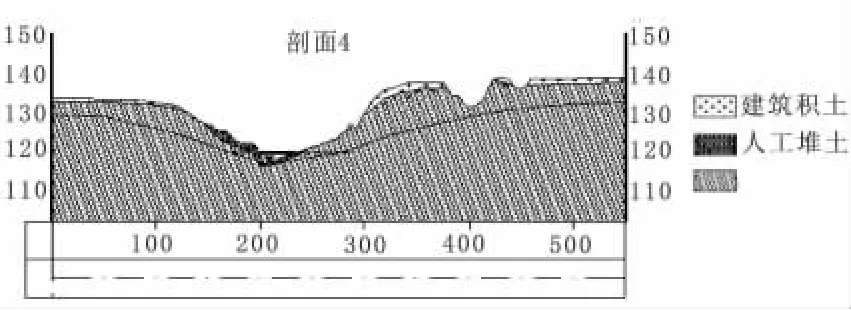
图6 第四道坝的剖面图

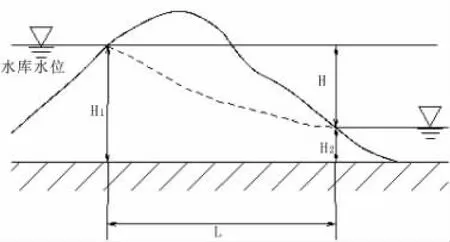
图7 绕坝渗漏计算示意图

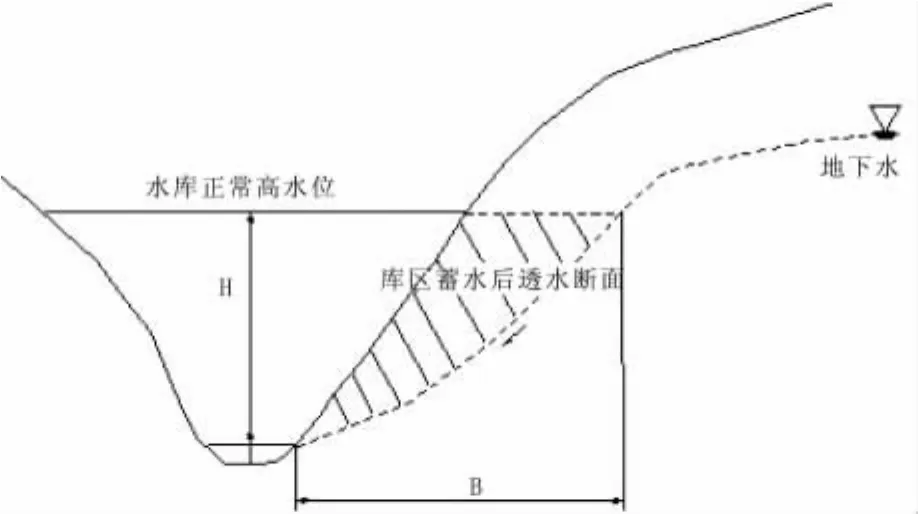
图8 绕坝渗漏带范围(蓄水后透水断面)

2.3 渗漏计算

整个人工湖的渗漏量计算公式如下:

Q补=Q库区渗漏+Q绕坝渗漏+Q降水－Q蒸发

其中 Q库区渗漏和 Q绕坝渗漏在上述计算中分别为999.35 m3/d和 122.189 m3/d

Q降水和Q蒸发通过收集当地资料分别为 Q湖降=134 m3/d和 Q湖蒸=213.7 m3/d

通过以上计算得出该人工湖每天需要的补给量是1201.239 m3/d。

3 结论

本文为验证人工湖的蓄水能力，对研究区的渗漏问题进行分析，确定了渗漏的主要因素为库底渗漏和绕坝渗漏，并分别计算出了相应的渗漏量，从而得出要维持该人工湖的景观效应需要的补给量是1201.239 m3/d，完全在其补给能力之内。