火工品发火可靠性小样本鉴定试验方法

田玉斌，王典鹏

(北京理工大学 理学院，北京100081)

火工品是武器装备的关键元件，其发火可靠性指标往往很高，如可靠度下限p =0.999，置信水平0.95.为了鉴定火工品的发火可靠性，目前使用的方法有计数法［1］、升降法［2］和计数--计量综合方法［3］。

计数法直接在工作水平处进行试验，基于二项分布模型给出发火可靠度的置信下限。计数法简单，所需样本量很大，如为了鉴定火工品的发火可靠度不低于0.999(置信水平0.95)，需试验2996 发火工品，且无一失效［1］。

升降法做如下假设: 1)每一产品存在一个固有的临界刺激量，当外界施加的刺激水平大于该临界刺激量时，产品发火; 否则不发火。2)产品临界刺激量X 的分布F(x)称为感度分布，常取

式中:G(·)为已知函数; μ 为位置参数;σ 为刻度参数。在升降法中，按照升降试验规则，获得发火或不发火数据;通过计算参数(μ，σ)的最大似然估计，求出火工品发火可靠度的点估计和近似置信下限。由于升降法使用了感度分布模型，样本量大大减小。但是，升降法的估计精度不高，往往高估火工品的发火可靠性。

在计数—计量综合方法中，首先利用升降法估计参数(μ，σ)，拟合感度分布。然后，基于该拟合分布，按照一定原理，寻找与工作水平等价的试验水平，该水平对应的发火率较低。最后，在该水平处进行试验，通过考察该水平处的发火率，等价地鉴定工作水平处的发火可靠性。为了鉴定火工品发火可靠度不低于0.999(置信水平0.95)［3］，计数-计量综合方法所需样本量在300 发左右。

遵循目前国际相关科学研究的前沿方向［4-5］，研究的热点不仅仅局限于鉴定火工品的发火可靠性，更多关注的是: 在中小样本情形，推断火工品以预定概率p 发火的刺激水平xp(也称为火工品100% p 发火点)，它满足

推断包括:给出xp的点估计和置信上限。这样的方法，不仅能够鉴定火工品的发火可靠性，而且能够定量给出火工品的作用裕度。

本文将基于估计xp的优化试验设计，给出xp的点估计和置信上限、作用裕度的区间估计、以及鉴定火工品发火可靠性的方法。最后，应用蒙特卡罗方法模拟研究上述方法的精确性。

1 鉴定火工品发火可靠性的优化试验设计

1.1 数学模型

假设火工品的感度分布如(1)式所示，对一产品施加刺激水平x，记试验结果:yx=1 为发火;yx=0 为不发火。在水平x 处进行试验，产品发火的概率

此时，xp=μ+σG-1(p).为了较精确地推断xp，应采用序贯试验设计［5］。假设(x1，y1)…(xn，yn)是对应的试验数据，其中xi为第i 次试验的水平，yi为试验结果，n 为样本容量。基于该观测数据，似然函数［6］为

式中:pi=G((xi-μ)/σ.对(4)式关于μ，σ 求导数，并求期望

构成Fisher 信息矩阵。该矩阵是试验数据包含(μ，σ)的信息的一种度量［7］。

1.2 推断xp的优化试验设计

根据文献［7］，在合理的试验水平范围内，优化分散试验水平，可以精确地估计参数(μ，σ).根据文献［4］，将试验水平逐步设置在xp附近，将提高xp估计的精度。文献［8］综合这2 种思想，给出3 段式优化试验设计。本文应用该优化试验设计，给出xp的点估计和置信上限、火工品作用裕度的区间估计、以及鉴定火工品发火可靠性的方法。

1.2.1 第1 段设计

第1 段设计的目的是: 合理确定试验水平的范围。首先，猜测μ 的取值范围(μmin，μmax)和σ 的值σg.以下将对(μmin，μmax)快速进行调整，使试验水平较对称地设置在μ 周围。

在x1=3/4μmin+ 1/4μmax和x2=1/4μmin+ 3/4μmax两水平进行试验，获得试验结果(y1，y2):

1)若(y1，y2)=(0，0)，在x3=μmax+1.5σg处进行试验，若y3=1，跳入第2 段设计; 若y3=0，在x4=μmax+3σg处进行试验。如此继续，直到某次试验结果为1 时，跳入第2 段设计;否则在上一次试验水平的基础上增加1.5 倍σg，继续试验，直到出现发火结果。

2)若(y1，y2)=(1，1)，在x3=μmin-1.5σg处进行试验，若y3=0，跳入第2 段设计;若y3=1，则在x4=μmin-3σg处进行试验。如此继续，直到某次试验结果为0 时，跳入第2 段设计;否则在上一次试验水平的基础上减少1.5 倍σg，继续试验，直到出现不发火结果。

3)若(y1，y2)=(0，1)，跳入第2 段设计。

4)若(y1，y2)=(1，0)，分别在x3=μmin-3σg和x4=μmax+3σg处各进行1 试验。然后，跳入第2段设计。

1.2.2 第2 段设计

第2 段设计的目的是:合理布置试验水平，优化模型信息。将该段设计分成3 部分，分别为寻找交错区间、加强交错区间和强化信息部分。

1)寻找交错区间。寻找交错区间分2 个步骤:

①计算出现发火结果的最小水平m1，以及出现不发火结果的最大水平M0.(a)若m1＜M0，停止试验，转至步骤2); (b)若m1＞M0，在σ =σg的条件下，求μ 的最大似然估计，并在该点进行试验，直至m1＜M0或m1-M0＜1.5σg.若m1＜M0，转至步骤2);(c)在m1-M0＜1.5σg，而且m1＞M0情形，分别在m1+0.3σg和M0-0.3σg处进行试验，如果出现不发火结果或发火结果，转至步骤2);否则，转至步骤②;

②令σg=2/3σg.更新①的m1和M0，并重复步骤①直至m1＜M0成立。

2)加强交错区间。如果M0- m1≥σg，则在(M0+m1)/2 处进行试验;如果0＜M0-m1＜σg，在(M0+m1)/2 +0.5σg和(M0+m1)/2 -0.5σg处各进行1 次试验。

3)优化模型信息。应用D 最优方法［7-9］分散试验水平，优化模型信息。①利用已观测到的试验数据(x1，y1)…(xk，yk)，计算(μ，σ)的最大似然估计(对该估计做如下限制性调整

式中: ak=min{ x1，…，xk}; bk=max{ x1，…，xk};②选择新的试验水平xk+1，使得Fisher 信息矩阵的行列式在(k，actual，k，actual)处达到最大; ③步骤重复①～②，直到完成预定样本量n1的试验。

1.2.3 第3 段设计

第3 段设计的目的是安排试验水平，使其更多、更快地聚集在xp附近。该段设计分为2 部分。

1)确定初始值。利用已观测到的数据(x1，y1)，…，(xn1，yn1)，计算最小试验水平xmin和最大试验水平xmax，求出μ 和σ 最大似然估计(，)，对其进行修正，即

2)优化逼近xp.在第3 段设计中，首先在xn1+1处进行试验。考虑如下形式的试验设计

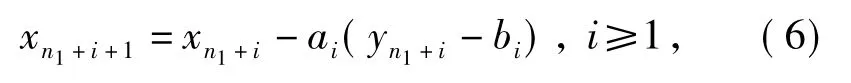
式中:xn1+i为第3 段设计的第i 次试验的水平; yn1+i为相应的试验结果; 且

式中:Φ(·)为标准正态分布函数; φ(·)为标准正态密度函数。

按(6)式和(7)式安排试验，直至完成容量为n2的试验。此时，xp的点估计为=xn+1，n=n1+n2.

1.3 火工品发火可靠性鉴定

假设火工品的工作水平为A，那么火工品的发火可靠度R 为该水平处的发火概率R=G((A-μ)/σ).按照文献［11 -12］，针对火工品的发火特性，作用裕度γ =(A -θ)/θ.定理1 在置信水平1 -α下，给出xp的置信上限AU，定理2 给出鉴定火工品的发火可靠度不低于p 的原理，定理3 给出γ 的区间估计。

定理1 利用(6)式和(7)式，获得试验数据(x1，y1)，…，(xn，yn).在置信水平1 -α 下，xp的置信上限为

式中:u1-α为标准正态分布的下侧1 -α 分位数。

证明1 令θ =xp.根据文献［4］，给定xn+1，θ的分布为由该分布，为了使

成立，AU需满足

定理2 利用(6)式和(7)式，获得试验数据(x1，y1)，…，(xn，yn).如果A≥AU，那么在置信水平1 -α 下，产品的可靠度R 不低于p.

证明2 根据定理1

1 -α=P(AU≥θ)，

于是，有

所以，

1 -α≤P(R≥p).

定理3 利用(6)式和(7)式，获得试验数据(x1，y1)，…，(xn，yn).则在置信水平1 -α 下，γ 的区间估计为

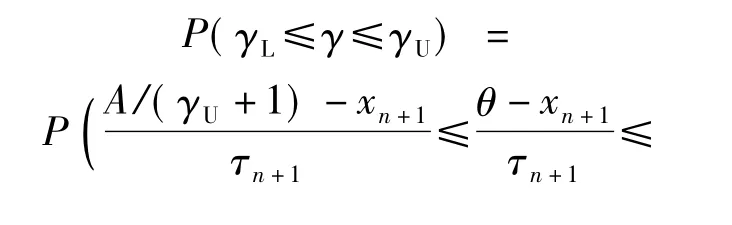
取

式中: uα/2为标准正态分布的下侧α/2 分位数;u1-α/2为标准正态分布的下侧1 -α/2 分位数。于是

2 模拟与应用研究

该节主要模拟第1 节提出的优化试验设计，给出火工品99.9%发火点x0.999的点估计、置信上限和该上限对x0.999真值的覆盖率。

2.1 模拟

在模拟研究中，假设感度分布为F(x)=Φ((x-μ)/σ)，μ =10，σ =1.此时，99.9%发火点的真值为x0.999=13.0905.按照优化试验设计规则，在试验前猜测μ 的取值范围(μmin，μmax)和σ 的值σg.在实际应用中，根据专家经验，对μ 的猜测一般较准确，对σ 的猜测波动较大。所以，在模拟中μg取9，10，11; σg取0.5，1，1.5，2 和3; (μmin，μmax)=(μg-3σg，μg+3σg);样本量n 取80 和100，其中第1 段和第2 段设计的总样本量n1=30，第3 段设计的样本量n2=50 或70.

在各种初始猜测下，模拟优化试验设计，获得容量为n 的数据: 计算x0.999的点估计xn+1; 在置信水平1 -α=0.95 下，计算xp的置信上限AU;将上述过程重复1 000 次，计算xp估计的均值，AU的均值，计算{θ＜AU}的频率，并与名义覆盖率1 -α =0.95 比较。模拟结果如表1～表3.

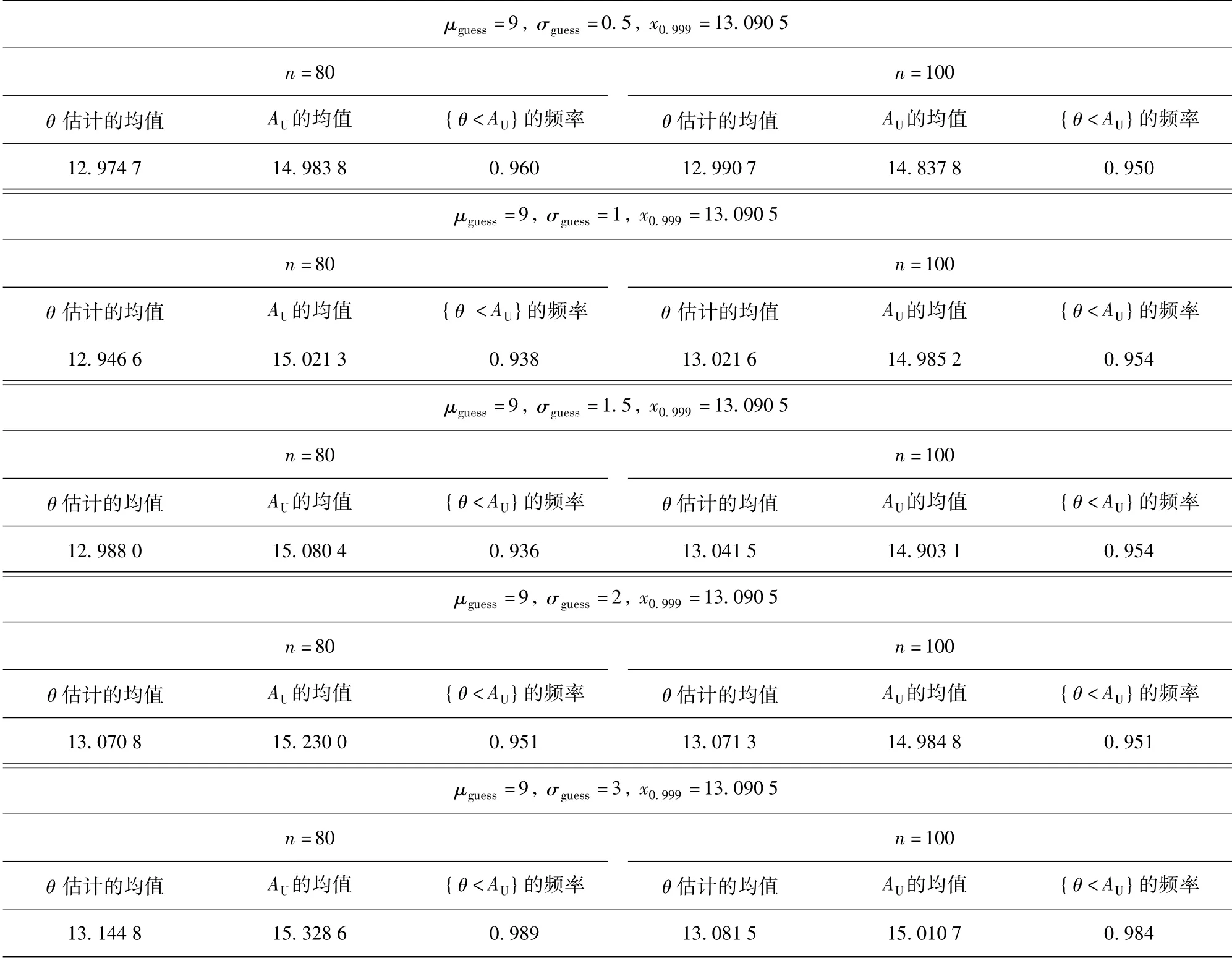
表1 μguess =9，σguess =0.5、1、1.5、2 和3 猜测下的估计结果Tab.1 Estimation results in μguess =9，σguess =0.5，1，1.5，2 and 3

表2 μguess =10，σguess =0.5、1、1.5、2 和3 猜测下的估计结果Tab.2 Estimation results in μguess =10，σguess =0.5，1，1.5，2 and 3

表3 μguess =11，σguess =0.5、1、1.5、2 和3 猜测下的估计结果Tab.3 Estimation results in μguess =11，σguess =0.5，1，1.5，2 and 3

2.2 模拟研究结论

从上述表格可知，针对火工品的高发火可靠性指标(置信水平0.95，可靠度下限0.999)，在样本容量n=100 时，在各种可能的初始猜测下，应用优化试验设计收集数据，给出0.999 发火点的点估计和置信上限，点估计与真值偏差很小，置信上限均高于真值且接近真值，覆盖率接近0.95 且高于0.95.这些都表明，应用本文提出的试验方法，在n=100 时，x0.999的点估计、置信上限、以及置信上限的覆盖率对初始猜测都是稳健的，点估计较精确，置信上限可信，其覆盖率大于0.95，表明置信上限略显保守。

综合而言，应用本文提出的试验方法鉴定火工品的发火可靠性，样本容量比现有方法大幅减小，结果可信且较精确。

References)

［1］GJB 376—87.火工品可靠性评估方法［S］.北京:国防科学技术工业委员会，1987.GJB376—87.Assessment method of reliability of initiating devices［S］.Beijing: National Standard Press，1987.(in Chinese)

［2］GJB/Z377A—94.感度试验用数据统计方法［S］.北京: 国防科学技术工业委员会，1995.GJB/Z377A—94.Statistical methods for sensitivity tests［S］.Beijing: National Standard Press，1995.(in Chinese)

［3］GJB6478—2008.火工品计数—计量可靠性评估方法［S］.北京:国防科学技术工业委员会，2008.GJB6478—2008.Variables-attributes synthetic assessment method of reliability of initiating devices［S］.Beijing: National Standard Press，2008.(in Chinese)

［4］Joseph V R.Efficient robbins-monro procedure for binary data［J］.Biometrika，2004，91: 461 -470.

［5］Joseph V R，Tian Yubin，Wu C F J.Adaptive design for stochastic rooting-finding［J］.Statistics Sinica，2007，17:1549 -1565.

［6］Silvapulle M J.On the existence of maximum likelihood estimators for the binomial response model［J］.Journal of the Royal Statistical Society，Ser B，1981，43: 310 -313.

［7］Neyer B T.A d-optimality-based sensitivity test［J］.Technometrics，1994，36: 61 -70.

［8］Jeff Wu，Tian Yubin.The optimal design for root finding with binary response data［C］.The First International Conference on the Interface between Statistics and Engineering，Beijing:Beijing University of Technology Press，2009: 9 -10.

［9］袁俊明，刘玉存.Neyer D-最优化的新感度试验方法研究［J］.火工品，2005，2: 24 -27.YUAN Jun-ming，LIU Yu-cun.Study on new neyer doptimal sensitivity test［J］.Initiators ＆ Pyrotechnics，2005，2:24 -27.(in Chinese)

［10］Tian Yubin，Li Guoying，Fang Yongfei.The synthetically analytical method for data sets on pyrotechnics reliability test［J］.J Sys Sci ＆ Math Scis，2006，26: 147 -158.

［11］Laurence J.Bement.Pyrotechnic system failure: cause and prevention［R］.NASA TM100633，Washington D C: 1988.

［12］王鹏，杜志明.火工烟火装置裕度研究与设计方法综述［J］.火工品，2005，2: 34 -38.WANG Peng，DU Zhi-ming.Summarize of margin research and design method of pyrotechnic devices［J］.Initiators ＆ Pyrotechnics，2005，2:34 -38.(in Chinese)