结合梯度信息的主动轮廓模型图像分割算法
张景辉,李 波,党长青
ZHANG Jing-hui,LI Bo,DANG Chang-qing
(唐山学院,唐山 063020)
0 引言
图像分割在计算机视觉和图像处理等应用中起着重要的作用。基于图像全局信息的主动轮廓模型Mumford-Shah模型[1]被提出以后日益成为图像分割领域中一种有效而强大的研究工具。Chan和Vese在Mumford-Shah模型和水平集方法[2]的基础上提出了一种图像分割模型—C-V模型[3]。该模型提出以后人们对其进行了深入的研究[4~6]。C-V模型具有很多优点,例如,可以得到全局最优解;能有效分割离散状的目标;分割结果对活动轮廓曲线的初始位置不敏感,等等。虽然C-V模型具有很多优点,但也有如下的缺点:1)由于δε(x)函数对远离活动轮廓曲线的目标边缘的抑制,使得C-V模型的分割速度非常慢。2)由于C-V模型仅利用一条闭合活动轮廓曲线分割图像,因此该模型只适用于分割具有一个目标的图像或者具有多个相同灰度级目标的图像,对于含有多灰度级目标的图像只能有效分割出强目标而弱目标则不能被正确地分割。针对C-V模型的上述缺点很多学者提出了改进方法。例如,李俊等[7]提出了用常数1替换δε(x)的改进方法。该改进方法虽然加速了C-V模型的分割速度,但也同时加速了活动轮廓曲线滑过弱目标区域的速度,从而加剧了过迭代和漏分割现象的产生。Song Gao等[8]提出了采用多个活动轮廓曲线分割图像的方法,该方法虽然能实现多灰度级目标的分割,但交替的进化多个活动曲线的计算量非常大并且计算结果也不稳定。
基于以上原因本文提出了把梯度信息引入C-V模型偏微分方程的图像分割算法。根据C-V模型完成图像分割时,目标区域像素点与背景区域像素点的水平集函数值的特征提出了一个基于梯度信息的加速因子。该加速因子可以有效地加速目标边界处像素点水平集函数值的进化速度,从而加速C-V模型的分割速度。根据水平集方法的基本原理和弱目标的梯度特征提出了一个弱目标区域控制项,该控制项可以快速稳定地锁定弱目标边界像素点的水平集函数值,使弱目标可以被快 速地,正确地分割。由于弱目标区域控制项可以使弱目标被有效分割,因此结合梯度信息的C-V模型只使用一条活动轮廓曲线就可以正确分割含有多灰度级目标的图像。
1 C-V模型分析
1.1 C-V模型
假设图像中每个同质区域的灰度是常数,设定义域为Ω的图像u0(x,y)被闭合活动轮廓曲线C划分为目标ui(C的内部inside(C))和背景uo(C的外部outside(C))两个区域,闭合活动轮廓曲线C内外像素的平均灰度值分别为c1,c2。考虑如下拟合能量函数:
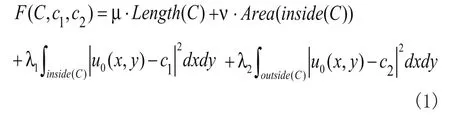
Length(C)是闭合活动轮廓曲线C的长度,Area(inside)(C)是闭合活动轮廓曲线C的内部区域面积,µ≥0,ν≥0,λ1>0,λ2>0是各个能量项的权重系数。只有 位于两个同质区域的边界时式(1)才能达到最小值。因此通过最小化式(1)就可以获得最终的图像分割结果。利用由初始闭合活动轮廓曲线得到的水平集函数φ(x,y),Chan和Vese把式(1)改写为:
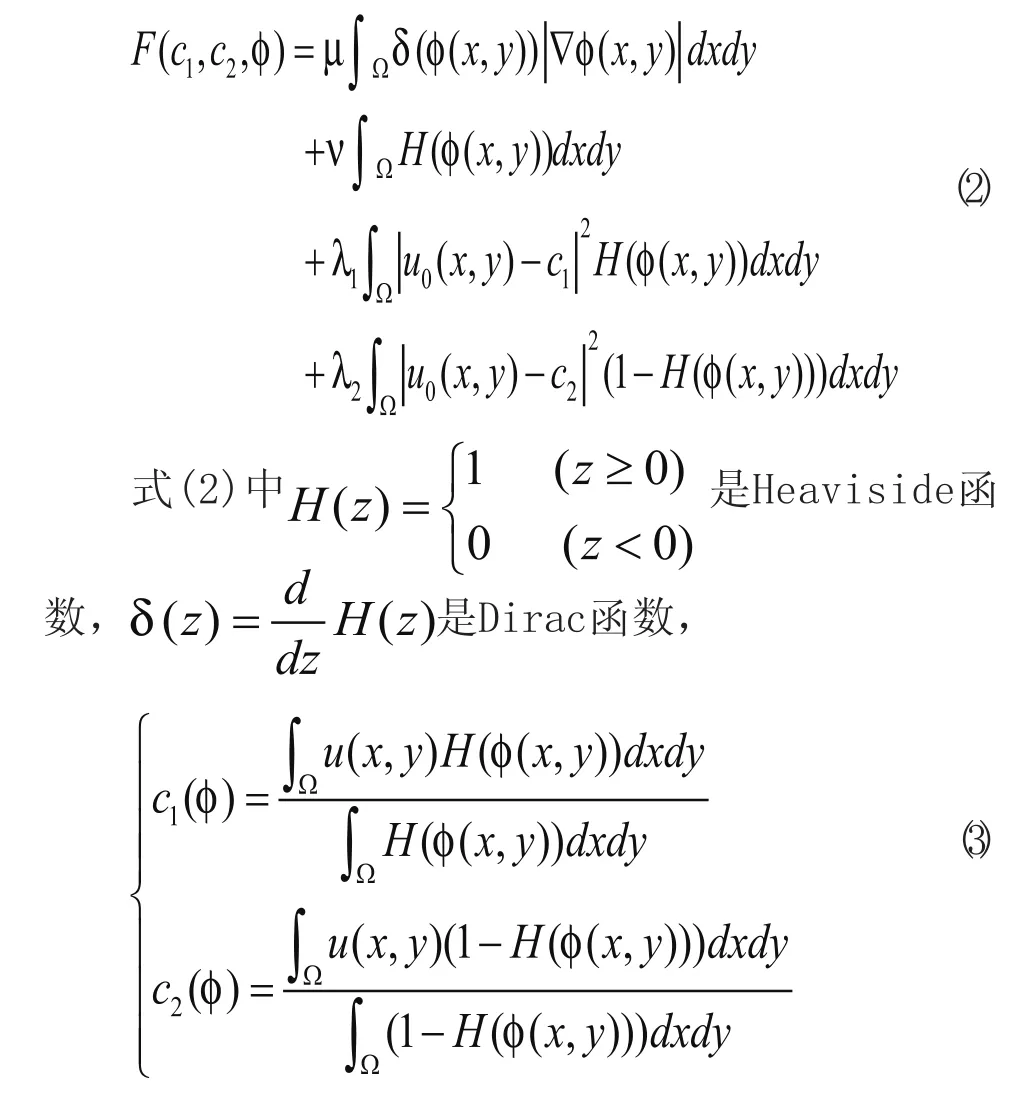
与式(1)相比,式(2)中的积分区间扩展到了图像的整个定义域。当式(2)表示的能量函数达到最小值时,就完成了图像的最终分割。
在最小化式(2)所示的能量函数时容易出现极小值的情况[9,10]。为了解决这个问题,Chan和Vese分别用规则化的Heaviside函数和规则化的Dirac函数代替Heaviside函数和Dirac函数。利用欧拉—拉格朗日法求解式(2)可得到以水平集函数 表示的如下偏微分方程:ε是大于零的参数,c1,c2由式(3)得到。通过迭代求解式(4)即可得到模型的解。
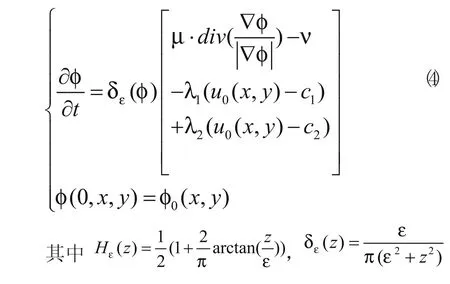
1.2 对C-V模型的分析
C-V模型之所以能有效地分割出带空洞的目标,是因为采用了规则化的Dirac函数:
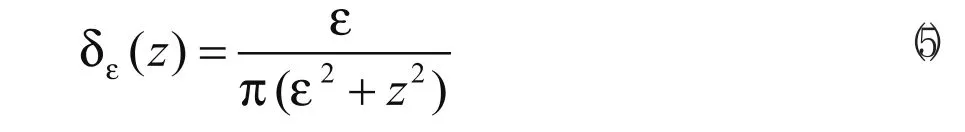
该函数保证在图像定义域范围内,所有点的函数值都是趋于零的正值,从而能检测出空洞区域中的异质区域边界。然而从式(5)可以看出当变量增加到某一数值时函数值δε(x)接近于零,并且不再有明显变化。因此该函数严重抑制了对远离闭合活动轮廓曲线的目标边缘的检测速度,致使C-V模型的分割速度非常缓慢。
由于C-V模型仅利用一条闭合活动轮廓曲线,因此该模型只适用于分割具有均质目标和背景的图像而对于分割含有多灰度级目标的图像则不能分割出与背景灰度级差别不大的弱目标。弱目标不能被分割可分为过迭代和漏分割两种情况。所谓过迭代就是在合适的迭代次数下可以把弱目标区域很好地分割出来,如果继续迭代的话,弱目标又被看作为背景。漏分割就是弱目标一直被看作背景无法被分割。
实验中发现在迭代求解方程(4)的过程中,水平集函数φ不收敛,使得很难设定一个迭代停止的标准(本文的仿真实验在生成符号距离函数时,在初始闭合活动轮廓曲线内部的像素点取正号,外部的取负号)。我们只能交互式的调整预先设定的迭代次数,当弱目标在初始活动轮廓曲线内部时容易产生过迭代,如图1所示。初始时弱目标在初始闭合活动轮廓曲线内部,则其 φ值为正数,图1(a)。在迭代的过程中可以检测到其区域的边缘,图1(b)。由于弱目标的灰度值与背景差别不大,c2的值接近弱目标区域像素点的灰度值,所以式(4)中的(u0(x,y)-c2)2要远小于(u0(x,y)-c1)2,因此式(4)中的右边会小于零,再经过几次迭代弱目标区域的 值就变成负值。初始闭合曲线就会滑过弱目标区域,从而该目标区域就被看成是背景区域了,图1(c)。弱目标在初始闭合活动轮廓曲线外部时则容易产生漏分割的现象,如图2所示。初始时弱目标的水平集函数值为负值,图2(a)。由于弱目标与背景的灰度值差别不大,在求解(4)的过程中其水平集函数值的符号没有发生改变,活动轮廓曲线不能演化到该区域的边界,如图2(b)所示。弱目标最终也不能被分割出来,如图2(c)所示。
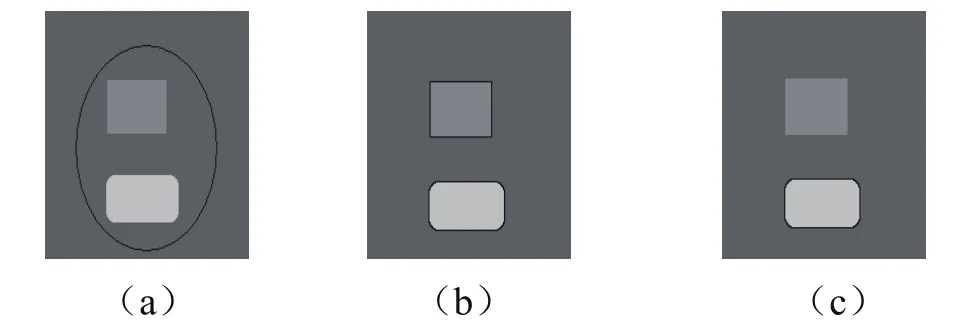
图1 过迭代现象
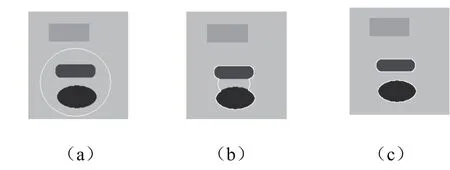
图2 漏分割现象
2 结合梯度信息的C-V模型及数值实现
2.1 结合梯度信息的C-V模型

图3 原图像和最终分割结果的水平集函数
根据C-V模型和水平集方法的基本原理可知,图像中的目标被正确分割时,目标区域像素点与背景区域像素点的水平集函数值的符号一定相反,如图3所示。(图3中第一行是初始活动轮廓曲线在不同位置的原图像;第二行是对应的最终分割结果的水平集函数。)另外,由于C-V模型所讨论的图像是近似分段常数函数,因此目标区域和背景区域的轮廓点与同质区域中其他像素点相比具有较大的梯度幅值。所以根据上述特征,我们引入梯度信息以加速目标和背景轮廓点水平集函数值的改变。当目标轮廓点与背景轮廓点的水平集函数值符号相反时也就可以完成对图像的分割。根据以上分析在方程(4)中加入基于梯度信息的加速因子:
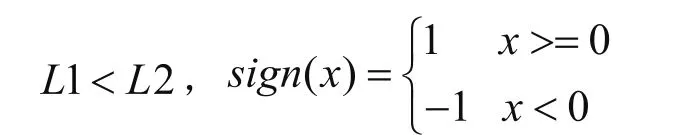
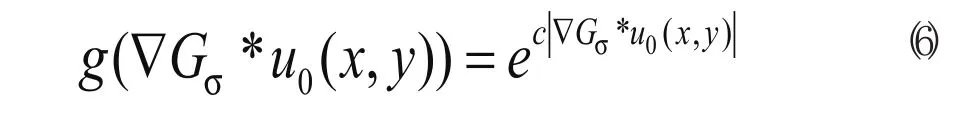
其中u0(x,y)为图像函数,Gσ是标准差为σ的高斯函数,‘*’表示卷积操作,是图像经过高斯函数卷积后的梯度,使用高斯函数卷积图像是为了平滑图像中的噪声,降低分割结果对噪声的敏感性,c是大于零的常数。
对加速因子做进一步分析:
由于图像中每个同质区域的灰度值是常数,在同质区域内部的像素点的梯度值为零,加速因子的值为1;目标和背景轮廓点的梯度幅值较大,这些像素点的加速因子可取得较大的值。由于同一幅图像在不同的环境下要求分割出的目标的细节不一样。c就是用来控制被分割的目标的细节程度。如果只分割主要目标,c的值可取的大一些(0.5-1)。如果要分割出细节目标,c应取比较小的值(0.1-0.5)。
为了解决C-V模型容易产生过迭代和漏分割的缺点本文考虑引入基于梯度信息的弱目标区域控制项。由水平集方法的基本原理可知,具有零水平集函数值的像素点两侧的像素点具有符号相异的水平集函数值。另外,弱目标轮廓点具有较小梯度幅值。根据水平集方法的基本原理和弱目标所具有的梯度特征,弱目标区域控制项应满足如下条件:
1)只对与背景灰度值差别不大的弱目标区域起作用。
2)能快速地使弱目标区域轮廓点两侧的像素点具有符号相异的水平集函数值并且水平集函数值不随着迭代的进行发生变化。这样活动轮廓曲线就可以快速地演化到弱目标区域轮廓点,并且随着迭代的进行活动轮廓曲线位置不会发生改变。
基于以上考虑,本文定义如下弱目标区域控制项:
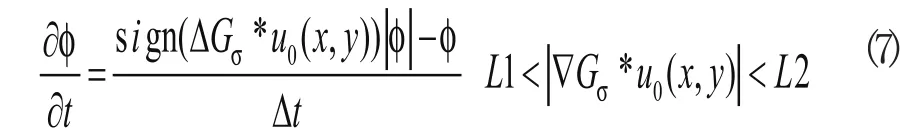
其中u0(x,y)为图像函数Gσ是标准差为σ的高斯函数,‘*’表示卷积操作,是图像经过高斯函数卷积后的梯度,是拉普拉斯算子作用于高斯函数卷积后的图像的结果,L1和 L2都是大于零的常数且
对弱目标区域控制项的进一步分析:
1)由于弱目标与背景的灰度值差别不大,弱目标区域轮廓点的梯度幅值就会很小,因此通过调整式(7)中L1和 L2的值就可以锁定弱目标区域的轮廓点。为了更精确的锁定这类轮廓点,可以根据梯度直方图来调整L1和 L2的值。
2)在图像的边界处,二阶导数有一个非常重要的性质,即目标边界两侧的二阶导数值符号相反。利用该性质和sign(x)函数就可以使弱目标轮廓点两侧的水平集函数值保持符号相异。
把式(7)和式(8)引入式(4)中就得到如下的结合梯度信息的C-V模型偏微分方程:
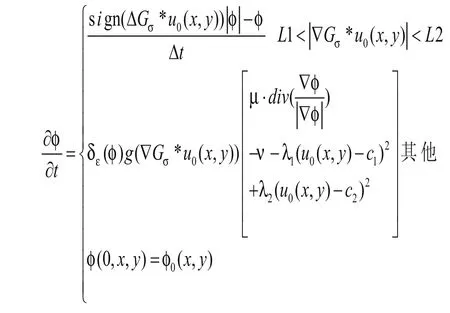
由上式可以看出加速因子有效加速图像中强目标的分割,弱目标区域控制项可以快速稳定的分割出弱目标。因此结合梯度信息的C-V模型,加速图像分割的同时也会提高C-V模型的分割精度。
2.2 结合梯度信息的C-V模型的数值解法
对图像u0(x,y)进行离散化,设h为离散网络的步长,(xi,yi)=(ih,jh),1≤i,j≥M为格点坐标,M为图像离散后最大坐标,∆t为时间步长,φni,j=φ(n∆t,xi,yi)是φ(t,x,y)的近似,这里有n≥0,
φ0=φ。0

根据边缘的特征可知边缘点亮的一侧拉普拉斯算子的值为正,暗的一侧为负。由式(9)可知无论弱目标在初始闭合曲线的外部还是内部,紧挨弱目标边缘点两侧的像素点的水平集函数值大小相等符号相反,并且随着迭代的进行水平集函数值不发生改变。虽然根据式(9)求得的水平集函数不再保持为符号距离函数了,但这并不会影响分割结果的稳定性。这是因为在C-V模型中水平集函数即使不是符号距离函数也可以得到满意的分割结果[3]。
对于其他像素点的偏微分方程采用有限差分法求解方程,
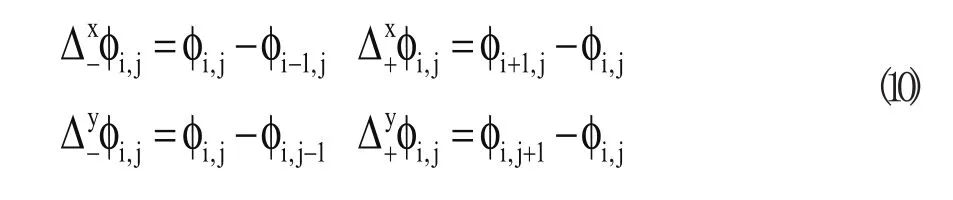
根据(10)将偏微分方程解的形式用离散化表示为:
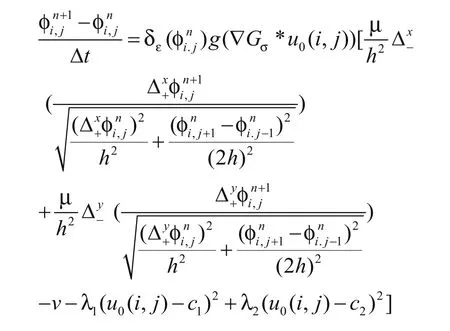
式中的c1,c2可由式(3)得到。
3 仿真结果
为了验证改进算法的有效性,我们对一幅合成图像和一幅自然图像进行了仿真实验,这两幅图像的尺寸都是 。图4所示为结合梯度信息的C-V模型和C-V模型对合成图像的分割结果。实验中参数:
图4(a)是原图像,弱目标在初始活动曲线的内部;图4(b)是C-V模型的迭代30次的分割结果,耗时0.6267s,已经发生了弱目标边界泄漏;图4(c)是改进的C-V模型迭代2次的分割结果,耗时0.0503s;图4(d)是结合梯度信息的C-V模型迭代100次的分割结果,没有发生弱目标边界泄漏;图4(e)是图4(d)对应的水平集函数,从图4(e)看出弱目标边界像素点的水平集函数值被稳定地锁定了。
图5所示为结合梯度信息的C-V模型和C-V模型对含有多灰度级目标的自然图像分割结果。实验中选择的参数为:
图5(a)是原图像,弱目标在初始活动曲线的外部(图像的底部所包含的目标为弱目标);图5(b)是结合梯度信息的C-V模型迭代18次的分割结果,耗时0.59s,弱目标已被有效地分割出来;图5(c)是C-V模型迭代500次的分割结果,耗时9.23,图像下半部分的弱目标没有被分割出来耗时9.23s;图5(d)是C-V模型迭代1000次的分割结果,耗时18.30s,弱目标仍然没有被分割出来。

图5 含有多个灰度级目标的自然图像分割结果
从图4和图5中的实验结果可以看出结合梯度信息的C-V模型不仅有效地解决了过迭代和漏分割问题,而且图像完成分割的迭代次数相对于C-V模型有很大的降低,图像的分割速度有显著的提高。
4 结论
梯度信息是图像所具有的基本特征之一,本文在对C-V模型容易产生过迭代,漏分割和分割速度慢的原因详细分析基础上,提出了把基于梯度信息的加速因子和弱目标区域控制项引入到C-V模型偏微分方程中的图像分割算法。弱目标区域控制项可以快速稳定的锁定弱目标边界,从而可以有效地解决过迭代和漏分割问题,也就是说仅利用一条活动轮廓曲线就可以有效地分割含有多灰度级目标的图像。基于梯度信息的加速因子可以著地提高图像的分割速度。实验结果表明了所给算法的有效性。
[1]Mumford D,Shah J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Communications onPure and Applied Mathematics,1989,42(5):577-685.
[2]Malladi R,Sethian J.A,Vemuri B C.Shape Modeling with Front Propagation :A Level Set Approach[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(2):158-175.
[3]Chan T,Vese L.Active contours without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.
[4]侯叶,郭宝龙.基于图切割与C-V模型的运动目标分割[J].光电子·激光 ,2008,19(12):1662-1665.
[5]王斌,高新波.基于水平集接力的图像自动分割方法[J].软件学报,2009,20(5):1185-1193
[6]尤建洁,王平安,夏德深.结合活动轮廓模型的无监督纹理图像分割[J].计算机辅助设计与图形学学报,2006,18(12):1897-1903.
[7]李俊,杨新,施鹏飞.基于Mumford-Shah模型的快速水平集图像分割算法[J].计算机学报,2002,25(11):1175-1183.
[8]Song Gao,Tied D.Bui Image Segmentation and Selective Smoothing by Using Mumford-Shah Model[J].IEEE Transactions on Image Processing,2005,14(10):1537-1549.
[9]Suk-Ho Lee,Jin Keun Seo.Level Set-Based Bimodal Segmentation With Stationary Global Minimum[J].IEEE Transactions on Image Processing,2006,15(9):2843-2852.
[10]陈波,赖剑煌.用于图像分割的活动轮廓模型综述[J].中国图象图形学报,2007,12(1):11-20.

