政府补贴对引资竞争的作用研究——基于技术外溢和跨国公司研发投资的模型分析

林 江，秦 军，黄亮雄，孙 辉＊

(1.中山大学 岭南学院，广东 广州 510275;

2.中国航空工业集团公司 第六三一研究所，陕西 西安 710068)

一、引 言

面对各地区的引资竞争，FDI如何选择落户地区，引起了学者的广泛研究。Tiebout提出的“以脚投票”［1］模型可谓是政府利用政策及公共物品吸引“外来人”的最早模型。Haufler和Wooton的研究认为，各国提出的吸引外资的优惠政策对跨国公司的投资区位选择没有任何正面影响，纯粹是资源浪费［2］。Barros和Cabral则通过建立一个两地区竞争一家跨国公司投资的动态博弈模型对此问题进行了研究。他们得出这样的结论:假定两个吸引跨国公司投资的国家即使不提供优惠政策，跨国公司也会在其中一个国家投资时，“囚徒困境”效应会使两个国家竞相提出各种吸引外资的优惠政策［3］。Fumagalli进一步研究了在技术外溢和两国技术差距对竞争FDI的影响。他同样假定跨国公司在没有任何补贴下也会选择在其中一国投资，他得到了与Barros和Cabral相类似的结论。他认为与未有政府补贴情况相比，两地竞争FDI是有可能提高两地的福利。而且，只有当两地区技术水平差距足够大时，两地间竞争FDI才能增加两地区的整体福利，并且技术差距越大，增加的整体福利就越多［4］。

岳中刚在Barros和Cabral(BC模型)的基础之上对此问题进行了更进一步研究［5］。他同样建立了一个两地区竞争一家跨国公司投资的三企业动态博弈模型，并且放松了BC模型的假定，即跨国公司不必然在两地区之一的地方投资，增加了跨国公司可以选择出口的情况。通过动态博弈及福利分析，他得出结论认为较落后地区必然要支付更多优惠来吸引跨国公司投资，而就一国 (两地区)的整体福利而言，两地区间吸引外商直接投资的竞争使引进外资的成本过大，将导致福利损失。取消较发达地区吸引外资的优惠政策，给予到欠发达地区投资的跨国公司将是一国整体福利改进的好措施。

Kuemmerle通过对跨国公司海外研发的类型进行区分，研究了不同类型海外研发的运作动机［6］。他指出技术增长型 (HBA)的研究机构为了获得新的知识资源，必须位于科技人才密集地区;而技术利用型 (HBE)的机构则是开发母国创造的技术优势，迅速将研究成果商品化，开拓国际市场，一般临近主要市场和生产性企业。Kumarz通过对美国和日本跨国公司海外研发活动的研究，得出结论认为研发区位选择的三个决定因素是巨大的国内市场规模、充足的低成本研发人员和国家技术能力的规模［7］。Fors和Zejan通过对瑞典跨国公司海外研发活动的研究，发现瑞典跨国公司倾向于将海外研发投资布局在行业内技术水平较高的地区［8］。

国内学者同样进行了不少针对跨国公司海外研发区位选择的研究。郑京淑的区位选择两阶段理论认为跨国公司R＆D区位决策分为两个阶段:第一阶段是目标国家选择，重点考虑R＆D资源丰富、研究运营效率较高的国家，研究成果可直接应用到设在东道国的生产性子公司从而直接实现市场效应的国家;第二阶段是目标国家内部区域选择，将重点评价人才环境，信息集聚环境，研究辅助环境，产品化环境等［9］。喻世友等专门对跨国公司研发投资的国别选择进行了研究，结果显示跨国公司海外研发投资高度依赖东道国提供必要的技术资源和当地技术资本的能力。跨国公司为保持发达国家和发展中国家之间的技术差距，大都把研发投资聚集在发达国家。市场规模同样也是决定投资区位的重要因素［10］。

上述对各地区之间引资竞争的研究都未考虑跨国公司进行研发活动的情况，而研究跨国公司海外研发的区位选择又未考虑到地区间引资竞争的影响。而事实上，跨国公司的研发活动不断影响到其自身的投资选择，而且也会影响到地区间的引资竞争。因为相比于普通的FDI，研发类的FDI更能产生技术外溢作用，这可能引起地区间更大的竞争。也就是说，针对该情况，R＆D、跨国公司与引资竞争三者是密不可分的，任意忽视其一，都有所欠缺。

二、基本模型

假定有A、B两个地区，且A为较发达地区，B为欠发达地区，跨国公司M选择在其中某一地区进行含有成本缩小型研发活动的投资。在两地区各有一家本地企业与跨国公司生产相同的产品。具体设定如下:

1.A、B两地市场规模相同，且地区之间不存在贸易成本和价格歧视，为一体化市场。因此，可以设定在这个一体化市场上该产品的需求函数为:

其中，P表示市场价格;Q表示一体化市场的产品总产量。

2.A、B两地区的本地公司及跨国公司M的可变生产成本分别为CA、CB、CM，且，CM≤CA≤C≤。成本小于1/3是保证在没有外商投

B资状态下，A、B两企业能长期正常运作即利润为正。

3.跨国公司M的决策集为 {投资A地区，投资B地区}，即跨国公司M只在且必在一个地区投资。对外直接投资的初始投资成本与产量规模无关，假定为0。跨国公司M与A、B两公司在A、B地区组成的一体化市场上进行策略为产量的古诺垄断竞争博弈，市场上的总产量为A、B、M三家公司产量之和:Q=qA+qB+qM。

4.跨国公司进行研发活动，且所进行的研发活动为成本缩小型，成本缩小额为X，从事此成本缩小型研发活动所付出的总投入可以表示为:

其中，r为研发活动的效率，r的值越大，表明为了减少一定单位的成本，需要付出更多的投入，反之亦然;X的平方形式表明随着成本缩小额的增多，所需投入要以几何倍的速度增加。在进行研发活动后，跨国公司M新的可变成本就变化为:NCM=CM－X。

5.存在技术外溢，并且跨国公司的技术外溢仅对其投资的地区有正的外部性。当地公司可以部分或者全部地获得跨国公司的技术，使其生产成本减少Φ (Ci－NCM)，由此，当地公司生产成本变为:

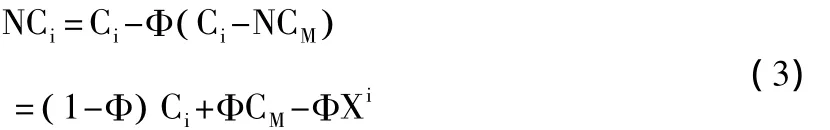
其中，Φ为技术溢出参数，0＜Φ≤1。当Φ=1时，技术溢出效应最强，当地公司将达到与跨国公司相同的成本水平。A、B地区都具备跨国公司先进技术的劳动技术和基础设施水平，并且与跨国公司技术水平差距越大，当地企业从技术溢出中获益越多。

6.将研发因素引入模型后，跨国公司和获得投资地区的当地公司利润函数表达式分别为:

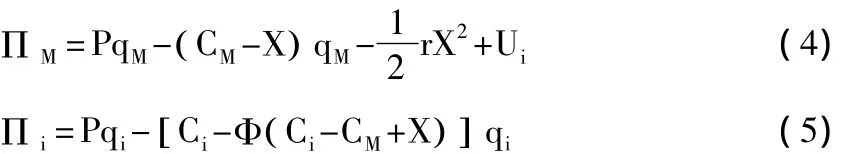
跨国公司能够进行研发活动使得成本缩小，为了吸引到此跨国公司直接投资，A、B两地区都提供可置信的补贴政策承诺，用Ui(i=A，B)表示。A、B两地区政府的目标函数为总福利水平，即消费者剩余与生产者剩余之和减去补贴成本。

动态博弈的过程如下:

第一阶段，A、B两地区政府同时承诺本地对跨国公司M的补贴额;

第二阶段，跨国公司M选择投资于A或B地区;

第三阶段，跨国公司M根据利润最大化原则确定研发投资所达到的最优成本缩小额;

第四阶段，A、B两企业与跨国公司M在A、B两地区组成的一体化市场上进行策略为产量的古诺垄断竞争博弈。

三、三企业产量、外商研发投资策略及政府政策的选择

针对此类完全信息动态博弈，采用逆向归纳法来分析，四个阶段的具体情况如下:

(一)第四阶段

跨国公司M已经既定在某一地区投资，并且研发活动的成本缩小额X也已经确定，在古诺竞争下，可以计算出A、B、M三企业的利润最大化下的各种变量。

若跨国公司M选择在A地区投资，三企业利润分别为:

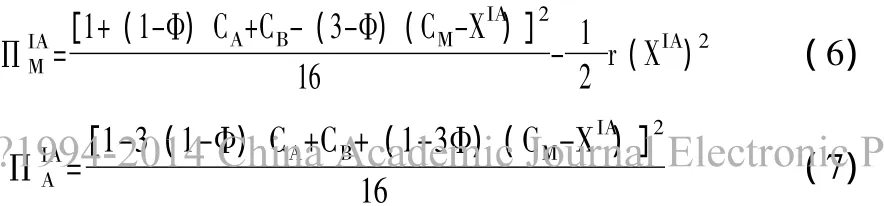
(三)第二阶段

根据A、B地区公布的吸引外资的补贴政策，跨国公司决定在A或B地区投资。由于跨国公司在两地区投资都没有初始投资成本，因此，在没有补贴或者两个地区补贴相同 (UA=UB)的情况下，跨国公司选择在A地区直接投资与在B地区直接投资的利润差额为:

从而得到命题一。

命题一:假设其它条件完全等同，并且没有补贴或者两个地区补贴相同，在存在技术外溢下，从事成本缩小型研发活动的跨国公司总会选择在生产技术较先进的地区进行投资。

这一点与跨国公司不进行研发活动的岳中刚的结论是一样的。

因此对于技术落后地区而言，如果想吸引此跨国公司的投资，就必须为跨国公司提供额外的补贴额，最小额为ΔΠM。而这个补贴额又随着落后地区相对于发达地区的技术差距的扩大而增大 (∂ΔΠM/∂(CB－CA)＞0)。

这是因为当两地间技术差距越大，跨国公司的技术在技术落后地区的外溢就越多，从而越能提高东道国企业在市场上的竞争力，使得跨国公司的利润相对受到压缩。但是在不存在技术外溢状况下，跨国公司在两地投资所获得的利润将是一样的。因此在技术外溢条件下，对于跨国公司的在A、B两地区之间的选择主要看A、B两地政府提供的补贴额的政策。如果UB＞UA+ΔΠM，跨国公司将选择在B地区投资;如果UB＜UA+ΔΠM，跨国公司将选择在A地区投资;如果UB=UA+ΔΠM，A、B两地区将各获得50%的投资机会。

(四)第一阶段

A、B两地区政府确定自己的补贴政策以竞争跨国公司的研发投资。

因为A、B两地区政府的目标函数为本地区的福利水平，因此两地区政府所能提供的补贴额并不是无限增大，而是要受到约束的。约束条件就是两地的福利水平变化情况。两地区政府所能提供的最大补贴额为跨国公司投资在本地区与投资在另一地区相比本地所获得的福利增加额，也就是:

在此情况下，当技术落后地区所愿支付的最大补贴额大于技术先进地区，并且足以弥补跨国公司在两地投资利润差额ΔΠM时，其才能争取到跨国公司投资;反之，技术先进地区将获得跨国公司投资。也就是:

其中，Ω为跨国公司的投资判断指标，它表示在两地政府在给予最大补贴额下，跨国公司投资B地区与投资A地区的利润差额，为正时，投资B地区利润大于投资A地区。①可以证明ΔCS=CSIBA－CSIAA=CSIAB－CSIBB＞0，且ΠIAA＞ΠIBA，ΠIBB＞ΠIAB。

命题二:若存在两地区的中央政府，且中央政府把两地整体福利最大化作为政策目标，那么由中央政府决策与两地自由竞争相比，跨国公司的投资地点选择不会改变。

证明:我们已知，当Ω＞0时，两地间自由竞争情况下，B地区将会获得跨国公司投资。Ω＞0，即 Ω=MAXUB－MAXUA－ΔΠM＞0，根据上面可知，(+)－+)－ΔΠM＞0，即在未给补贴情况下，投资在B地区的两地总福利与投资在A地区的两地总福利差额大于跨国公司投资两地的利润差额，此时，中央政府的决策将是给予投资B地区的跨国公司ΔΠM+ξ的补贴，并禁止A地区给予跨国公司补贴，此时，竞争结果将是跨国公司选择在B地区投资。反之，亦然。

这说明在两地竞争跨国公司投资的过程中，不论是地方政府自由竞争，还是中央政府决策，如果都是把本地或者整体福利最大化作为政策目标的话，最终的竞争结果将是一样的。不同之处在于中央政府决策过程可以减少由于竞争两地政府一味增加的补贴额，但不改变跨国公司对地区的选择。

命题三:不论是否竞争到跨国公司投资，对于技术落后地区，此竞争可以使本地福利水平保持不变或者改善;对于技术先进地区，存在竞争和禁止竞争时的福利水平差额则存在降低、持平和改善三种情况。①详细证明过程可向作者备索。

四、模型的模拟

(一)A、B两地区成本较近时的情况

A、B两地区的不同技术禀赋对两地竞争跨国公司研发投资会有不同的影响，我们首先考虑两地成本相近且较高 (即两地技术水平均处于较落后状况)时的情况。在此情况下，我们主要考察技术外溢率Φ与跨国公司的不同成本CM对跨国公司投资地选择以及社会福利的影响，因此可以假定两地企业初始成本和研发效率不变，我们可以得到图1。②关于参数的设定。CA=0.25，CB=0.30，r=10，Φ∈ (0，1)，CM∈ {0.05，0.1，0.15，0.2}。

图1 两地福利差额与跨国公司利润差额关系图

图1中虚线表示技术较落后B地区比技术较发达A地区愿意多支付的补贴额，即MAXUB－MAXUA;同时也表示在不考虑政府补贴时，跨国公司投资B地区与投资A地区两种不同情况下两地总社会福利的差额。MAXUB－MAXUA为正，表明与投资A地区相比，跨国公司投资B地区将使两地区总福利增加;MAXUB－MAXUA为负，表明跨国公司投资A地区使两地区总福利更大。图1中实线表示跨国公司投资A地区比B地区多获得的利润，即ΔΠM。在图1中，ΔΠM恒为正，表明在未有政府补贴时跨国公司在A地区投资获得的利润恒大于在B地区时的情况，这一点与上述命题一的结论是一致的。

我们可以看出，跨国公司的生产成本CM越大，虚线越高，说明B地区比A地区多愿意支付的补贴额在增加，这主要是由于在技术外溢率Φ一定的情况下，CM与CA越靠近，使得A企业利润减小幅度远大于B企业利润减小幅度，造成B地区从中获益;同时，跨国公司的生产成本CM越大，实线越低，说明跨国公司在A地区投资比在B地区可以多获得的利润随着其初始成本与当地企业越接近而变得越小。跨国公司在A地区可以多获得利润是由于与A地区相比，B地区初始成本较高，对于跨国公司来说，若投资B地区，B企业技术吸收较多造成本地企业竞争力增强幅度更大，相比之下，跨国公司利润变少;而跨国公司成本增加则可以减轻这种效果。

随着技术外溢率Φ的增大，ΔΠM也相应增大，说明在不考虑政府补贴的情况下，技术外溢率越大，跨国公司越倾向于投资技术较发达地区。这是由于与投资A地区相比，跨国公司投资B地区将使得当地企业获得成本缩小额相对较大，当地企业竞争力增强，跨国公司利润减少，因此在此时，B地区所需支付的额外补贴就越多。图1中实线与虚线的交点就是跨国公司决策的临界点，即Ω=0的点。图2说明了Ω与CM与Φ之间的关系。图2中，平面Ω=0以上的浅色三角形部分表示技术较落后B地区比技术较发达A地区愿意多支付的补贴额大于跨国公司在A地区比在B地区能够多获得的利润，在这种情况下，B地区将获得跨国公司的研发投资;同样，平面Ω=0以下的深色部分所代表的情况是A地区将获得跨国公司投资。

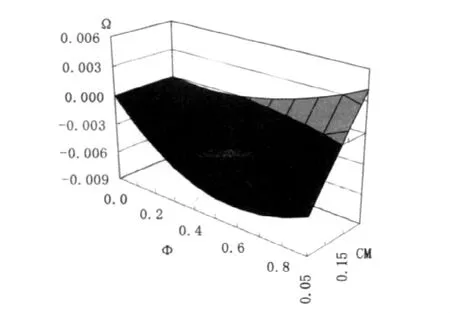
图2 跨国公司的投资判断指标图

从图2可以看出，随着CM增大，B地区争取到跨国公司投资所必须达到的最小技术溢出率在减小，B地区更容易获得跨国公司的选择投资。①① 通过计算，在两地初始成本相近且较大 (CA=0.25，CB=0.30，r=10)时，当CM=0.2，Φ＞0.36或者CM=0.15，Φ＞0.81时，Ω＞0，B地区将获得跨国公司投资;当CM=0.2，Φ＜0.36，CM=0.15，Φ＜0.81或者CM=0.1，0.05时，Ω＜0，A地区将获得跨国公司投资。

在考虑福利变化情况时，若不进行政府补贴，跨国公司将必定选择在A地区进行投资，因此我们选择此情况作为参照，即没有政府补贴、跨国公司投资A地区时A、B两地及整体福利作为基准值，来考察进行政府补贴、两地竞争后以上各福利的变化情况，可以得到图3。

图3中的ΔWA、ΔWB和ΔΣW即为在考虑政府补贴两地竞争跨国公司投资因素情况下与不考虑政府补贴跨国公司直接投资A地区情况下，A、B及两地整体各福利的差额。从图3中我们看到，与未考虑政府补贴因素 (跨国公司投资在A地区)的福利情况相比，在两地实施政府补贴竞争跨国公司投资后，不论最终竞争结果如何，两地的整体福利有所下降，在图3中反映为A、B两地区整体福利变化值Δ∑W为负。就两地区分别来看，不论跨国公司最终是否选择投资A地区，A地区都将在竞争中受损;而当跨国公司选择投资B地区时，B地区将从中受益，而当跨国公司选择投资A地区时，B地区福利不受影响。这一点也符合上述命题三的结论。②像这样的模拟，还有两种情况:两地成本相近且较低与两地成本差距较大。若需要这样的分析，可与作者联系取得。

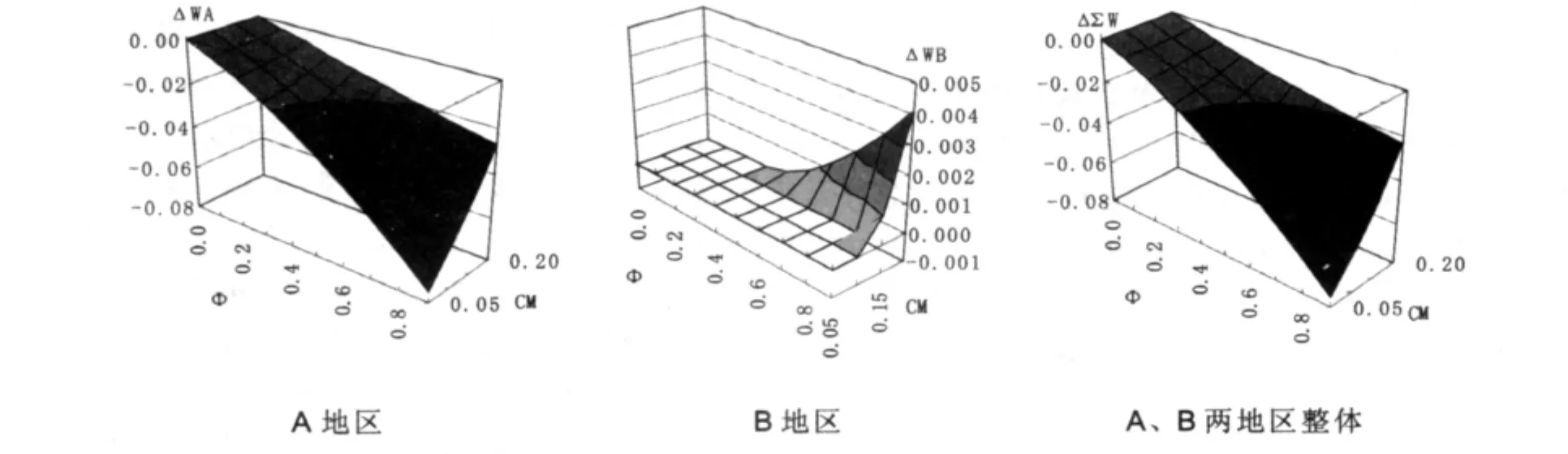
图3 A、B两地及整体福利变化情况 (CA=0.25，CB=0.30)

(二)研发效率r不同的情况

研发效率参数r越大，说明达到相同的研发成果 (即成本缩小额X)所需支付的研发投入越大，研发效率越低下;反之，研发效率越高。假定两地企业和跨国公司初始成本都固定，分别是CA=0.15，CB=0.20，CM=0.1，Φ∈ (0，1)，考察跨国公司的研发效率不同时的情况，r分别取3，7，11，15，我们可以得到图4。

从图4中可以看出，随着r增大 (研发效率降低)，技术落后地区B比A地区愿意多支付的补贴额MAXUB－MAXUA也会增大，但是增大幅度会随r的增大而减弱，在图4上就反映在虚线越往上越密集;同样，跨国公司在两地的利润差额ΔΠM也会减少，但是减小幅度也随r增大而减弱，图4上反映在实线越往下越密集。这是因为研发效率的降低使得跨国公司的研发热情减少，致使本模型中的成本缩小额减小，在此情况下，B地区由于初始成本较大，通过技术溢出获得的收益就会较多，但是随着研发效率的降低，成本缩小额减小的越来越慢，这样B地区比A地区的获益越来越少，反映在ΔΠM和MAXUBMAXUA的变化幅度减小。

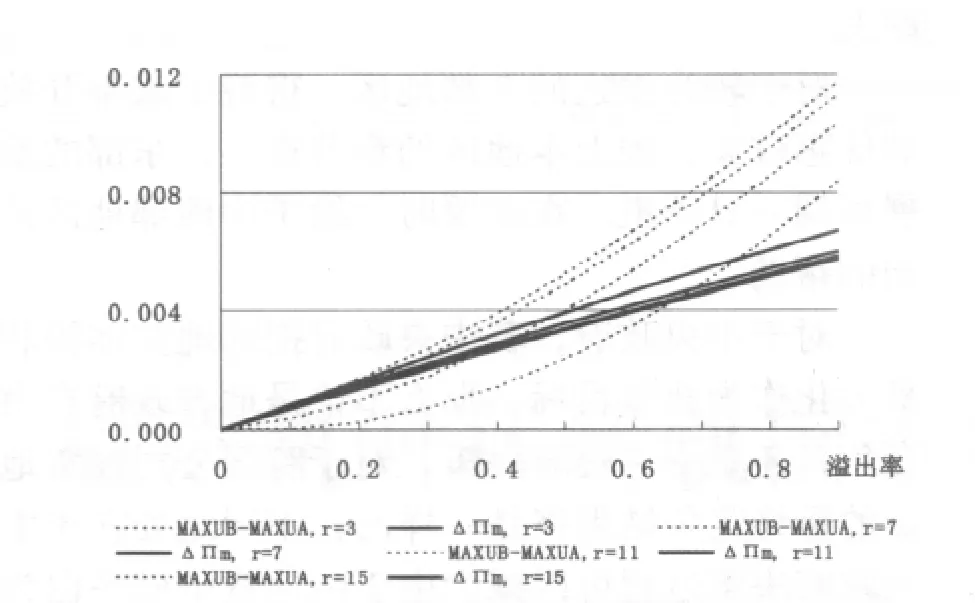
图4 两地福利差额与跨国公司利润差额关系图 (不同研发效率的情况)

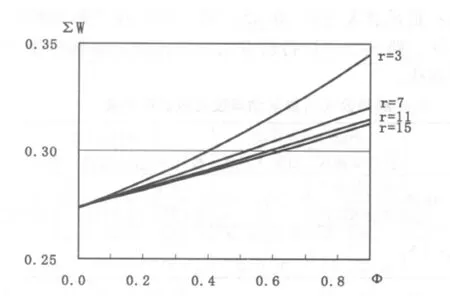
图5 两地整体福利水平与研发效率关系图

由此我们可以看到，跨国公司的研发效率越低下，对技术落后地区竞争跨国公司投资越有利。可是我们必须注意到，研发效率低下同时会对整个社会福利带来负面影响，从图5中我们可以很清楚地看到，随着研发效率的提高，两地区及整体社会福利都将随之增加。

(三)从事研发与否对选择投资地区的影响

跨国公司是否从事研发活动对其投资地的选择也会产生影响。在这种情况下，我们假定技术先进地区企业和跨国公司初始成本固定，分别是CA=0.12，CM=0.1，Φ∈ (0，1)，r=10，考察跨国公司的研发与否对跨国公司选择投资地影响情况，CB分别取0.15，0.2，0.25，0.3四种情况，我们可以得到图6。

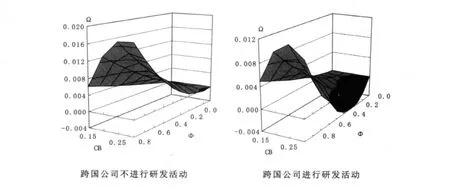
图6 跨国公司的投资判断指标图 (研发与否对比情况)

从图6中可以看到，在不进行研发活动时跨国公司投资B地区比投资A地区使得整体福利增加额，有所降低，在图6中表现为Ω曲面的整体下降，同时在一部分情况下，在跨国公司不进行研发活动时选择投资B地区，而当其进行研发活动后将改变为投资A地区，就竞争跨国公司投资而言，跨国公司进行研发活动将恶化技术较落后地区的竞争力，而对技术较先进地区有益。

例如，通过计算，我们可以得到表1结论。

对于福利变化问题，我们主要关心研发活动对A、B两地区以及整体福利的影响情况，因此，我们以跨国公司不进行研发活动为基准值来考察跨国公司进行研发活动后以上各福利的变化量，由计算可得，不论是技术较发达地区还是技术较落后地区，或是两地区整体，跨国公司从事研发活动对其社会福利的影响并不必然为正。在A、B两地区技术水平差距较大，且技术外溢率较大 (Φ∈ (0.6，0.9))时，跨国公司从事研发活动会使社会福利恶化;技术外溢率较小 (Φ∈ (0.1，0.3))时，跨国公司从事研发活动可以使社会福利改善;在A、B两地区技术水平差距不是足够大 (CB＜0.25)时，不论技术外溢率如何，跨国公司进行研发活动都将使两地整体福利恶化。

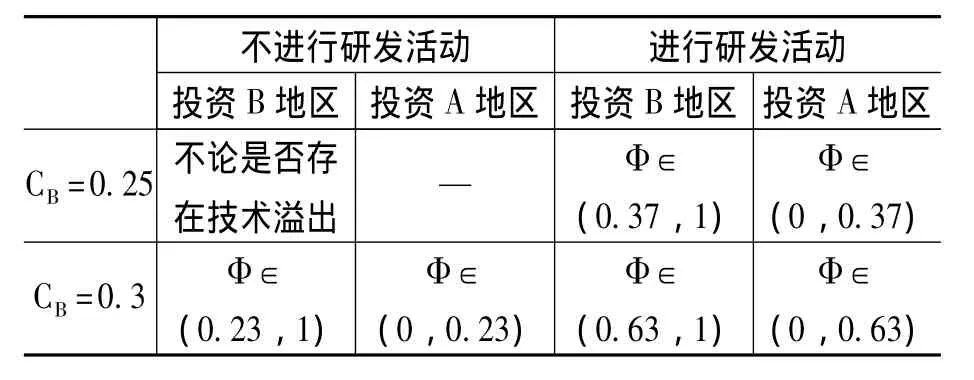
表1跨国公司研发活动与投资地选择比较

五、结 论

本文拓展了BC两地区竞争FDI三方博弈的模型，引入成本缩小型的研发变量，将两种现实情况统一到一个分析框架之内。通过建立动态博弈模型说明补贴政策、研发活动、技术溢出率等变量对跨国公司投资地选择和两国福利水平影响。

通过模型推导和模拟分析，我们得到在跨国公司从事研发活动且存在技术外溢条件下，在两地技术水平有差异情况下，两地间不进行竞争，则跨国公司必然选择技术较先进地区投资;两地间给予跨国公司投资补贴的竞争在一定条件下可以改变跨国公司的选择;与不进行研发活动相比，跨国公司进行研发活动，对技术较落后地区竞争外商直接投资有不利影响，并且也不必然会使两地福利水平增加，不过研发效率的增加会帮助提升两地整体福利水平。

若中央政府把两地整体福利最大化作为政策目标，那么不论是地方政府自由竞争，还是中央政府决策，最终的竞争结果将是一样的，不同之处在于中央政府决策过程可以减少由于竞争两地区一味增加的补贴额。

在当前的发展形势下，我国各地区政府一方面强调招商引资，一方面强调研发与学习。但是，我国区域禀赋与发展迥异，怎样在激烈的竞争环境下，保证统筹区域协调发展，是中央政府与各地方政府所深思的话题。

对于技术落后地区，我们可以看到在对跨国公司从事研发活动的投资的竞争中该地区更不占优。那么该地区就要努力增进技术学习能力，扩大对技术溢出的吸收能力，增强竞争能力 (技术溢出率Φ越大，对相对较落后地区的引资竞争越有利)。另一方面，要积极接受来自东部地区的产业转移，但不能盲目地接受低水平和高污染的产业，并且与此同时人才、配套产业也应该跟上。

对于较为发达的东部地区，得益于改革开放的优惠政策，加上本地区的艰苦奋斗，东部的发展可谓一日千里。在必要时，给予中西部地区适当的帮助。

对于中央政府，若中央政府把两地整体福利最大化作为政策目标，那么不论是地方政府自由竞争，还是中央政府决策，对于跨国公司投资地点的最终竞争结果将是一样的，不同之处在于中央政府决策过程可以减少由于两地竞争而平白为跨国公司增加的补贴额。所以中央政府要权衡好这样的竞争，在适当的时候对中西部地区实行政策倾斜，以减轻其在跨国公司研发投资的竞争中的不利局面，避免因技术差距越来越大的恶性循环造成的地区间发展失衡，统筹区域协调发展。

［1］Tiebout，C.M.A Pure Theory of Local Expenditures［J］.The Journal of Political Economy，1956，64(5).

［2］Haufler， A.， Wooton，I.Country Size and Tax Competition for Foreign Direct Investment［J］.Journal of Public Economics，1999，71(1):121－139.

［3］Barros，P.，Cabral，L.Competing for Foreign Direct Investment［J］.Review of International Economics，2008，(8):360－371.

［4］Fumagalli，C.On the Welfare Effects of Competition for Foreign Direct Investment［J］.European Economic Review，2003，(47):963－983.

［5］岳中刚.地区间竞争外商直接投资的福利效应分析［J］. 产业经济研究，2005，(1):17－23.

［6］Kuemmerle，W.Building Effective R＆D Capabilities abroad［J］.Harvard Business Review，1997，(2).

［7］Kumarz，N.Determinants of Location of Overseas R＆D Activity of Multinational Enterprises:The Case of US and Japanese Corporations ［J］.Research Policy，2001，30(1):159－174.

［8］Fors，G.，Zejan，M.Overseas R＆D by Multinationals in Foreign Centers of Excellence［D］.Stockholm School of Economics working Paper，1996.

［9］郑京淑.跨国公司海外研发机构的区位研究［J］.世界地理研究，2000，(1):10－16.

［10］喻世友，万欣荣，史卫.论跨国公司R＆D投资的国别选择［J］. 管理世界，2004，(1):46－54.

(责任编辑:于振荣)