改进偏最小二乘回归在电力负荷预测中的应用

季泽宇，袁 越，邹文仲

（河海大学 能源与电气学院，南京 210098）

中长期电力负荷预测通常通过以往的数据找出负荷的变化规律，从而分析负荷未来的变化趋势［1—3］。这类方法主要有：回归分析法、时间序列法、灰色预测法以及组合预测方法等［4—7］。其中，应用最小二乘法的一般多元线性回归方法简单有效，被广泛采用。但是在实际电力负荷分析过程中，由于自变量往往存在多重相关性且有时样本容量较小，可能会造成回归分析式不合实际而使预测误差偏大，为此，偏最小二乘法得到了应用［8］。

在一般的偏最小二乘法中，所有自变量都被保留，可以反映各个变量间的关系，但是，这一性质并不一定能提高负荷预测结果的准确度，无用的自变量反而可能会引入误差。由于传统最小二乘的参数筛选方法往往基于数据总体符合线性正态分布误差的模型假设，在更为复杂的偏最小二乘中无法应用，所以，可以用非参数统计方法Bootstrap来解决此类问题。Bootstrap是一种基于数据模拟的统计方法，由美国斯坦福大学教授Efron于1979年提出［9—10］，应用在偏最小二乘法的变量检验中可以去除非显著变量因素，使模型更为简洁、变量作用关系更为明确，同时预测精度得到提高。

本文使用偏最小二乘回归预测中长期电力负荷，并针对其不足采用Bootstrap方法对回归表达式中变量做出筛选。结果表明，经过这种改进后，电力负荷预测结果更加准确，同时回归表达式中负荷数据与其影响因素之间的关系也更为清晰。

1 偏最小二乘回归模型及Bootstrap检验方法

1.1 偏最小二乘算法

电力负荷预测中，因变量只有电力负荷，只需采用多自变量与单因变量的偏最小二乘简化算法［11—12］。设自变量x数目为m，因变量y数目为1，统计的样本数（年数）为n，由此构成统计数据表X=（x1，x2，…，xm）n×m，Y=（y）n×1。

从X中提取主成分th，h=1，2，…，k，使之能够满足：①th包含原数据X变异信息尽可能最大；②th对Y有很好的解释能力；③th加入后方程的预测能力有明显改善。

提取的主成分之间相互独立，且与因变量Y存在明显的相关关系。分别作X、Y对th的回归，而Y则可以表示为X的回归形式，由此得出自变量与因变量之间的关系。从X中连续提取k个主成分th，直到回归方程达到一个满意的精度，同时保证样本扰动误差尽量小。这样计算可以有效解决自变量的多重线性关系，得到比较准确的偏最小二乘回归表达式。

1.2 偏最小二乘法计算过程

（1）数据标准化处理

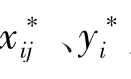
（2）提取主成分th

式中：wh是Eh的一个轴，为单位向量，且有‖wh‖2=1。

为使t1能尽量多的代表E0中的变异信息，根据优化方法，求解得

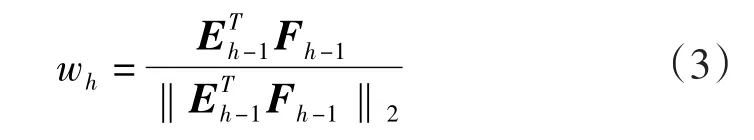
然后实施Eh以及Fh在th上的回归

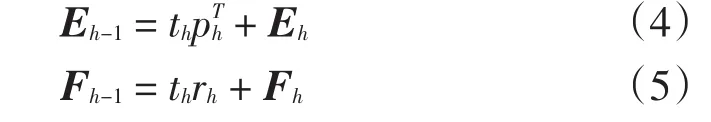
式中：Eh、Fh为残差矩阵；ph、rh为回归系数，并且满足

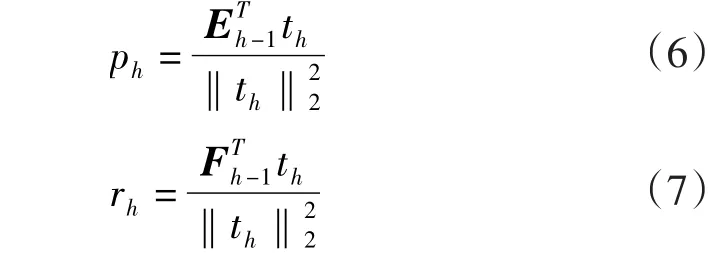
由式（4）可以得到提取主成分后的残差

由式（8）、式（2）可以将th改写为E0的线性组合

（3）交叉有效性检验

每次新成分th都需检验其是否对方程的预测能力有明显改进，以决定到底是否引入该成分。

设h个成分拟合后，第i个值y*i的拟合值为设去除样本i，利用剩余的样本提取h个成分回归计算得到的表达式，预测出y*i的值为ˆy*h（-i） 。定义

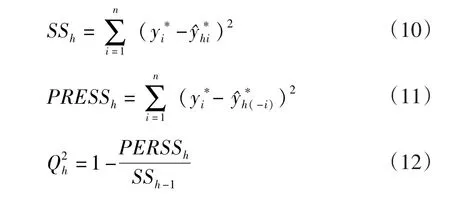
当Q2h≥0.097 5时，则认为成分th对于预测能力的贡献是显著的，在表达式中引入这个成分，否则认为其带来过多样本点的扰动误差，th被舍弃，同时停止主成分的提取。

（4）建立回归表达式

重复步骤（2）、（3）连续提取成分th，并且每次对其进行交叉有效性检验，直到th不满足检验条件，进入下一步骤。

若此时共提取k个主成分，则F0的回归方程

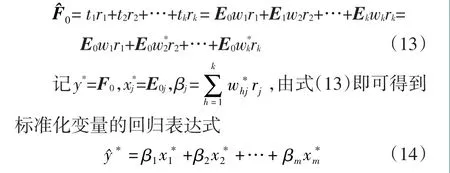
根据式（1）进行变量标准化逆过程，得到原始值的回归方程

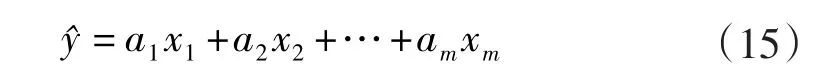
1.3 Bootstrap原理

由于式（15）中模型参数的估计量具有非常复杂的非线性性质，很难得到其在原假设下的精确分布，无法确定其参数的临界值［13］。Bootstrap可以有效解决这个问题，它通过原始数据中有放回地随机抽取一定数量的观测值，组成一个新样本，计算出相应参数值。经过这样的反复抽样，在大量实验下就可以得到反映这个数据集合的参数总体分布了。根据参数的这种分布可以得到在一定检验标准下参数的临界值，对参数作检验，进而进行取舍。

1.4 Bootstrap参数检验过程

通过偏最小二乘计算得到式（15）后，对各个自变量参数进行检验，去除影响不显著的因素。具体步骤如下：

（1）建立Bootstrap样本

在初始数据中用蒙特卡洛方法随机产生一个与原始样本类似的样本。抽样时，每次记录一组数值后都再放回数据表。如此记录nB（nB＜n）组数据，得到的新样本即为Bootstrap样本，样本容量为nB。

（2）样本回归

以得到的Bootstrap样本做偏最小二乘回归，成分数取原始数据回归所用成分数k，得到

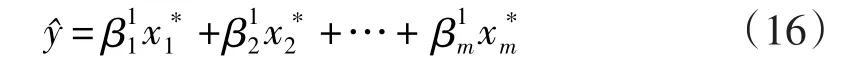
（3）重复取样

重复步骤（1）、（2）共B次（B取一个较大的数），得到B组系数

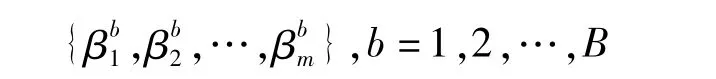
（4）计算临界值

（5）参数检验判断

如果|βi|＞ δi，则认为变量xi作用显著，否则认为xi作用不显著，未通过检验。

（6）重新进行回归计算

若自变量不显著，去掉此变量后更新原始数据，重新进行偏最小二乘回归计算，否则，结束回归分析，根据式（16）得到原始值回归方程。

2 算例分析一

2.1 原始数据

以江苏省2000—2009年农村用电量及相关因素的统计量为例［14］，分别运用一般最小二乘法、带变量筛选的逐步回归法、偏最小二乘法以及带变量筛选的Bootstrap检验偏最小二乘法对2000—2007年的数据进行分析，以2008、2009年的数据比较各种方法的预测精度。

表1为原始数据（此处只显示2位小数），其中：因变量为农村用电总量y；自变量为农村人口x1、农村家庭人均收入x2、第一产业总值x3、第二产业总值x4、第三产业总值x5、农林牧渔总产值x6、农作物播种面积x7。

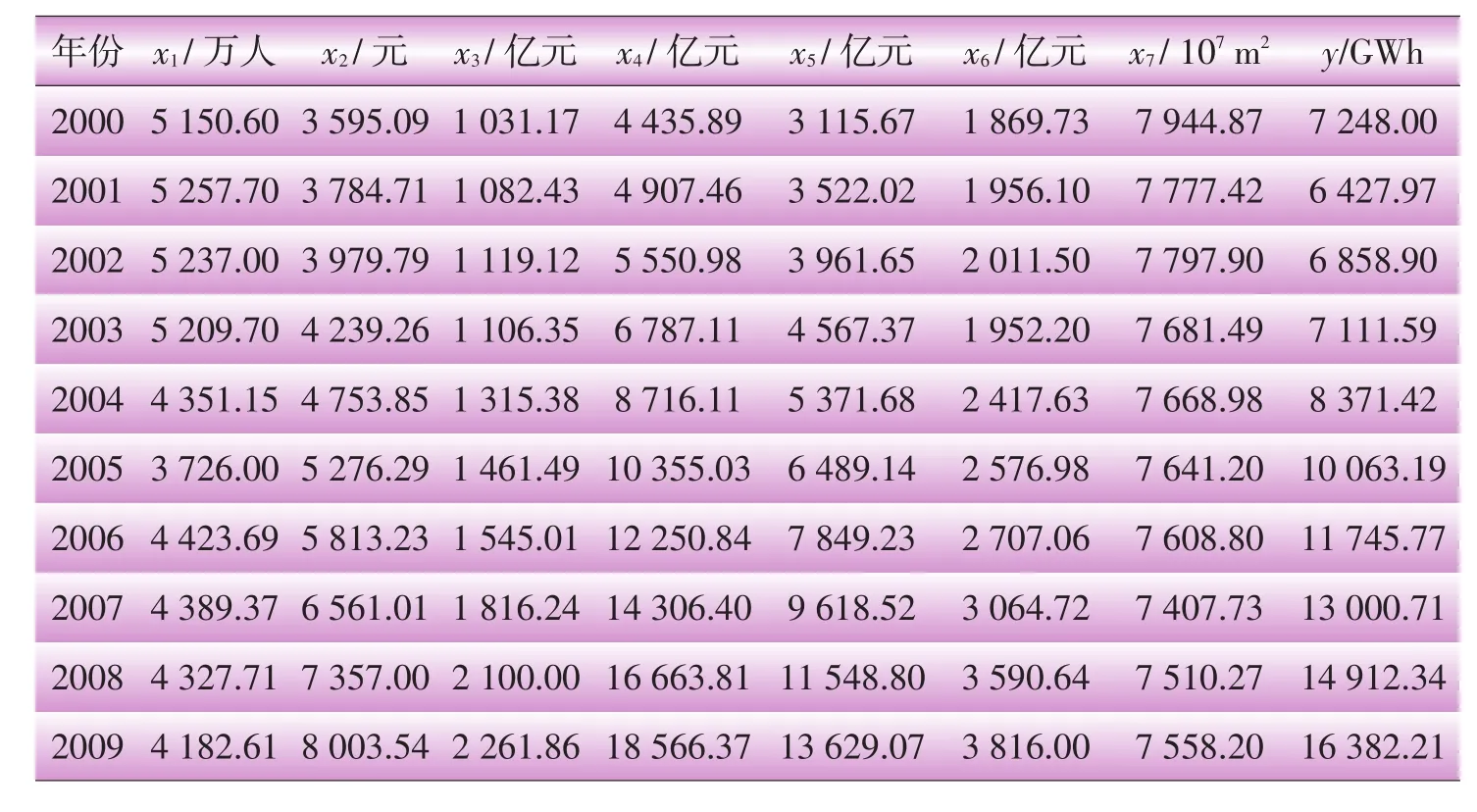
表1 江苏省2000—2009年农村用电量及其因素统计

对原始数据进行相关性分析，结果如表2所示。可以发现，各自变量间存在明显的相关性。本算例中，分析的样本数只有8个，而自变量多达7个，同时多重相关性严重，一般方法难以得到可靠的回归结果。下面通过偏最小二乘回归进行分析，计算在C++环境下实现。

2.2 偏最小二乘法分析

（1）提取成分t1，得

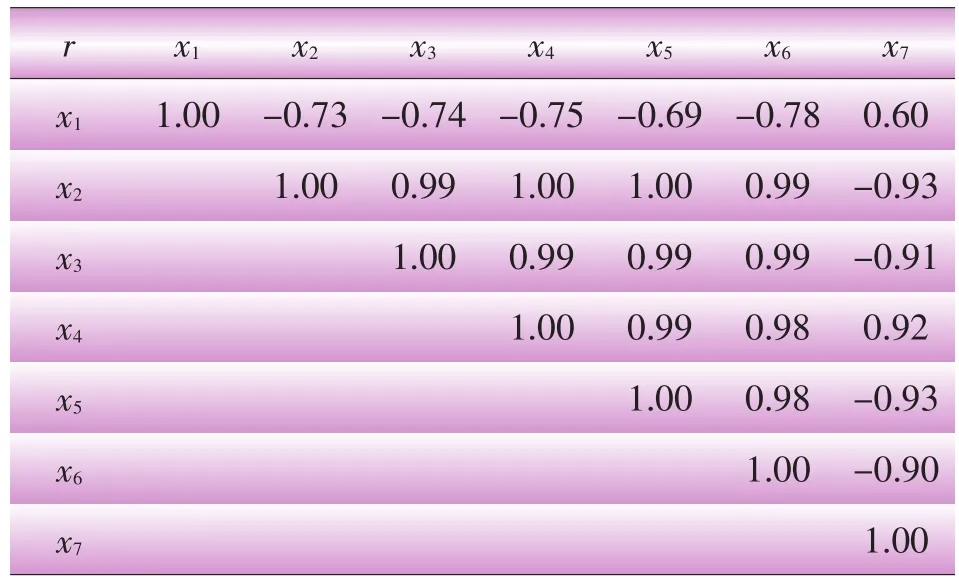
表2 各变量相关系数表

进行交叉有效性检验得Q2=0.908＞0.097 5，继续运算。

（2）提取成分t2，得

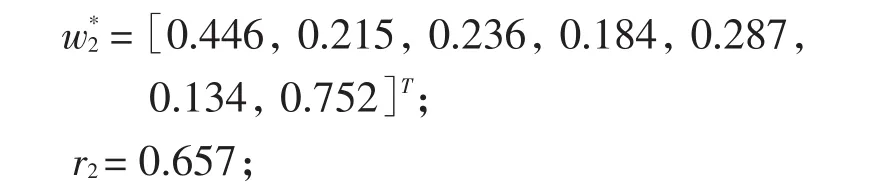
可决系数R2=0.984。

进行交叉有效性检验得Q2=0.114＞0.097 5，继续运算。

（3）提取成分t3，得

进行交叉有效性检验得Q2=-0.055＜0.097 5，停止运算。

（4）得出回归方程

由上述分析可知，提取2个成分已经足够，如式（17）所示。

经标准化逆过程，得到原始值回归方程

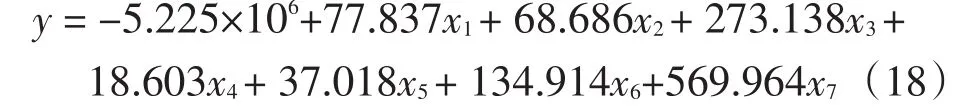
这个表达式就是一般偏最小二乘法的结果，式中各项系数都为正，基本反映了变量的现实关系。

2.3 基于Bootstrap筛选变量的偏最小二乘分析

分析式（18）中的参数是否作用显著：取Bootstrap样本1 000个（B=1 000），样本容量nB=7，按照检验水平α=0.1进行分析。计算相应系数集合｛˜βbi｝，元素排序后取第100（B×α）个元素作为临界值。每次实验临界值有一定变化，但不影响判断。α=0.1时，7个自变量标准值参数的Bootstrap检验结果如表3所示。

表3 7个自变量标准值参数的Bootstrap检验

由表3可知x1和x7没有通过检验。在原始数据中剔除x1、x7，用偏最小二乘法做y关于x2～x6的回归。

提取主成分t1，进行交叉有效性检验得Q2=0.944＞0.097 5。

提取主成分t2，进行交叉有效性检验得Q2=-1.513＜0.097 5。

所以这里只需提取一个主成分，得到

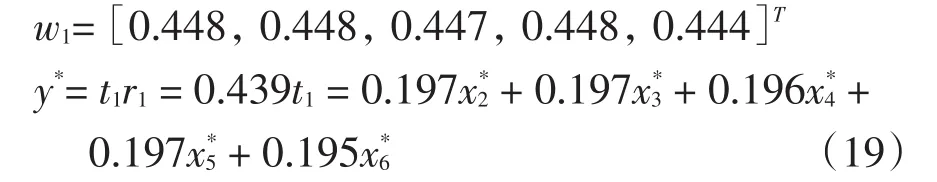
对于新的表达式，再次进行Bootstrap参数检验，B、nB、α取值与前一步相同，经过试验，得到临界值如表4所示。

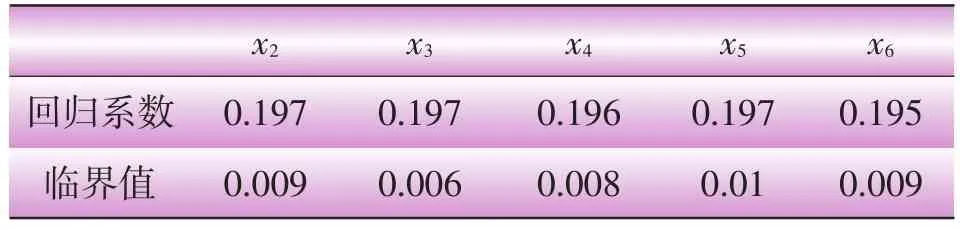
表4 5个自变量标准值参数的Bootstrap检验

所有参数都通过检验，化为原始值表达式

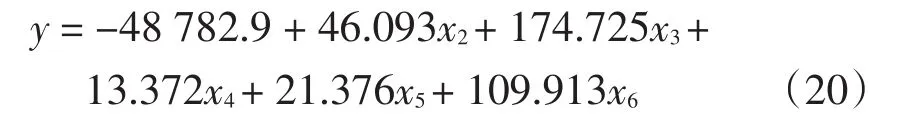
式（20）就是经过Bootstrap检验的偏最小二乘法最终结果。

2.4 算例结果

采用一般最小二乘法分析统计数据，得

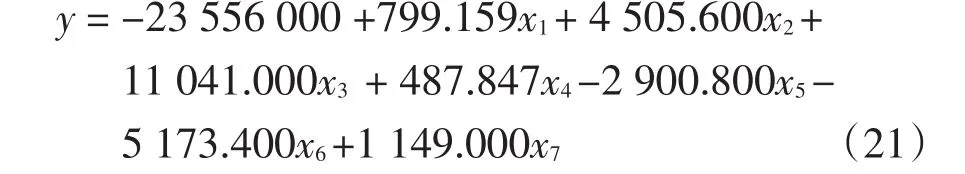
式中：自变量x5（省第三产业总值）和x6（农林牧渔总产值）前的系数为负，显然与事实不符。

采用逐步回归法，筛选自变量，进行最小二乘回归得

自变量只剩下x2（农村家庭人均收入）和x7（农作物播种面积），大量变量被去除，得不到变量间关系。

比较上述4种回归分析方法，数据的拟合与预测结果如表5、表6所示，图1为各方法对电量的拟合折线图。

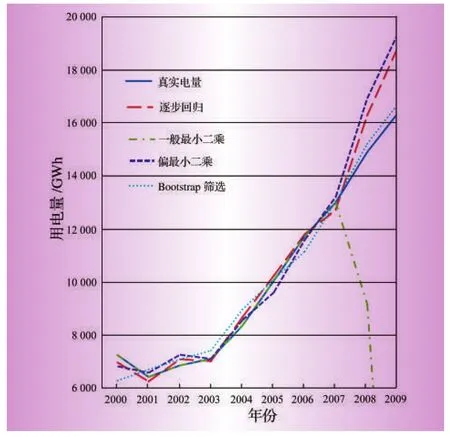
图1 各方法拟合预测结果比较

表5 历史数据拟合结果比较

表6 预测结果比较

综合分析表5、表6以及图1可以发现：一般最小二乘法的表达式实际意义不清晰，虽然在拟合阶段误差极小，但由于过分追求拟合，模型建立时大量吸收了各样本的扰动误差，在预测阶段效果极差；逐步回归法模型表达式变量比较少，实际变量的解释能力较弱，拟合和预测效果都处于中等；偏最小二乘法的表达式物理意义清晰，但在本算例中，预测效果并没有优于逐步回归法；经过Bootstrap参数检验的偏最小二乘法，由于去除了部分不显著的自变量，导致运算中可以从自变量中提取的主成份信息减少，致使拟合优度下降，但是，减少的不显著自变量同时也带走大量噪声，可提高数据间相关关系表述的准确性，使表达式物理意义更为清晰，有效提高预测准确度。

3 算例分析二

根据文献［12］中的算例（具体数据见文献），采用基于Bootstrap法的偏最小二乘法进行负荷预测分析，得到α=0.1时10个自变量标准值参数的Bootstrap检验结果，如表7所示。

表7 10个自变量标准值参数的Bootstrap检验

自变量x5和x10未能通过检验，去除这2个变量，得到新的偏最小二乘回归表达式

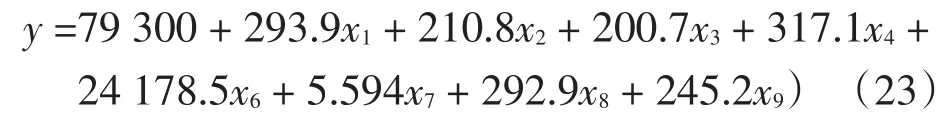
与原有方法的拟合、预测结果进行比较，如表8所示。

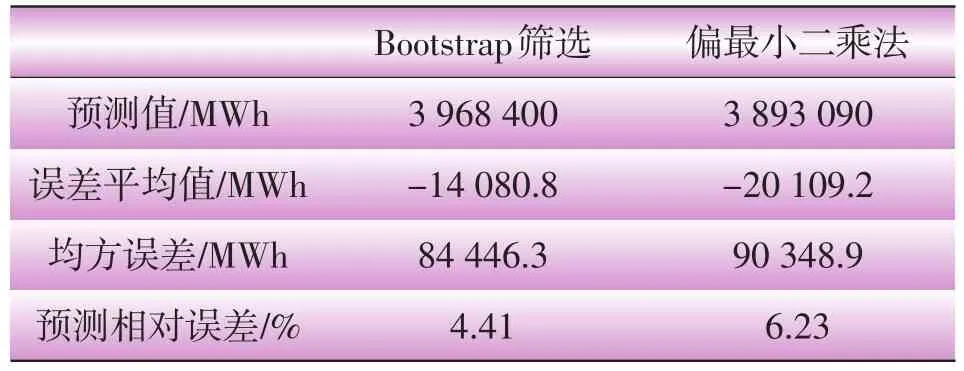
表8 拟合预测结果比较

从此算例可以看出：经过Bootstrap筛选后，回归计算结果无论在拟合程度还是预测准确度上都得到了提高。实际上，当采用多元回归方法进行负荷预测时，自变量越多，需要采集的数据也就越多。偏最小二乘法虽然在样本数量很少时仍能够得到较好的回归表达式，但是它并不能有效纠正采集大量数据时的统计错误，从而引入大量噪声。Boot-strap筛选自变量，可以把偏离较严重的自变量删除，进而得到更合理的结果。

4 结束语

电力负荷预测问题中，各变量经常存在多重线性关系。当存在数个自变量时，样本数量往往显得不够充足。偏最小二乘法吸收所有自变量，可以很好地反映实际物理意义，能够有效解决以上问题。然而，某些关系不显著或者数据存在问题的自变量会使表达式精度下降。

针对偏最小二乘回归方法在中长期电力负荷预测中的不足，提出基于Bootstrap筛选变量的改进算法，通过对2个算例的分析，验证了该改进算法的可行性，结果表明该改进算法得到的预测结果更加精确，具有一定的应用价值。

［1］ 康重庆，夏清，张伯明.电力系统负荷预测研究综述与发展方向的探讨［J］.电力系统自动化，2004，28（17）：1-11.

［2］ 罗治强，张焰，朱杰，等.中压配电网中长期负荷预测实践［J］.电力自动化设备，2003，23（3）：27-29.

［3］ Jia N X，Yokoyam R，Zhou Y C.A flexible long-term load forecasting approach based on new dynamic simulation theory — GSIM［J］.International Journal of Electrical Powerand Energy Systems，2001，23（7）：549-556.

［4］ 韦钢，贺静，张一尘.中长期电力负荷预测的盲数回归方法［J］.高电压技术，2005，31（2）：73-75.

［5］ 张庆宝，程浩忠，刘青山.基于最大熵原理的中长期负荷预测综合模型的研究［J］.继电器，2006，34（3），24-27.

［6］ 李翔，陈昊.基于时变参数模型的中长期负荷预测［J］.电力需求侧管理，2009，11（2）：32-34.

［7］ 吴耀华.基于GM-GRNN的电力系统长期负荷预测［J］.继电器，2007，35（6）：45-53.

［8］ 张恒喜，郭基联，朱家元，等.小样本多元数据分析方法及应用［M］.西安：西北工业大学出版社，2002.

［9］ Bradley Efron，TibshiraniR J.An introduction to the boot-strap［M］.BocaRaton ：Chapman and Hall/CRC，1994.

［10］ 王惠文，吴载斌，孟洁.偏最小二乘回归的线性与非线性方法［M］.北京：国防工业出版社，2006.

［11］ 王文圣，丁晶，赵玉龙，等.基于偏最小二乘回归的年用电量预测研究［J］.中国电机工程学报，2003，23（10）：17-21.

［12］ 毛李帆，江岳春，龙瑞华，等.基于偏最小二乘回归分析的中长期电力负荷预测［J］.电网技术，2008，32（19）：71-77.

［13］ 朱力行，许王莉.非参数蒙特卡洛检验及其应用［M］.北京：科学出版社，2008.

［14］ 中华人民共和国国家统计局.中国统计年鉴2009［M］.北京：中国统计出版社，2009.

［15］ 费宇，潘建新.线性混合效应模型影响分析［M］.北京：科学出版社，2005.

［16］ L沃塞曼.现代非参数统计［M］.北京：科学出版社，2008.