软岩巷道掘进支护方法研究

李凤，张成良，张鹏强

（1.昆明理工大学，昆明650093；2.东北大学，沈阳110819）

矿业是国民经济发展的支柱产业之一，而井巷掘进则是矿业发展最为基本的工艺环节，是保证矿山可持续发展的基础。近年来，井下巷道掘进遇到很多问题，其中软岩巷道的支护直接影响着矿山的开采，如何对软岩巷道进行合理的支护成为专家、学者研究和探讨的热点问题。

李琰庆等人提出在软岩中巷道掘进效率低并且变形大［1］，严重制约着矿山的可持续发展和生产能力的提高，同时也容易引发生产安全事故，因其支护费用升高、返修工程量大而成为矿山建设和发展的卡脖子工程［2－6］。

1 工程概况

塘子凹矿区1725巷道工程地质条件比较复杂，岩体的类型主要以风化、膨胀花岗岩和大理岩为主，花岗岩的变形主要表现为围岩内挤、开裂、散体冒落、片落、岩块体脱离等形式。其中，围岩内挤、开裂为主要变形和破坏形式。为了了解花岗岩巷道变形特征，主要研究巷道开挖后及支护后两阶段巷道的稳定性。

2 花岗岩巷道变形的数值分析

2.1 巷道稳定性的分析方法

为了研究花岗岩巷道在开挖后和支护后围岩的稳定性，通过数值模拟的方法，分析、计算花岗岩巷道掘进过程中围岩的应力、塑性区及安全率的分布情况，从而确定巷道最合理的支护方法，保证巷道的稳定性。

2.2 模拟采用的力学模型

在岩体破坏分析中，采用Drucker－Prager（D—P准则）［7］塑性破坏准则。此破坏准则考虑了静水压力对屈服与破坏的影响，特别适用于岩土类材料的本构模型。其屈服函数为：

式中：I1为应力第一不变量；J2为应力偏量第二不变量；p为材料塑性函数；q为材料弹性函数；σσ为材料压应力；τσ为材料剪切应力；a、k为D－P准则材料常数，a、k的值取决于C、φ值，它们之间存在如下关系：

C、φ分别是材料黏聚力和内摩擦角，另外，材料在拉应力状态下，采用抗拉破坏强度准则。其力学模型为

式中：σt为材料所受拉应力；Rt为材料抗拉强度。

如果拉应力超过材料抗拉强度（F≥0），材料将发生抗拉破坏。

3 模型的建立与计算

3.1 力学参数的选取

通过前期的调查和室内试验确定了围岩的力学参数，并应用到围岩的稳定性分析中，实践证明所选用的力学参数是合理的。因此，模拟分析也采用这套力学参数，计算模拟中采用的力学参数见表1。

表1 模拟计算所采用的参数表Table 1 Parameters used in simulation

3.2 模型的建立和求解

根据巷道的开挖断面，结合岩石力学相关理论，建立三维有限元模型［8］。巷道断面为三心拱［9］，尺寸2.4m×2.6m。其模型大小为：50m×65m×60 m，即沿巷道方向取50m（z方向），垂直巷道方向取65m（x方向），铅垂方向取60m（y方向），由于1725中段距地表大约350m，巷道顶部为大理岩，利用高度与荷载的关系，对模型上部施加9.625 MPa的均布荷载。共计97 190个节点，22 680个单元节点。单元网格划分、计算机模拟巷道形态示意图分别见图1～2。

3.3 计算方案

本次模拟分三个步骤进行：1）巷道开挖后不进行任何加固；2）利用多方案对巷道顶板及两帮进行加固处理［10－13］；3）在步骤2的基础上对底板［14－15］进行加固处理，在分析时由于步骤3是在步骤2的基础上进行，所以在得出步骤2的较优方案后再对步骤3进行分析、模拟。

通过顶板及两帮采用1.5m和1.8m锚杆支护，喷射混凝土厚度5cm和10cm，间排距0.75m ×0.75m、0.75m×1.0m和0.75m×1.2m，将步骤2分为12种模拟方案［14］。

图1 三维有限元计算机模型网格划分图Fig.1 Map of three dimensional finite elements model

3.4 计算结果分析

3.4.1 原始巷道计算结果分析（开挖后的裸巷）

在模拟的第一步即对巷道进行开挖，从模拟结果可以看出，由于巷道处于风化、膨胀的花岗岩中，开挖后整体破坏都比较严重，特别是巷道的顶板和底板及两帮底部。应力主要集中在底板与两帮接触部位，最大压应力为–23.094MPa，巷道的安全率最小为0.75，整体塑性区比较明显，所以说巷道开挖后自稳能力很差，必须对其进行加固处理。

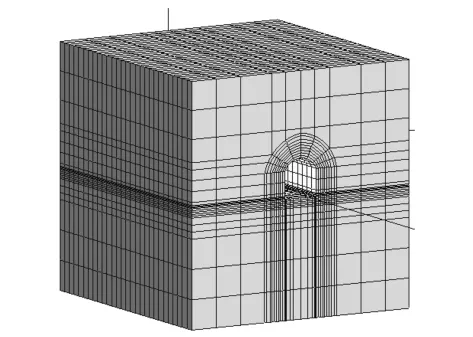
图2 模拟巷道开挖形态图Fig.2 Map of tunnel excavation simulation

3.4.2 对步骤2中的12种方案进行综合分析

经过对开挖后的裸巷进行分析，可以清楚地看到，巷道在无支护、加固的前提下是不可能自稳的，所以必须对巷道进行支护、加固处理。根据现场施工的顺序，先利用锚杆、钢丝网、喷射混凝土联合对顶板及两帮进行加固。锚杆及喷射混凝土层示意图见图3～4。由于锚杆长度、间排距、混凝土喷层厚度方案较多，这里仅给出一种方案示意图。

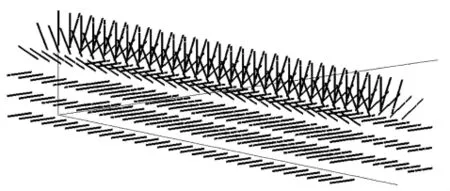
图3 锚杆支护加固模型图Fig.3 Map of bolting reinforcement model顶板、两帮锚杆间排距为0.75m×0.75m，长度为1.5m Roof，two－row spacing between the bolt in 0.75m×0.75m，length 1.5m

1）利用应力分布对12种支护方案进行分析

从模拟结果来看，12种支护方案最大压应力30.830MPa，最小为26.155MPa，相差4.6MPa；最大拉应力4.395MPa，最小为3.958MPa，相差不到0.4MPa。从应力分布图中可以看出，在锚杆间排距相同时，锚杆长度为1.8m、喷射混凝土厚度为10cm的方案应力要小于锚杆长度为1.5m、喷射混凝土厚度为5cm时的方案。

图4 喷射混凝土支护模型图Fig.4 Map of concrete support model顶板、两帮混凝土喷层厚度为5cm Roof，two side thickness of concrete sprayed 5cm

2）利用安全率分布对12种支护方案进行分析

首先，在锚杆长度厚度一定的前提下，喷射混凝土厚度为10cm时巷道的安全率要高于混凝土厚度为5cm的情况。而在锚杆长度和混凝土厚度都恒定的条件，锚杆的间排距大小与巷道的安全率大小有直接的关系：锚杆间排距越大，则安全率越小；反之则安全率越高。其次，在对巷道加固后，无论锚杆长度为1.5m还是1.8m，在喷射混凝土厚度为5 cm时，所有方案的安全率均小于1，所以在施工中建议喷射混凝土的厚度尽量达到10cm。当锚杆间排距为0.75m×1.2m时，喷射混凝土厚度达到10 cm，巷道的安全率仍然小于1。当锚杆长度为1.8 m时，间排距为0.75m×0.75m和0.75m×1.0m两种方案的安全率分别为1.1和1.094，满足安全需要，而间排距为0.75m×1.0m时成本相对较低，所以建议采用1.8m锚杆、间排距0.75m×1.0 m、喷射混凝土厚度为10cm方案联合支护巷道顶板及两帮。

3）利用塑性区分布对12种支护方案进行分析

模拟发现，采用5cm厚的喷射混凝土方案在支护后巷道仍然有大量的塑性区出现，特别是巷道顶板，塑性区连片的现象比较明显，这也说明了5cm厚的喷射混凝土不能满足安全需要，而其它方案塑性区分布相差不大，很难判断出较优方案。

结合以上应力、安全率、塑性区各方面考虑，得出顶板及两帮采用1.8m锚杆支护，喷射混凝土厚度10cm，间排距0.75m×1.0m是较为合理的施工方案。

3.4.3 在步骤2的基础上对底板进行加固分析

从步骤2的分析结果中得知，顶板及两帮采用1.8m锚杆支护，喷射混凝土厚度10cm，间排距0.75m×1.0m是支护、加固顶板及巷道两帮的理想方案，在此基础上，提出了两种方案对底板进行加固：1）底部锚杆＋平底浇灌底板联合支护底板（见图5）；2）底部锚杆＋反拱浇灌底板联合支护底板（见图6）。在浇灌过程中，厚度均为25cm。

图5 底部锚杆＋平底浇灌底板联合支护底板Fig.5 The combined support bottom with bottom bolt and flat bottom pouring

图6 底部锚杆＋反拱浇灌底板联合支护底板Fig.6 The combined support bottom with bottom bolt and reversed arch pouring

模拟结果表明，在对底板进行平底浇灌后，底板最大压应力为26.325MPa，最大拉应力为4.128 MPa，进行反拱浇灌后分别是26.773MPa和4.050 MPa，平底浇灌和反拱浇灌时的安全率分别是0.688和1.241，两方案应力差异较小，而安全率相差较大，从塑性区的分布也可以清楚地看到，利用反拱浇灌后底板的塑性区明显地减少，所以论证了反拱浇灌较底板有较大的优越性。

4 结论

综合以上分析，可得到如下结论：

1）采用三维有限元软件对塘子凹1725中段软岩巷道支护进行了多方案模拟分析，所得结论和实际情况比较吻合，可以用模拟结果指导今后的施工。

2）从所采用的几种方案模拟结果来看，在利用喷锚网对巷道顶板、两帮进行支护时，锚杆长度为1.8m，间排距为0.75m×1.0m，喷射混凝土厚度为10cm是比较经济、合理的施工方案；在对底板进行加固时，利用锚杆支护的基础上，应采用反拱形式浇灌底板。

3）本次模拟还对锚杆在支护过程中的作用［16］进行了分析，结果表明，采用锚杆支护，不仅可以改善围岩的应力状况，抑制顶板围岩的变形和减小塑性区的范围，而且可以增强顶板的安全指数，提高围岩自承能力。因此，锚杆支护是一项整体效果良好、作用明显的控顶措施，也是保证生产安全的一种有效方法。

［1］ 李琰庆，陈同虎，宋友良，等.深部高应力软岩巷道支护技术优化及工程实践［J］.煤矿支护，2009（1）：23－27.

［2］ 薛顺勋，聂光国，姜光杰，等.软岩巷道支护技术指南［M］.北京：煤炭工业出版社，2002.

［3］ 李明远，王连国.软岩巷道锚注支护理论与实践［M］.北京：煤炭工业出版社，2001.

［4］ 李国富.高应力软岩巷道变形破坏机理与控制技术研究［J］.矿山压力与顶板管理，2003（2）：50－52.

［5］ 易丽萍.现代隧道设计与施工［M］.北京：中国铁道出版社，1995.

［6］ 朱维申.节理岩体破坏机理和锚固效应及工程应用［M］.北京：科学出版社，2002.

［7］ 谢文兵，陈晓祥，郑百生.采矿工程问题数值模拟研究与分析［M］.徐州：中国矿业大学出版社，2005.

［8］ 李绍才.三维有限元在巷道中的模拟研究［D］.昆明：昆明理工大学，2003.

［9］ 周昌达.井巷工程［M］.北京：冶金工业出版社，1994.

［10］ 周新贞.软岩巷道支护实践［J］.煤矿支护，2006（3）：38－39.

［11］ 岳国均，郭 瑞.软岩巷道支护技术的应用［J］.现代矿业，2010（8）：110－112.

［12］ 张红卫，李更新，户春峰，等.高应力软岩巷道支护研究［J］.矿业论坛，2010（15）：749.

［13］ 张朝阳.软岩巷道支护的探索实践［J］.煤炭技术，2002，28（2）：52－53.

［14］ 刘新河，田灵涛，陈 龙，等.薛村矿高应力软岩巷道支护数值模拟研究［J］.中国煤炭，2009，35（3）：55－60.

［15］ 潘一山.有限元数值分析方法分析巷道底臌问题［C］／／第一届中苏采矿学术交流会论文集.泰安：山东矿业学院，1991.

［16］ 陆家梁.软岩巷道支护技术［M］.长春：吉林科学技术出版社，l995.