基于虚拟脉冲响应函数与神经网络的结构损伤定位研究

张启亮，刁延松，佟显能，于 菲

(1.青岛理工大学土木工程学院，山东青岛266033;2.青岛同圆建筑设计有限公司，山东青岛266000)

基于振动测试的结构损伤定位方法一般是由结构的振动响应来提取结构的损伤特征参数，再根据结构的损伤特征参数来判断结构的损伤状况，故结构的损伤特征参数的选取直接关系到损伤定位结果的优劣。常用的结构特征参数有固有频率、模态振型及模态阻尼等模态参数。近年来，模态参数因其直接反映结构的状况而备受关注。但是模态参数受环境(如温度、湿度等)、工况及结构本身不确定性的影响很大，故基于模态参数的方法应用在工程实际中的很少。目前，已有学者陆续提出了一些非模态特征参数，如Biswajit［1］利用小波系数研究了双线性结构与迟滞系统的刚度衰减及损伤定位问题;Law［2］等通过小波包方法计算了结构的小波包能量及其分布以此检测定位损伤;Nichols［3］等人比较了吸引子维数和关联维数识别损伤的结果，得出前者比后者更准确的结论;Rutolo［4］等人将不同工况下的频率响应组成Hankle矩阵，奇异值分解法计算矩阵的秩后，根据秩的不同判断结构是否发生变化等等。这些方法都是以人工激励作为输入的。然而像跨海大桥、海洋平台等大型土木工程结构其结构复杂、体积庞大、造价昂贵，所处的环境恶劣，人工激励难以施加并且费用较高，环境荷载激励难以测试。针对这种情况，本文直接利用白噪声激励下结构两点响应构造虚拟脉冲响应函数，并对虚拟脉冲响应函数的幅值进行了小波包分解并计算其节点能量，以结构损伤前后的小波包节点能量变化量作为损伤特征向量，利用BP神经网络的模式分类功能进行结构损伤定位研究。海洋平台结构单损伤和多损伤的数值模拟结果表明，当结构损伤程度较大时，该方法是可行的并且具有较强的噪声鲁棒性。

1 基本理论

1.1 虚拟脉冲响应函数的获取［5］

现实中的大型土木工程结构如跨海大桥和海洋平台等所受的环境激励往往难以测得，而对结构动力系统，其激励与响应之间的关系是通过系统本身所固有的动力特性——脉冲响应函数或频率响应函数来体现的。脉冲响应函数中包含了系统所有的动力特性参数。因此本文直接利用白噪声激励下结构两点响应构造虚拟脉冲响应函数。虚拟脉冲响应函数的基本思想是以参考点的动力响应作为虚拟激励，计算参考点的虚拟激励与其他测点响应之间的虚拟脉冲响应函数，用来表征结构动力系统的动力响应。其理论分析见文献［5］。为了便于叙述给出频率响应函数的公式:

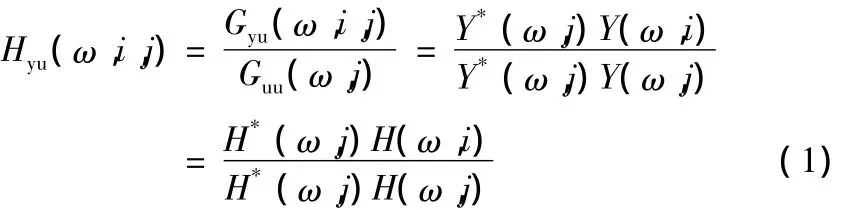
式中:Gyu(w，i，j)和 Guu(w，j)分别为参考点 j的响应(虚拟激励)xj(t)和测点i的响应xi(t)的互谱密度以及虚拟激励xj(t)的自谱密度;Y(w)为响应的傅里叶变换;Y(w，i)和Y(w，j)分别是响应xi(t)和虚拟激励xj(t)的傅里叶变换;Y*(w，j)是 Y(w，j)的复共轭;Hyu(w，i，j)、H(w)均为频率响应函数;H*(w，j)为H(w，j)的复共轭。

从公式中可以看出，两点响应的频率响应函数Hyu(w，i，j)能有效地消除激励频谱的影响，也就是说，对频率响应函数Hyu(w，i，j)进行逆傅里叶变换求得的虚拟脉冲响应函数可以有效地克服激励的随机性和不确定性，具有更好的激励鲁棒性，更好地反映了结构动力系统的动力特性。故可以将虚拟脉冲响应函数应用于结构的损伤定位。

1.2 虚拟脉冲响应函数的小波包分解

当结构系统的激励力向量一定时(假设忽略观测噪声)，结构损伤所引起的结构动力特性的变化，必定会引起不同小波包尺度(频带)上结构响应f(i，k)的变化，从而引起结构动力响应f(N，k)的能量在各个频带内的重新分布［5］。因此，结构动力响应f(N，k)在第i分解层的小波包能量谱向量Ei可以表示结构的损伤状态:

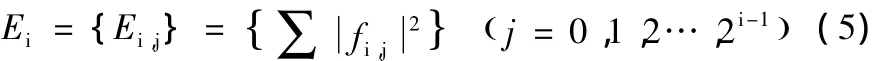
式中:fi，j表示第 i层分解节点(i，j)上的结构响应。

文献［6］论述了结构损伤前后小波包节点能量变化量比小波包节点能量对损伤位置更为敏感，本文以此为依据假设对白噪声激励下所得的虚拟脉冲响应函数f的幅值进行i层小波包分解，则虚拟脉冲响应函数f的幅值在第i分解层的小波包节点能量向量Ei可以表征结构的动力特性。

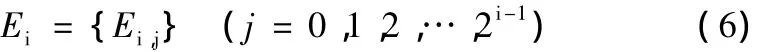
采用Db25小波作为结构损伤定位的小波函数，选用适宜的小波函数阶次和小波包分解层次对虚拟脉冲响应函数幅值进行小波包分解。将结构损伤前后小波包节点能量变化量作为结构损伤定位因子，对结构进行损伤定位。

小波包节点能量变化量为:

归一化的小波包节点能量变化量为:

1.3 BP神经网络

BP神经网络结构简单，算法容易实现，它最早被应用于结构的损伤识别中，也是目前应用最为广泛的人工神经网络模型。本文采用三层BP神经网络结构，即一个输入层、一个隐含层和一个输出层。理论证明三层的BP网络可以表示任意一个映射关系［7］。

BP神经网络的输入向量直接关系到网络识别效果，现采用如下方式构造输入向量。

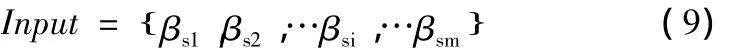
其中βsi(i=1，2，…，m)为归一化的结构损伤前后虚拟脉冲响应函数幅值第s层小波包分解第i个频带节点能量变化量。本文所用的神经网络的输出向量为:

其中Oi∈［0，1］。对于识别损伤位置的神经网络，Oi≈0.0表示i处没有损伤，而Oi≈1.0表示在i处有损伤。

1.4 基本步骤

第一步，获取虚拟脉冲响应函数。利用ANSYS10.0对海洋平台三维有限元模型进行时程反应分析获得节点加速度，然后利用MATLAB6.5编程获得虚拟脉冲响应函数。

第二步，获取损伤特征向量。利用MATLAB6.5对第一步获得的虚拟脉冲响应函数进行小波包分解获得节点能量，然后提取结构损伤前后节点能量变化量作为损伤定位特征向量。

第三步，将损伤定位特征向量作为BP神经网络的输入进行网络训练，最后将测试样本输入训练好的网络进行损伤定位。

2 数值模拟

2.1 有限元模型

本文利用ANSYS10.0建立如图1所示的海洋平台结构的三维有限元模型。基本参数如下:弹性模量为E=2.07×1011N/m2，密度为7 800 kg/m3，柱、横梁和支撑采用 BEAM4单元，顶板采用SHELL63单元，顶板上堆积质量采用MASS21单元进行模拟。该模型共有32个结点，50个BEAM4单元，1个SHELL63单元，4个MASS21单元。利用ANSYS10.0的时程反应分析模块进行时程反应分析，获得完好结构和损伤结构时的加速度响应信号，激励采用白噪声，沿Y向作用于二层结点9和10，采样频率是50 Hz，输出加速度响应信号的采样频率是50 Hz，选取四层结点2和二层结点10的Y向50 s内的加速度响应作为研究信号。

各种损伤工况均采用单元弹性模量折减来实现，单元编号如图1所示，模拟的损伤工况如表1所示。

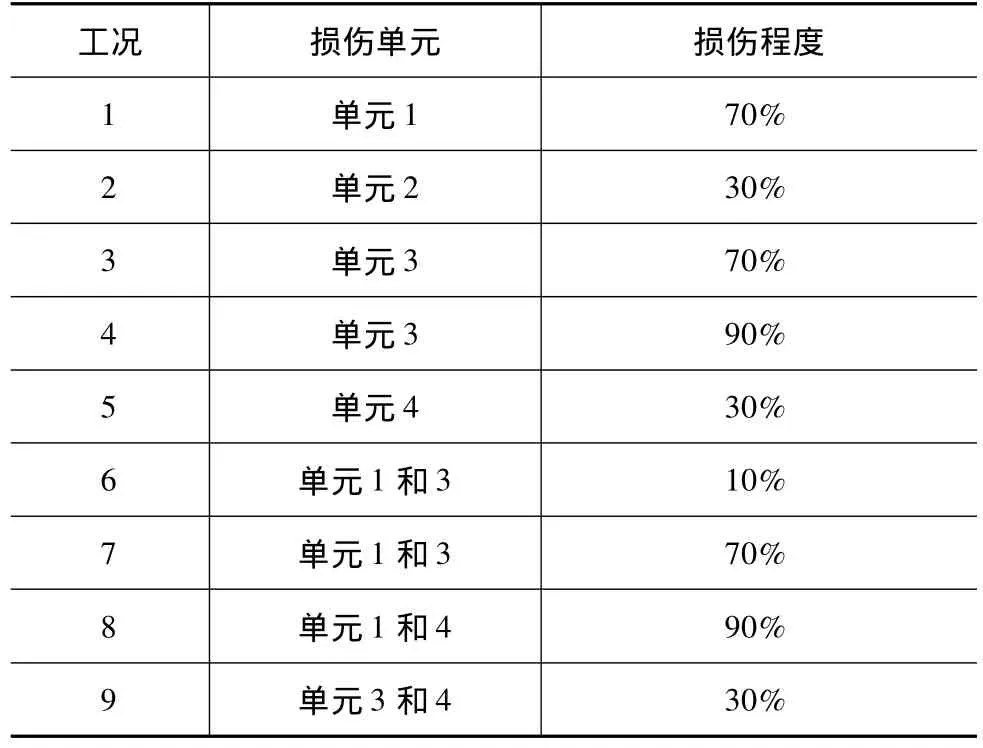
表1 损伤工况

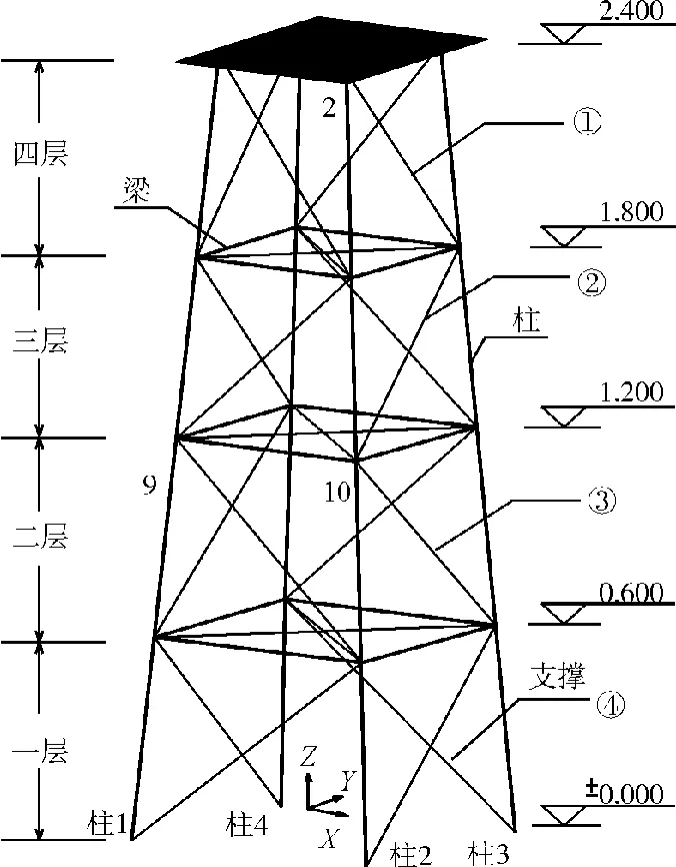
图1 数值分析模型

2.2 BP神经网络的训练与测试

以节点10的加速度响应作为虚拟激励，计算完好结构和损伤结构的节点2的频率响应函数，在此基础上采用逆傅里叶变换得到节点2的虚拟脉冲响应函数。对虚拟脉冲响应函数的幅值进行小波包分解，小波包分解时采用Db25小波函数，分解层次取为5。求得完好结构和损伤结构的节点能量值，进而求得结构损伤前后节点能量变化量。分别对单损伤和多损伤(这里单指两处损伤)的损伤工况进行了研究，采用结构损伤50%前后节点能量变化量作为网络训练样本。训练函数采用TRANLM，学习函数采LEARNGDM。网络训练样本和测试样本如表2和表3所示。

表2 单损伤的训练和测试样本

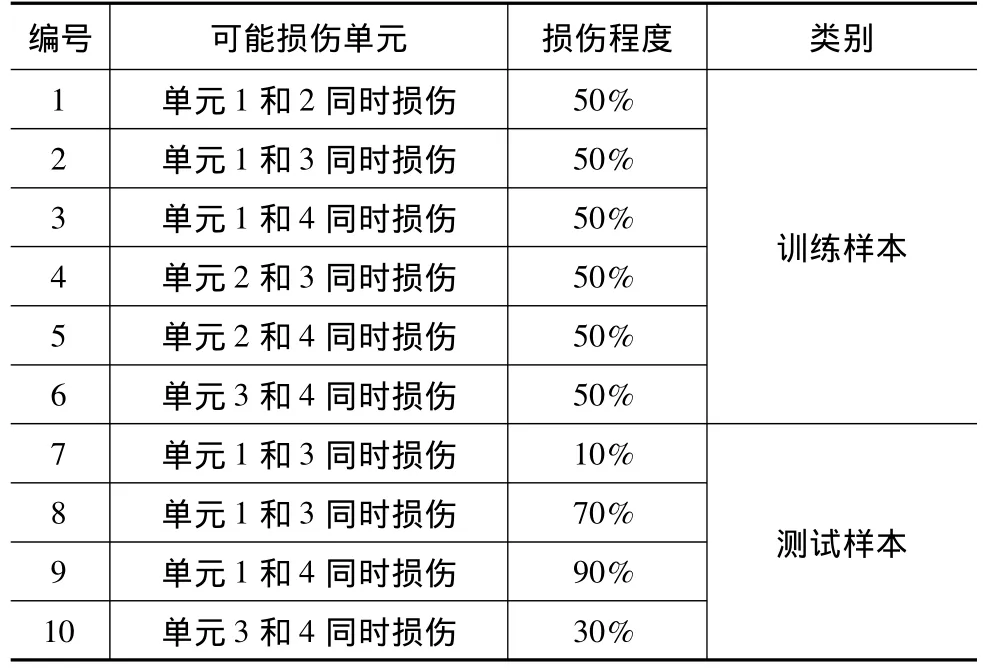
表3 多损伤的训练和测试样本

单损伤的网络结构为:32×10×4;训练参数为:最大训练次数500;训练精度1e－5;学习率0.05;显示训练迭代过程25;动量因子0.9。多损伤的网络结构为:32×13×4，训练参数为:最大训练次数1000;训练精度1e－5;学习率0.1;显示训练迭代过程50动量因子0.9。单损伤和多损伤的训练过程和测试结果如表4所示。

表4 单损伤和多损伤的网络训练过程和测试结果

从单损伤和多损伤的网络测试结果可以看出，该方法能准确地对发生不同程度的损伤结构进行损伤定位。

2.3 噪声鲁棒性分析

为考虑测量噪声的影响，在加速度信号中叠加了不同程度的正态分布的随机白噪声，噪声的模拟公式为:

式中:γi和分别为无噪声和有噪声时的加速度信号;εi为正态分布的随机数(均值为零，均方值为1);p是在测试样本上所加噪声的大小，本文取1%和3%。

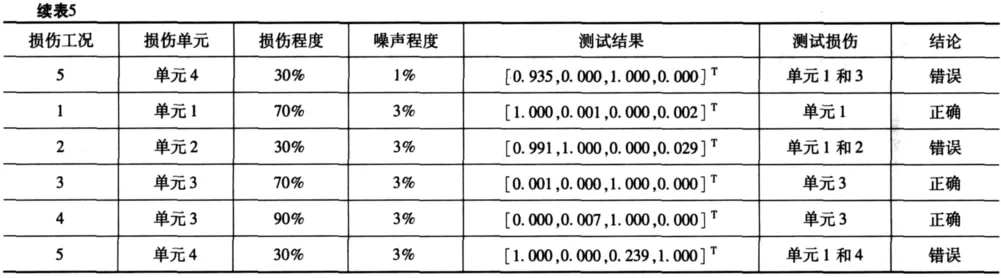
单处损伤时，加入1%噪声后的网络结构为:32×12×4，训练参数:最大训练次数100;训练精度1e－5;学习率0.1;显示训练迭代过程25;动量因子0.9。加入3%噪声后的网络结构为:32×11×4，训练参数:最大训练次数100;训练精度1e－5;学习率0.04;显示训练迭代过程25;动量因子0.9。训练过程和测试结果如表5所示。

?

?

多处损伤时，加入1%噪声后的网络结构为:32×13×4，训练参数:最大训练次数1000;训练精度1e－5;学习率0.005;显示训练迭代过程50;动量因子0.9。加入3%噪声后的网络结构为:32×11×4，训练参数:最大训练次数1000;训练精度1e－5;学习率0.008;显示训练迭代过程50;动量因子0.9。训练过程和测试结果如表6所示。

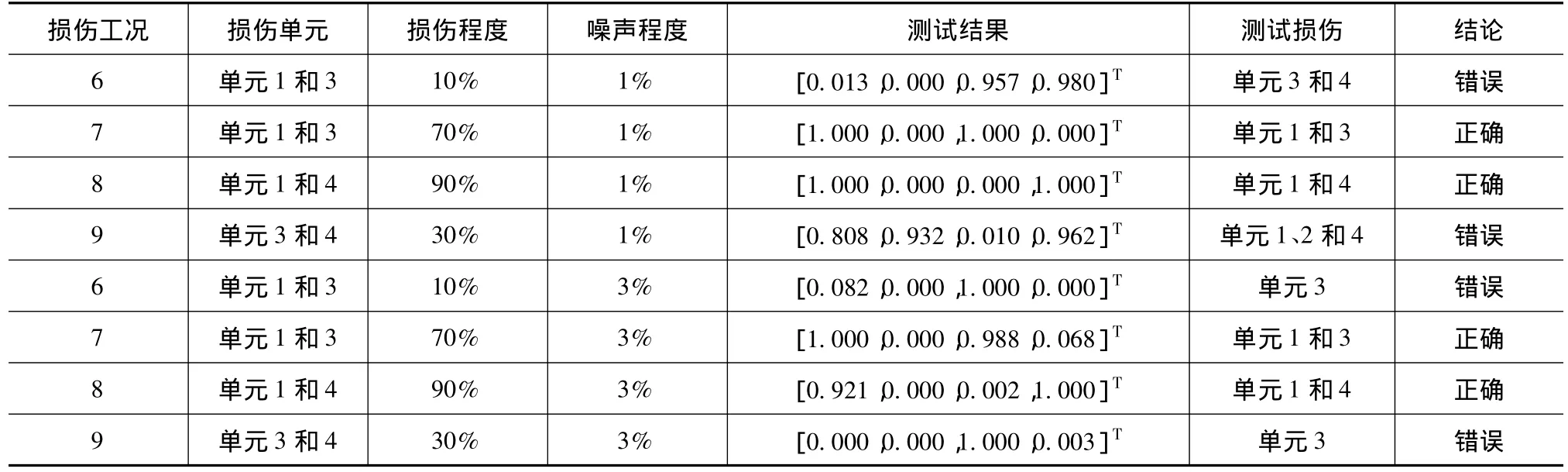
表6 加入白噪声后多损伤的网络训练过程和测试结果

从加入噪声后的测试结果看，该方法对结构发生较大程度损伤时的单处损伤和多处损伤均能准确地进行损伤定位，但是对结构发生较小程度损伤时的损伤定位，不论是单损伤还是多损伤，都出现误判现象。造成误判的原因主要是由于较小程度的损伤引起的结构动力响应相应较小，进而造成结构损伤前后节点能量变化量较小，对损伤定位不敏感。

从未加入噪声和加入噪声后的测试结果看，该方法对结构发生的较大程度损伤能准确地识别出单损伤和多损伤的损伤位置，并且具有较强的噪声鲁棒性，结果令人满意，但是该方法对结构发生较小程度损伤时的单损伤和多损伤的损伤定位具有一定的局限性。

3 结论

直接利用白噪声激励下结构两点响应构造虚拟脉冲响应函数，并对虚拟脉冲响应函数的幅值进行小波包分解并计算其节点能量。以结构损伤前后的小波包节点能量变化量作为损伤特征向量，利用BP神经网络的模式分类功能进行结构损伤定位。从数值模拟结果看，能够很好地对海洋平台结构发生较大程度损伤时的单损伤和多损伤进行损伤定位，并且具有较强的噪声鲁棒性，但是对海洋平台结构较小程度的损伤进行损伤定位具有一定的局限性。另外，对海洋平台结构其它构件损伤位置的识别和损伤程度的识别有待进一步研究。

［1］Biswajit Basu.Identification of stiffness degradation in structures using wavelet analysis［J］.Construction and Building Materials，2005，19:713 －721

［2］Law S S，Li X Y，Zhu X Q.Structural damage detection from wavelet packet sensitivity［J］.Engineering Structures，2005，27:1339－1348

［3］Nichols J M，Virgin L N.Todd M D.On the use of attracter dimension as a feature in structural health monitoring［J］.Mechanical Systems and Signal Progressing，2003，17(6):1305 －1320

［4］Rutolo R，Surace C.Using SVD to detect damage in structures with different operational conditions［J］.Journal of Sound and Vibration，1999，226(3):425 －439

［5］李爱群，丁幼亮.工程结构损伤预警理论及其应用［M］.北京:科学出版社，2007:86－89

［6］刁延松.基于神经网络和小波分析的海洋平台结构损伤检测研究［D］.青岛:中国海洋大学，2006

［7］王柏生，倪一清，高赞明.模型参数误差对用神经网络进行结构损伤识别的影响［J］.土木工程学报，2000，33(1):49 －55