CA砂浆弹模对框架板式轨道翘曲应力的影响分析
周 毅,何燕平,杨荣山
(西南交通大学 土木工程学院,成都 610031)
CA砂浆弹模对框架板式轨道翘曲应力的影响分析
周 毅,何燕平,杨荣山
(西南交通大学 土木工程学院,成都 610031)
采用有限元分析法,对框架板在温度梯度作用下的翘曲应力进行仿真计算,分析了砂浆弹性模量的变化对框架板温度效应的影响。结果表明:在温度荷载作用下,框架板式轨道框架角点处和凸台边缘处将产生局部翘曲应力的集中,最大的翘曲应力产生在轨道板角点处,并产生最大的翘曲位移;随着CA砂浆弹模的增加,轨道板应力集中区域的最大翘曲应力逐渐减小,轨道板角点翘曲位移也逐渐减小。
框架板式轨道 翘曲应力 CA砂浆 有限元法
温度对无砟轨道结构的影响十分明显,轨道板的温度主要指两个方面:一是轨道板整体的温度升降,这使轨道板发生整体的伸缩;二是轨道板沿其高度方向的温度递变即温度梯度,这是轨道板发生翘曲、表层开裂和板底分离的主要原因。为研究CA砂浆层对框架板式轨道翘曲应力的影响,利用ANSYS有限元软件,分析了砂浆弹性模量的变化对框架板温度效应的影响,为无砟轨道的结构设计提供依据。
1 翘曲应力计算基本理论
当物体内部存在温度差,即存在温度梯度时,热量会从物体的高温部分传递到低温部分;两个不同温度的物体相互接触时,热量会从高温物体传递到低温物体,热传导遵循傅立叶定律

式中 q″——热流密度;
k——导热系数或热传导率。
式(1)中负号表示热量流向温度降低的方向。当温度T沿混凝土板厚度x不均匀分布时,板内产生翘曲变形。板顶温度高于板底温度时,板顶面纤维的伸长变形大于底面纤维,板中部便出现向上拱起。而在板顶温度低于板底温度时,板顶面纤维的收缩变形大于底面纤维,板四边出现向上翘起。
2 计算模型与计算参数
温度翘曲应力分为“上热下冷”和“上冷下热”两种,两种情况在板厚方向的温度梯度均按0.5℃/cm线性变化进行计算。考虑到主要分析CA砂浆弹模对轨道板翘曲应力的影响,故只选择“上热下冷”的情况作为分析对象。在计算模型中,轨道板、CA砂浆层、混凝土底座以及凸形挡台均采用实体单元进行模拟。模型中将轨道板分层,并“由上至下”按照线性变化的方式赋于不同的温度荷载,且保证施加温度荷载之和为0。模型中认为砂浆与轨道板以及混凝土底座板的接触是一种完全密贴的全支承状态,故在处理轨道板、混凝土底座板和砂浆的接触条件时,采用粘接方式进行模拟,保证接触面间的位移一致。计算模型如图1所示,计算参数如表1所示。
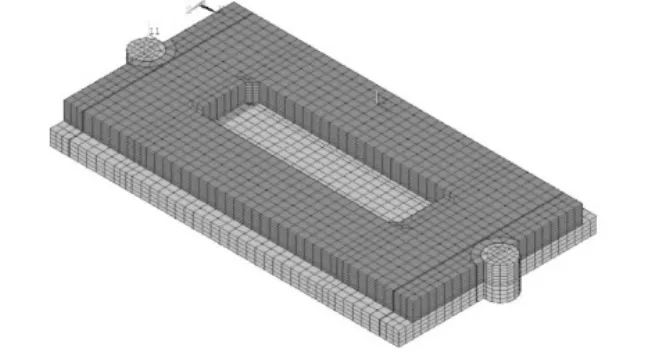
图1 框架板式轨道有限元模型

表1 计算参数
3 计算结果及分析
3.1 翘曲应力和翘曲位移计算
保证其它参数不变,改变CA砂浆层弹性模量,分别计算框架轨道板温度翘曲应力和翘曲位移。计算云图如图2~图4所示。
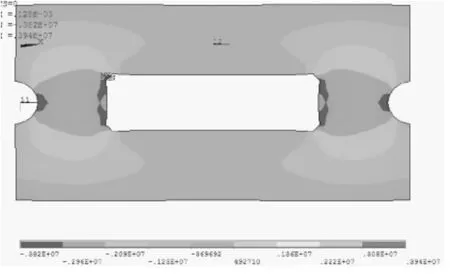
图2 横向翘曲应力分布
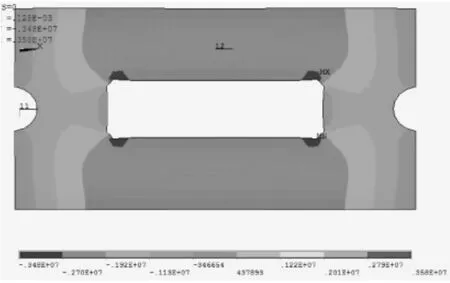
图3 纵向应力分布

图4 翘曲位移分布
由图2~图4可知,在凸台边缘和框架角点处,会发生纵向翘曲应力集中,在凸台边缘与框架边缘之间产生较大的纵向翘曲应力;横向翘曲应力集中发生在框架角点处,在框架边缘与轨道板边缘之间将产生较大的横向应力。在应力集中处,将产生最大的翘曲应力,在轨道板角点处将产生最大的负向翘曲位移,在框架边缘与轨道板边缘之间、凸台边缘与框架边缘之间轨道板将产生一定的上拱变形。不同砂浆弹模下轨道板的最大翘曲应力和翘曲位移如表2所示。
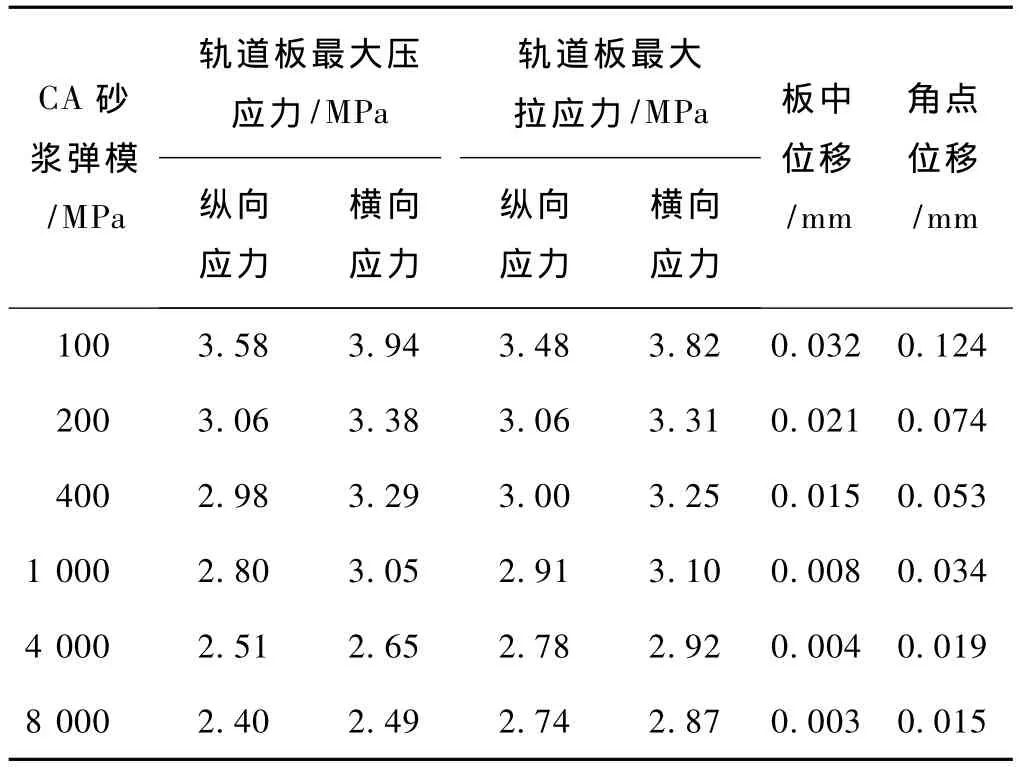
表2 不同CA砂浆弹模下的计算结果汇总
由表2可知,框架轨道板的纵横向最大翘曲应力均随着CA砂浆弹模的增加而减小,横向应力略大于纵向应力,随着CA砂浆弹模的增加,横向应力与纵向应力的差值逐渐缩小。翘曲位移则随着CA砂浆弹模的增加而减小。说明增加CA砂浆弹模可减小轨道板的最大翘曲应力和最大翘曲位移。
3.2 翘曲应力和翘曲位移分布规律研究
根据在不同CA砂浆弹模情况下,计算出的框架板各处的翘曲应力和翘曲位移,分析翘曲应力和翘曲位移随CA砂浆弹模的分布变化的规律。对比分析位置见图5。位置1主要分析轨道板纵向上翘曲应力随砂浆弹模变化的分布规律;位置2主要分析轨道板横向上翘曲应力随砂浆弹模变化的分布规律;位置3主要分析轨道板纵向上翘曲位移随砂浆弹模变化的分布规律;位置4主要分析轨道板横向上翘曲位移随砂浆弹模变化的分布规律。不同CA砂浆弹模下各位置的翘曲应力和翘曲位移分布变化情况如图6~图9所示。
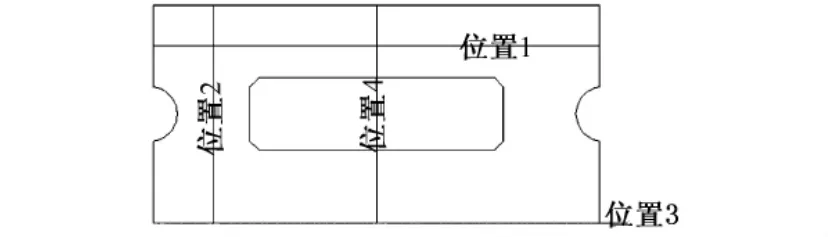
图5 框架板翘曲应力、位移对比分析位置

图6 位置1处轨道板翘曲应力随CA砂浆弹模变化的分布规律
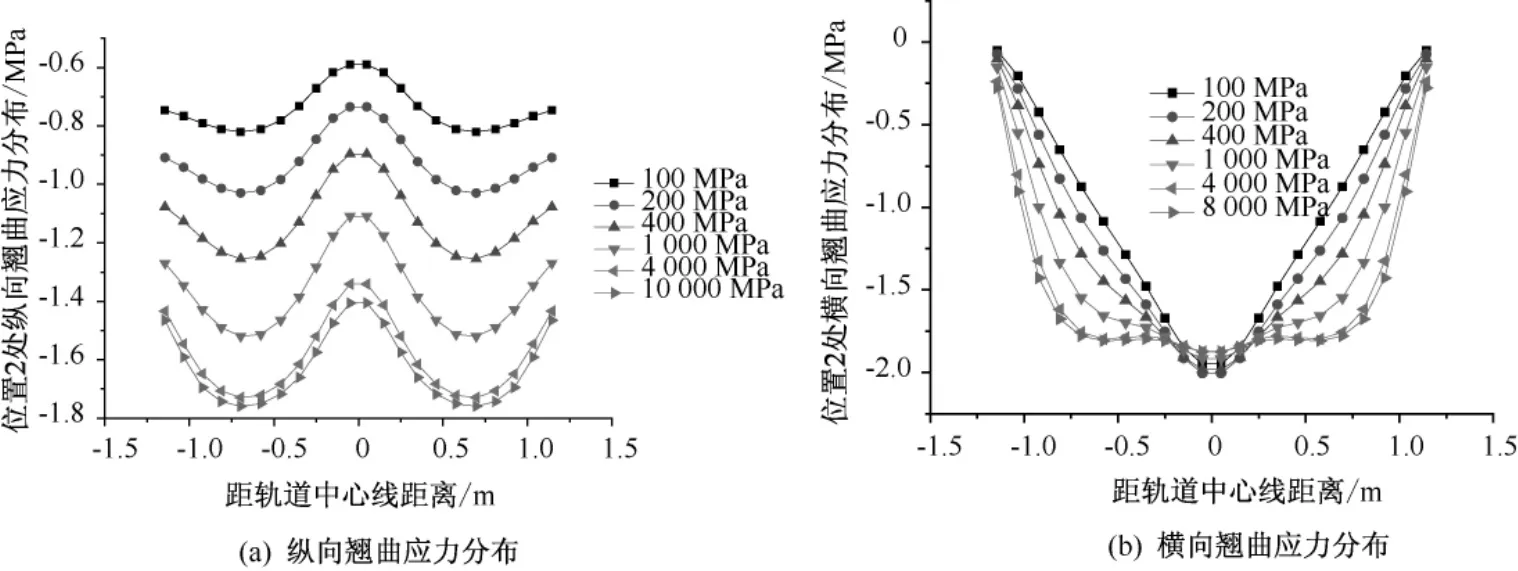
图7 位置2处轨道板翘曲应力随CA砂浆弹模变化的分布规律
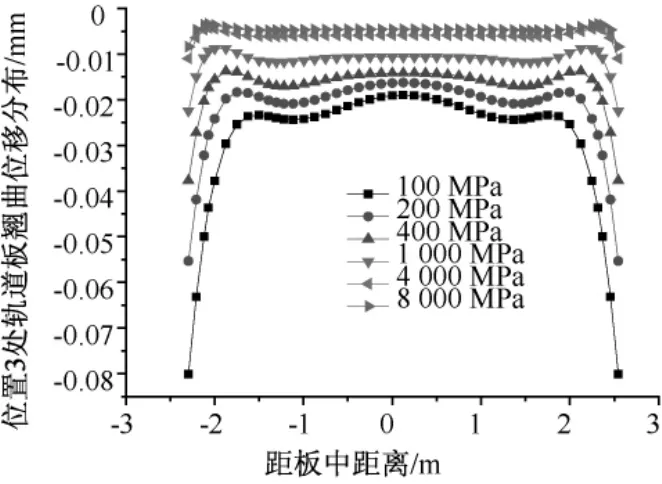
图8 位置3处框架板翘曲位移的分布规律
由图6可知,在轨道板纵向上,轨道板纵横向翘曲应力由轨道板边缘向轨道板中心逐渐增大,在轨道板中心出现应力极值。随着CA砂浆弹模的增加,位置1处的纵横向最大翘曲应力逐渐增大,但翘曲应力由板边向板中的变化幅度逐渐减缓。
由图7可知,在轨道板横向上,轨道板纵横向翘曲应力由轨道板边缘向轨道板中心逐渐增大,在轨道板中心出现应力极值。随着CA砂浆弹模的增加,位置2处的横向最大翘曲应力有所减小,横向翘曲应力由板边到板中的变化幅度逐渐减缓;位置2处的纵向最大翘曲应力逐渐增加,纵向翘曲应力由板边到板中的变化幅度随CA砂浆弹模的增加而有所增加。
由图8和图9可知,在轨道板纵横向上,轨道板的最大翘曲位移均随着CA砂浆弹模的增加而减小,且翘曲位移的分布随着砂浆弹模的增加而趋于均匀。
4 结论
1)在温度荷载作用下,框架板式轨道框架角点处和凸台边缘处将产生局部翘曲应力的集中,产生最大的翘曲应力,在轨道板角点处将产生最大的翘曲位移。随着CA砂浆弹模的增加,轨道板应力集中区域的最大翘曲应力逐渐减小,轨道板角点翘曲位移也逐渐减小,其余部分的翘曲应力逐渐增大,翘曲应力以及翘曲位移由板边向板中的变化幅度逐渐减小。
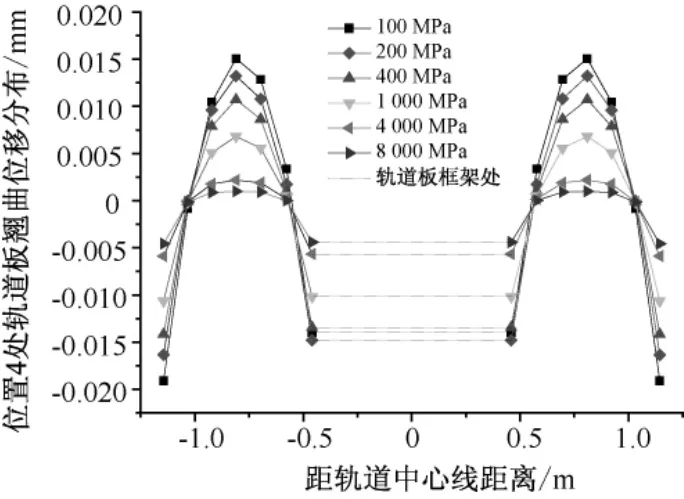
图9 位置4处框架板翘曲位移的分布规律
2)在轨道板纵向上,增加CA砂浆的弹模,会增加轨道板的纵横向翘曲应力,但可以减缓翘曲应力由板边向板中的变化幅度。轨道板在纵向上的翘曲位移则随着CA砂浆弹模的增加而减小,轨道板的翘曲位移在纵向上的分布也趋于均匀。
3)在轨道板横向上,增加CA砂浆的弹模,会增加轨道板的纵向翘曲应力,增加纵向翘曲应力由板边到板中的变化幅度;横向翘曲应力与其变化幅度均随着CA砂浆弹模的增加而有所减小。轨道板在横向上的翘曲位移则随着CA砂浆弹模的增加而减小,轨道板的翘曲位移由板边到板中的变化幅度也逐渐减小。
[1]赵国堂.高速铁路无碴轨道结构[M].北京:中国铁道出版社,2006.
[2]石现峰.温度对板式无砟轨道结构的影响研究[J].铁道工程学报,2008(5):30-32.
[3]王森荣.无砟轨道轨道板温度测量与温度应力分析[J].铁道工程学报,2009(2):52-55.
[4]王秋会.几种特殊无砟轨道板的受力探讨及仿真分析[J].铁道标准设计,2009(增刊):7-9.
[5]高俊英.土质路基上CRTS-I型板温度力分析[D].成都:西南交通大学,2008.
[6]王森荣.板式无砟轨道温度力研究[D].成都:西南交通大学,2007.
[7]赵坪锐,刘学毅.连续道床板温度应力计算方法及参数分析[J].铁道建筑,2008(11):81-85.
U213.2+42
A
1003-1995(2011)03-0103-03
2010-10-02;
2010-12-26
周毅(1986— ),男,四川简阳人,硕士研究生。
(责任审编 王 红)

