简议高中数学分析和解决问题能力的培养

●李小飞 (南京师范大学附属中学 江苏南京 210003)

简议高中数学分析和解决问题能力的培养

●李小飞 (南京师范大学附属中学 江苏南京 210003)

分析和解决问题的能力是指能阅读、理解对问题进行陈述的材料;能综合应用所学数学知识、思想和方法解决问题，包括解决在相关学科、生产、生活中的数学问题，并能用数学语言正确地加以表述．它是逻辑思维能力、运算能力、空间想象能力等基本数学能力的综合体现．由于高考数学的命题原则是在考查基础知识的基础上，注重对数学思想和方法的考查，注重数学能力的考查，强调了综合性．这就对考生分析和解决问题的能力提出了更高的要求，也使试卷的题型更新，更具有开放性．

1 分析和解决问题能力的组成

1．1 审题能力

审题能力主要是指充分理解题意，把握住题目本质的能力;分析、发现隐含条件以及化简、转化已知和所求的能力．要快捷、准确地解决问题，掌握题目的数形特点、能对条件或所求进行转化和发现隐含条件是至关重要的．

从上述解答过程可以看出，解决此题的关键在于挖掘所求和已知条件之间的联系，这需要有一定的审题能力．由此可见，审题能力应是分析和解决问题能力的一个基本组成部分．

1．2 合理应用知识、思想、方法解决问题的能力

高中数学知识包括函数、不等式、数列、三角函数、复数、立体几何、解析几何等内容;数学思想包括数形结合、函数与方程思想、分类与讨论和等价转化等;数学方法包括待定系数法、换元法、数学归纳法、反证法、配方法等基本方法．只有理解和掌握数学的基本知识、思想、方法，才能解决高中数学中的一些基本问题，而合理选择和应用知识、思想、方法可以使问题解决得更迅速、顺畅．

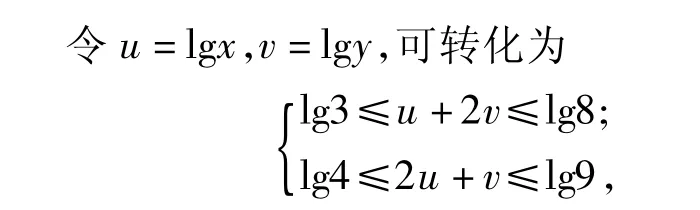
求3u－4v的最大值．不难发现这是个线性规划问题，仍然可以用数形结合的思想来解决．

1．3 数学建模的能力

例3某兴趣小组测量电视塔AE的高度H(单位:m)，如图 1，垂直放置的标杆BC的高度h=4 m，仰角∠ABE=α，∠ADE=β．

(1)该小组已经测得一组α，β 的值，tanα =1．24，tanβ =1．20，请据此算出H的值．

(2)该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d(单位:m)，使α与β之差较大，可以提高测量精确度．若电视塔的实际高度为125 m，试问d为多少时，α－β最大?

分析本题主要考查解三角形的知识、两角差的正切及不等式的应用．

图1

本题第(2)题的文字表述比较长，要求学生能够将文字语言转化为数学语言，能够把求α－β的值最大转化为求该角的三角函数值最大．文字语言转化为数学语言从而再进一步转化为数学问题，是学生难以掌握的地方．这需要提高文字信息的获取能力和数学建模能力．平时在教学过程中，教师要试着让学生独立阅读题目，并尝试自己寻找信息，从而将问题转化为数学问题．

当然，本题也可以利用几何知识来解决，过点E作AD的平行线，当以BC为弦的圆与直线AD相切时，α－β的值最大．这样，就可以利用切割线定理很快得到答案．

2 培养和提高分析、解决问题能力的策略

2．1 重视通性通法教学，引导学生概括、领悟常见的数学思想与方法

数学思想较之数学基础知识，有更高的层次和地位．它蕴涵在数学知识发生、发展和应用的过程中，是一种数学意识，属于思维的范畴．数学方法是数学思想的具体体现，具有模式化与可操作性的特征，可以作为解题的具体手段．

在数学课堂教学中应重视通性通法，淡化特殊技巧，使学生认识一种“思想”或“方法”的个性，即认识一种数学思想或方法对于解决什么样的问题有效．从而培养和提高学生合理、正确地应用数学思想与方法分析、解决问题的能力．

2．2 加强应用题教学，提高学生的模式识别能力

高考是注重能力的考试，特别是学生运用数学知识和方法分析问题、解决问题的能力，而高考中的应用题就着重考查这方面的能力．

数学是充满模式的，就解应用题而言，对其数学模式的识别是解决它的前提．由于高考考查的不是原始的实际问题，命题者对生产、生活中的原始问题的设计加工使每个应用题都有其数学模型．在高中数学教学中，不但要重视应用题的教学，同时要对应用题进行专题训练，引导学生总结、归纳各种应用题的数学模型，这样学生才能有的放矢，合理运用数学思想和方法分析、解决实际问题．

2．3 适当进行开放题和新型题的训练，拓宽学生的知识面

要分析和解决问题，必须先理解题意，这样才能进一步运用数学思想和方法解决问题．近年来，随着新技术革命的飞速发展，要求数学教育培养出更高数学素质、具有更强创造能力的人才，这一点体现在高考上就是一些新背景题、开放题的出现，更加注重了能力的考查．由于开放题的特征是题目的条件不充分，或没有确定的结论，而新背景题的背景新颖，给学生在题意的理解和解题方法的选择上制造了不少的麻烦，导致失分率较高．因此，在高中数学教学中适当进行开放题和新型题的训练，拓宽学生的知识面是提高学生分析和解决问题能力必要的补充．

2．4 重视解题的回顾

在数学解题过程中，解决问题以后，再回过头来对自己的解题活动加以回顾与探讨、分析与研究，是非常必要的一个环节．这是数学解题过程的最后阶段，也是对提高学生分析和解决问题能力最有意义的阶段．

解题教学的目的并不单纯为了求得问题的结果，真正的目的是为了提高学生分析和解决问题的能力，培养学生的创造精神，而这一教学目的恰恰需通过回顾解题的教学来实现．

因此，在数学教学中要重视解题的回顾，与学生一起对解题的结果和解法进行细致的分析，对解题的主要思想、关键因素和同一类型问题的解法进行概括，帮助学生从解题中总结出数学的基本思想和方法并加以掌握，将其用到新的问题中去，成为以后分析和解决问题的有力武器．