机构结构新旧自由度计算公式对比之应用研究

蔡汉忠 欧阳富 廖明军

北华大学，吉林，132013

机构结构新旧自由度计算公式对比之应用研究

蔡汉忠 欧阳富 廖明军

北华大学，吉林，132013

通过对机构结构新旧自由度计算公式的对比研究及应用发现：新公式和库兹巴赫·格鲁巴（Kutzbach Qruber）公式是正确的。这2个公式能计算所有平面、空间机构结构的自由度，用这2个公式计算的非圆齿轮液压马达、奥迪A6轿车01V自动变速器行星排机构、六角形6－SPS和三角形6－RUS空间并联机构及平面、空间结构力学习题集的自由度，都取得了正确的计算结果。

封闭环约束数（阶数）；多余自由度；封闭环；结构

0 引言

随着自由度计算公式的研究拓展，人们追求公式本身在实际机构自由度计算时的正确性、科学性、真实性和广泛性更加迫切。

经多年研究与计算结果比较，发现新公式［1］和Kutzbach Qruber公式（简称K氏公式）是正确的。这两个公式可以计算任何平面、空间机构、机器人机构和自动变速器及各种力学中的自由度，由此可以说明新公式和K氏公式揭示了机构结构运动的本质规律和内在联系。在3万个实例计算中，这两个公式都可以得到相同的结果，同时也发现在结构力学中K氏公式不如新公式实用性广。

本文基于文献［1］的理论研究，对机构结构新自由度计算公式进行实例分析。

1 关于5类自由度计算公式的回顾［1］

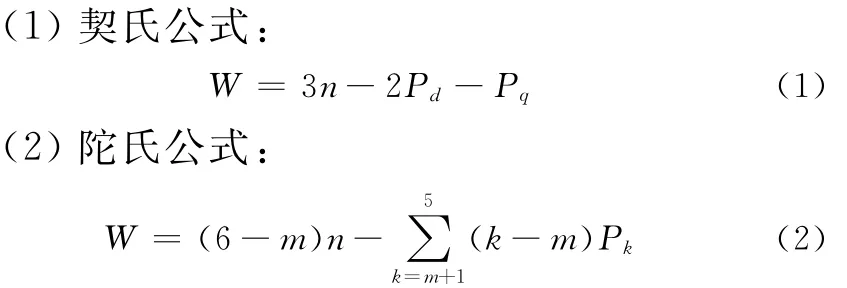
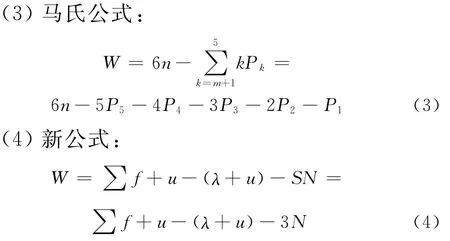
当空间机构没有S－S球面副自转自由度u时，式（4）可表示为

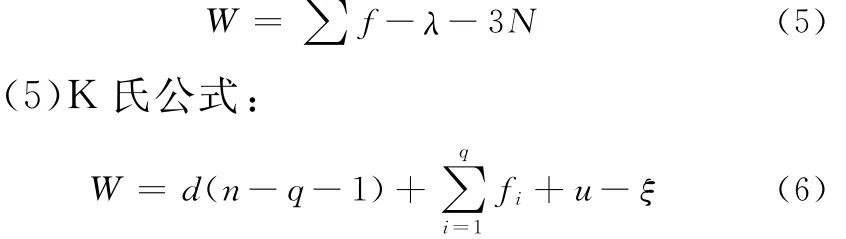
在文献［1］中，已将公式中的各参数作了详细的说明，这里不再介绍，但必须强调式（5）和式（6）在本质上是相同的。

2 自由度计算公式在实际中的应用举例

例1 用契氏公式、陀氏公式、新公式、K氏公式计算图1所示非圆齿轮1、3和圆柱行星齿轮2在环形空间，由非圆齿轮1驱动，各个密闭腔的容积作周期性变化的液压马达的自由度W［2］。

（1）用契氏公式计算：

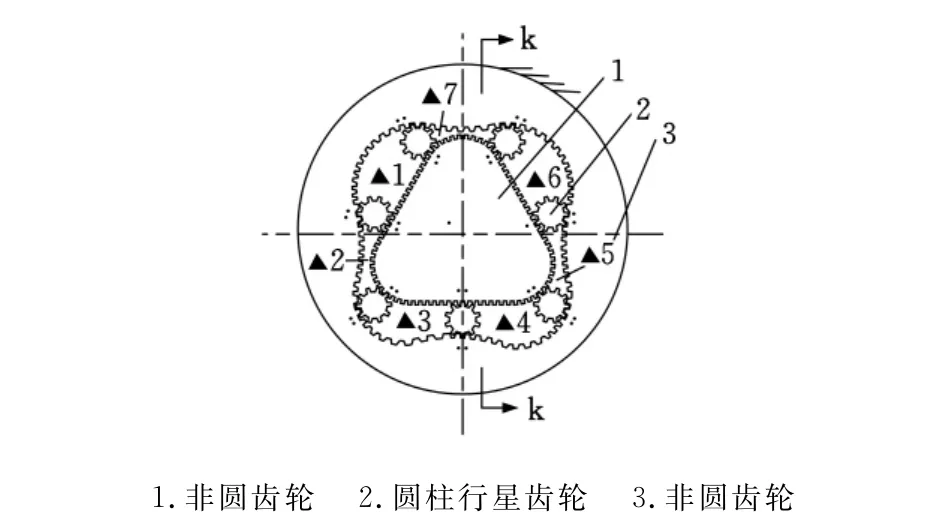
图1 非圆齿轮驱动的液压马达

例2 用契氏公式、陀氏公式、新公式、K氏公式计算图2所示奥迪A6轿车01V自动变速器的自由度W 及各挡自由度。

（1）用契氏公式计算：

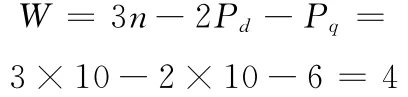
W＝4，说明奥迪A6轿车01V自动变速器有4个前进挡（不含超速挡和倒挡）。从图2中查得n＝11。

（2）用陀氏公式计算：

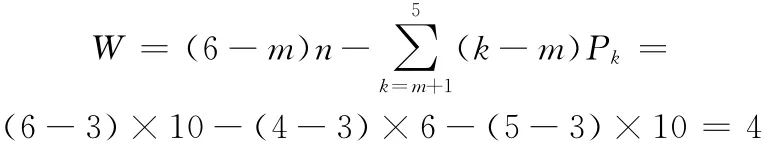
（3）用新公式计算。由于长齿轮中心轴上有两个自由度，其中一个为共轴多余自由度λ＝1，长齿轮中心轴上真正起作用的自由度只有一个。

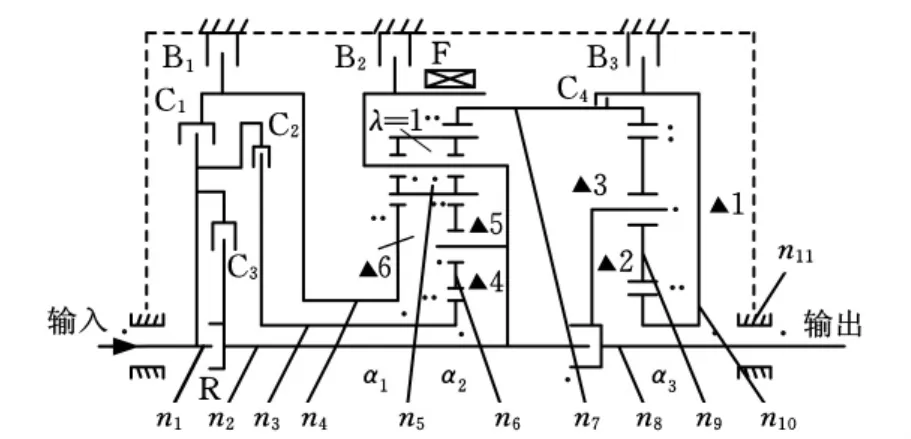
图2 奥迪A6轿车01V自动变速器行星排机构［3］

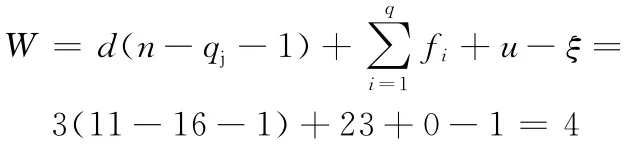
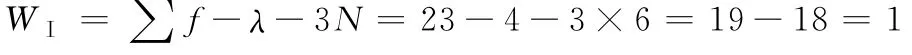
按Ⅰ挡计算方法类推，可求出 Ⅱ、Ⅲ、Ⅳ、Ⅴ挡和倒挡R的自由度都等于1。当计算得出W＝4后，不计倒挡和超速挡，根据行星排的数目即可写出图2的3个转速方程式：

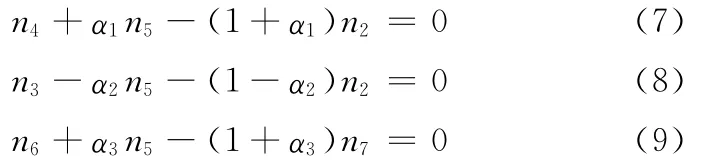
根据这3个方程式，前进挡不工作时即有α1＝0，再根据使用离合器、制动器和单向离合器F的情况，可以求出各挡位的传动比i。我国研制的自动变速器的自由度W ＝8。

例3 用新公式、K氏公式、契氏公式、陀氏公式计算图3所示带有六角形6－SPS并联空间机构的自由度［4］。

（1）用新公式计算。由空间平台机构理论知，用式（5）计算的图2所示奥迪汽车行星排机构的自由度为W＝∑f－λ－3 N＝23－1－3×6＝4，由于有λ＝1，所以式（6）中q将变成qj＝qzqy＝17－1＝16，这里的qj表示多余约束数的计算数，qz表示多余约束数的总数，qy表示多余约束数的余数，且qy都是由于λ＝1而减少的数。

（4）用K氏公式计算：它至少需要3个分支传动机构支撑平台，因为三角形具有稳定性。图3所示六角形6－SPS机构由2个三角形平台构成，按对称取半原则，故取3－SPS为一组进行计算。每支SPS机构的自由度总数∑f＝7，多余自由度总数为λz＝4×3＝12，3支的封闭环数为N＝2，将这些新数据代入式（5），得一组3－SPS机构的自由度为W1＝∑f－λ－3 N＝3×7－4×3－3×2＝21－18＝3，两组3－SPS构成6－SPS空间机构，其自由度为W＝2×W1＝2×3＝6，W ＝6，采用6个液压缸或气缸等直线驱动方案即可。

（2）用K氏公式计算。先计算一组3－SPS空间机构的自由度，得

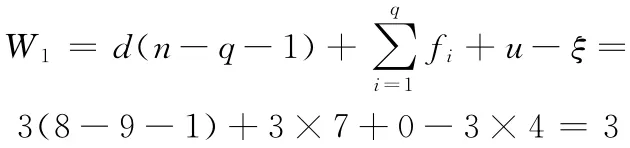
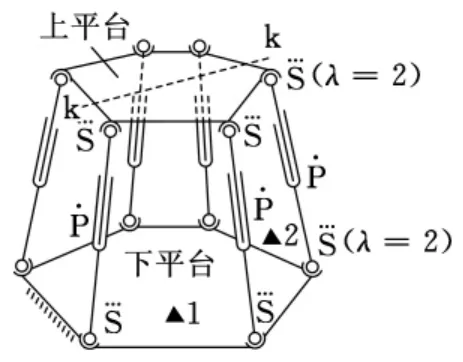
图3 六角形6－SPS空间机构

由两组3－SPS构成的6－SPS空间机构的自由度为

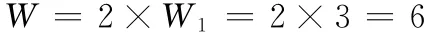
（3）用契氏公式计算3－SPS机构的自由度，有

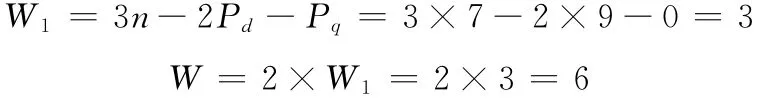
（4）用陀氏公式计算，有

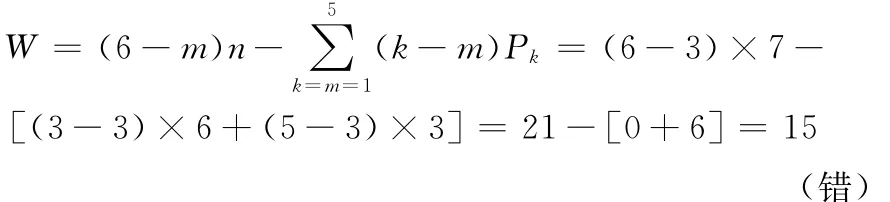
同理，可分析计算三角形6－RSS卧式、三角形6－SPS和三角形3－SPS、三角形6－RSS立式、6－PUS、6－RUS、6－SRRR 等空间机构的自由度。

例4 用新公式、K氏公式、契氏公式、陀氏公式计算图4所示带有等边三角形6－RUS并联空间机构的自由度［4］。图4中三角形GHI是中心上平台，它可以作为机器人操作机构的输出杆件，在三维空间具有6个自由度。此上平台有6个分支并联地与下平台相联，每个分支用2个杆件串联。采用3种不同的运动副R、U、S形式进行，在上平台等边三角形顶点是球面副复铰，A、B、C、D、E、F为6个万向节U（即虎克铰），每个万向节的自由度为2，λ＝1；每个球面副的自由度为3，λ＝2；A、B、C、D、E、F 只能在XOY 基面内运动，6点到中心O（R）的杆长相同。另外，连接上平台的6个倾斜杆长为L2。再作运动分析：每个分支（每条腿）有6个自由度，在下平台中心O有6个杆件是输入主动杆件，皆由主动杆与X轴的夹角来确定。

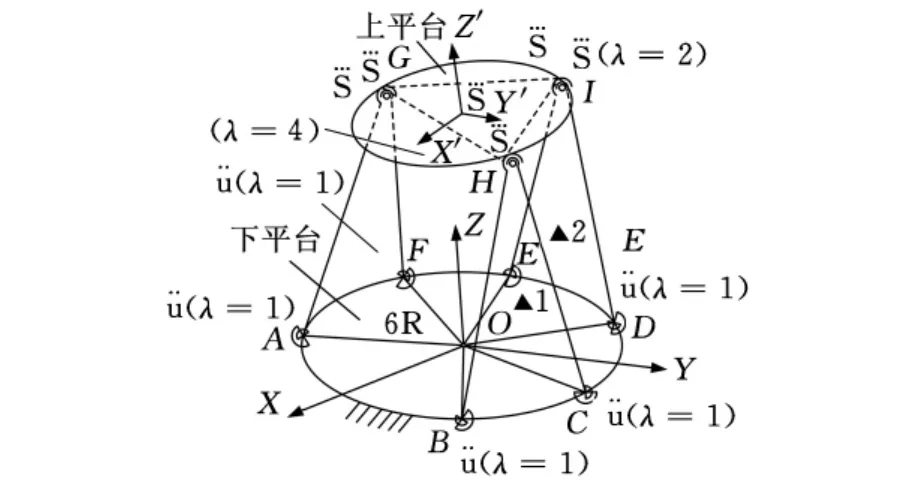
图4 三角形6－RUS空间机构

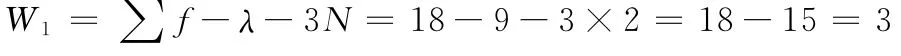
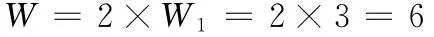
W＝6，说明该空间机构分别由6个主动副R的转动所驱动。

（2）用K氏公式计算：

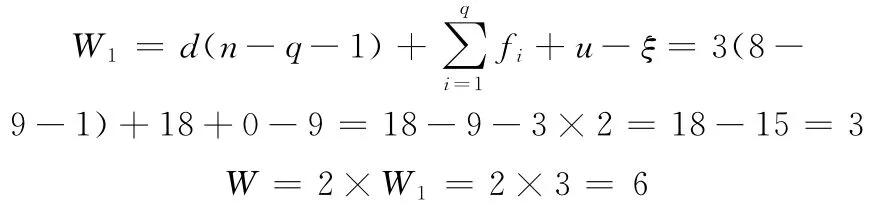
（3）用契氏公式计算：

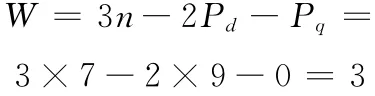
（4）用陀氏公式计算：

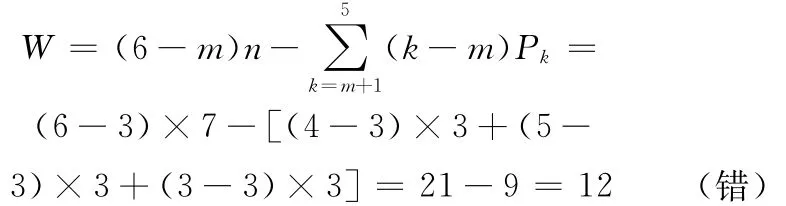
3 新公式和K氏公式在结构力学中的应用

在式（5）中去掉多余自由度λ和自转多余自由度u两项，就得到结构力学、工程力学、建筑力学和弹性力学等计算自由度的公式［5-6］：

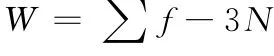
众所周知，在现代结构力学中使用的自由度W 计算公式有三种［7］：一种是取刚片为研究对象，结点和支杆为约束；一种是取结点为研究对象，约束为链杆；第三种是混合法，既取刚片又取结点为研究对象，约束为结点和链杆。不管哪种算法，对象的选择一般不困难，而约束数的计算有的不容易弄清。现将图5所示三种算法的自由度计算公式表示如下：

式中，m为刚片数，m＝8；b为简单链杆数，b＝4；g为刚结点数，g＝7；h为绞结点数，h＝1；d为内部多余约束数，d＝3。j为取作对象的绞结点数（包括支座结点数，固定端算1个结点）。

式（10）、式（12）、式（13）三式符号含义不完全相同，用式（13）计算时，其中，m ＝1（AGPEHB 部分），d＝3，h＝0，g＝0，b＝5，j＝1（铰链C，因铰链A、B、E与取作对象的刚片m7、m8相连，不计算j），下面用几个公式分别计算图5所示结构体系的自由度。

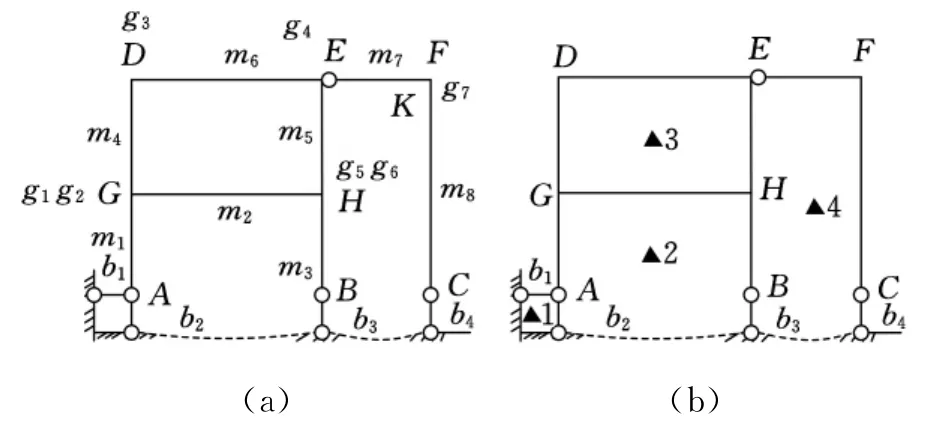
图5 结构力学中的刚架支座结构

（1）用式（10）计算。已知m ＝8，g＝7，h＝1，b＝4，则

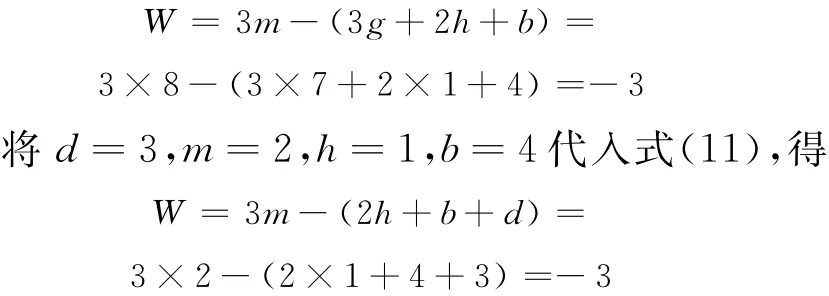
第二种算法中大刚片内有一个封闭环的约束数d＝3。

（2）用结点法计算。式（12）中的铰结点数为4（含A、B、C、E4个铰结点，b是含支座链杆的简单链杆数，b＝8，连接A、B、C3个结点，有2n－3个简单链杆（n＝3），即2×3－3＝3，故b＝3＋1＋4＝8（其中包括CE 杆和4个支座杆），d为GHED封闭环内的约束数，d＝3，代入式（12），得

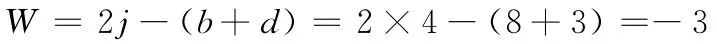
（3）用混合算法计算。将AGDEHB视为一个刚片，有m＝1，GDEF为一个封闭环，每个封闭环有3个约束数，故d＝3，因铰A、B、E与取作对象的刚片相连，j＝1（铰C），b＝5（支杆数），g＝0，h＝0，代入式（13），得

由此可见，应用式（5）只要掌握结构力学中复铰的自由度数比连接复铰的杆件数少一个即可，这种计算结构力学自由度的方法比结构力学现有公式来得简单、方便、快捷。

4 结论

（1）新公式与K氏公式是平面、空间机构自由度计算公式中最优的公式，其他公式都无法与之相比［1］。

（2）在结构力学自由度计算中，新公式可适用于全部结构力学自由度的计算，而K氏公式只适用于其中一部分。

（3）在自动变速器自由度计算中，新公式只要求正确确定一个多余自由度λ和封闭环数N两个因子，而K氏公式除要求确定消极自由度ξ和局部自由度u外，对于自动变速器，还要求考虑含机架在内的杆件数n和含高低副在内的运动副数q4个因子，才能正确地画出符合实际的机构原理图［1］。

（4）在并联多封闭环空间机构的任何情况下，新公式可以一次完成计算，而K氏公式有时需要两次才能完成计算。

（5）新公式和K氏公式都有相同的二杆、三杆和杆件数大于或等于四杆的自由度计算公式。

（6）新公式的约束数m和K氏公式的阶数d相等，即有m＝d＝3，它们都等于传统的公共约束数。

（7）新公式中的－N等于K氏公式中括号内的数值（－N＝（n－q－1），因此新公式与K氏公式完全相同。

（8）在新公式中，若λ＝0，则可得到结构力学、工程力学、材料力学、弹性力学、桥梁等专门学科自由度的计算公式。

［1］ 欧阳富，蔡汉忠，廖明军.机械结构新旧自由度计算公式对比之理论研究［J］.中国机械工程，2010，21（24）：2942－2948.

［2］ 李华敏，李瑰贤，王知行，等.齿轮机构设计与应用［M］.北京：机械工业出版社，2007.

［3］ 过学凡.汽车自动变速器——结构·原理［M］.北京：机械工业出版社，2002.

［4］ 黄真.空间机构学［M］.北京：机械工业出版社，1991.

［5］ 欧阳富，张士成，刘彦华，等.关于重建平面、球面机构自由度计算新公式的研究［J］.机械工程学报，2002，38（11）：47－52.

［6］ 欧阳富，刘彦华，孙东明.关于重新建立空间机构自由度计算公式的探索［J］.机械工程学报，2003，39（1）：60－64.

［7］ 雷钟和，江爱川，郝静明，等.结构力学解疑［M］.北京：清华大学出版社，2001.

Comparable Study and Application on New and Old Formulas of Calculating DOFs of Mechanisms and Structures

Cai Hanzhong Ouyang Fu Liao Mingjun
Beihua University，Jilin，Jilin，132013

According to comparable study and application on new and old formulas for calculating DOFs of mechanisms and structures，the new formula was proved to be correct，as well as Kutzbach Qrubler Formula.These two formulas work for all the DOF calculation in plain and space mechanisms，and reveal the basic law of kinetic mechanisms and structures.With the new formula，the structures and number of DOFs was checked correctly in non－circular gear hydraulic motor，in AUDI 01V auto transmission planet row，hexagon 6－SPS and triangle 6－RUS spatial parallel mechanism and problem sets for plane and space structural mechanics.

loop constrain number（order number）；surplus DOF；closed loop；structure

TH112

1004—132X（2011）01—0035—04

2010—02—23

2010—12—30

（编辑 何成根）

蔡汉忠，男，1975年生。北华大学交通建筑工程学院讲师。主要研究方向为生物机构自由度。发表论文3篇。欧阳富，男，1942年生。北华大学交通建筑工程学院教授。廖明军，男，1974年生。北华大学交通建筑工程学院副教授、博士。