定量基因扩增仪热循环系统建模与分析

姚英豪 陈章位 黄 靖 刘娟容

浙江大学流体传动及控制国家重点实验室，杭州，310027

定量基因扩增仪热循环系统建模与分析

姚英豪 陈章位 黄 靖 刘娟容

浙江大学流体传动及控制国家重点实验室，杭州，310027

根据热、电传递规律的相似性，建立了基于热电制冷器的定量基因扩增仪（PCR仪）热循环系统的等效电路模型，用电路分析方法研究热传导问题。通过电路仿真软件Multisim10对该系统进行仿真，分析系统稳态、动态特性，以及散热器热阻对系统性能的影响。在热循环系统的设计、优化和控制中采用该等效电路模型进行分析是一种简单有效的方法。

定量基因扩增仪（PCR仪）；热电制冷器；热循环系统；等效电路模型

0 引言

定量基因扩增仪（PCR仪）是目前基因分析领域常用的仪器设备之一［1］，能在短时间内在体外大量扩增特定的DNA片段，并利用荧光信号实时监测PCR进程，实现对模板DNA的定量。定量PCR仪的核心组成部分——热循环系统，能够使DNA样本达到PCR技术要求的变性、退火、延伸温度，并保持一定时间，且不断循环。因为热电制冷器（thermoelectric cooler，TEC）［2］具有体积小、重量轻、无噪声、可靠性高、制冷／加热迅速、使用方便等特点，目前大多数PCR仪热循环系统采用热电制冷器作为加热制冷元件。

国内外对热电制冷器的研究主要侧重于其稳态下的制冷特性、工作参数的优化等，对基于热电制冷器的系统在稳态和非稳态下的性能研究还不多［3］。而PCR反应需在不同温度下循环，且各温度段的维持时间较短（20～30s），为使DNA样品快速、准确、稳定地达到目标温度，对制冷和加热工作模式下的热循环系统的动态性能进行研究显得尤为重要。传统的解析法和数值计算方法过程复杂，不便于分析［4］。近年来，根据热、电传递规律的相似性提出的热电模拟方法，计算简便而有效［5－7］。本文采用该方法建立了热循环系统的等效电路模型，通过电路仿真软件 Multisim10［8］仿真分析了系统的稳态和动态性能，以及散热器热阻对系统性能的影响。

1 系统等效电路模型

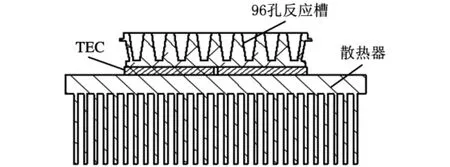
图1 热循环系统物理模型

定量PCR仪热循环系统主要由96孔反应槽、热电制冷器和散热器组成，其物理模型如图1所示。96孔反应槽用于放置装有DNA样本的试管，热电制冷器加热或制冷时使96孔反应槽温度上升或下降，从而使DNA样品温度满足PCR反应条件。系统加热时，热电制冷器将散热器端的热量传递到96孔反应槽；系统制冷时，热电制冷器吸收96孔反应槽端的热量传递到散热器端。为提高热电制冷器的制冷效果，除了选用合适的散热器外还需要通过风扇提高散热性能。96孔反应槽处于密闭空间内，为避免试管中的DNA样本因高温蒸发掉，96孔反应槽上方为恒温104℃的热盖。热电制冷器与96孔反应槽和散热器之间用导热硅胶连接。

根据热、电传递规律的相似性，可应用类似电学中欧姆定律和电路网络理论等方法来研究传热现象。热学相关的物理量可以等效为相应的电学量，具体如表1所示。

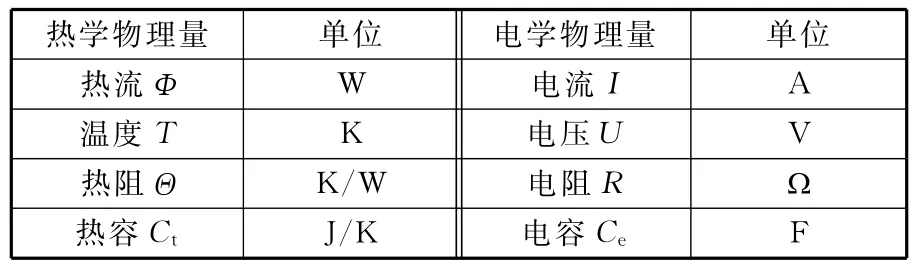
表1 热、电参数类比

1.1 热电制冷器的等效电路模型

热电制冷器是由多对电偶联结而成的热电堆，如图2所示，利用Peltier效应［9］，可实现TEC上端所接系统的加热与制冷。当电流由N通过P时，在半导体与金属导体一端的接合处吸热（冷端），而在另一端放热（热端），产生温差。当电流方向反向时，吸热与放热端互换。由于本系统中的热电制冷器同一面既可能是冷端面又可能是热端面，故为分析方便，本文定义热电制冷器与96孔反应槽接触的一端为控制端，与散热器接触的一端为非控制端。

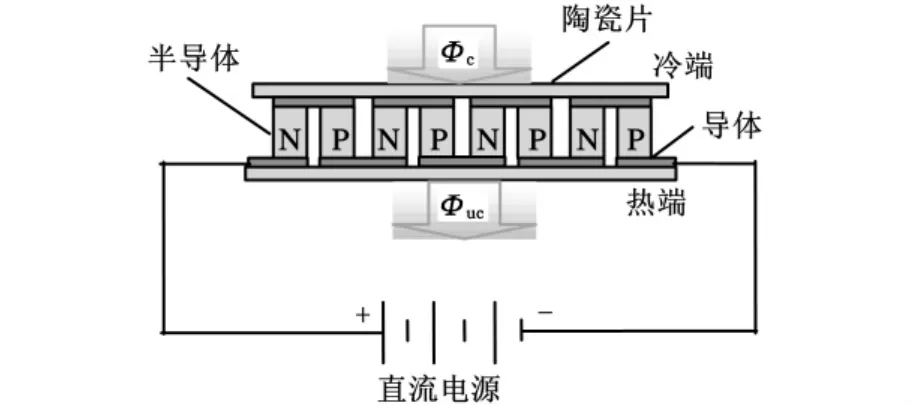
图2 热电制冷器工作原理

根据热电制冷器的特性及能量守恒定律和传热学理论，热电制冷器的数学描述如下［10］：

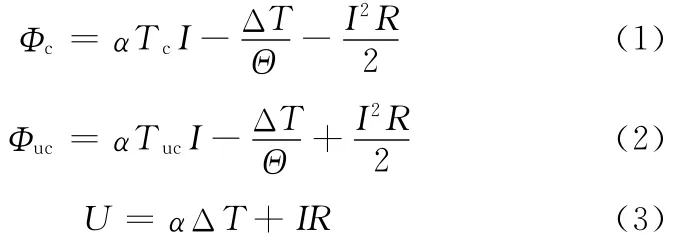
式中，Φc为控制端吸收的热流量；Φuc为非控制端释放的热流量；Tc为控制端温度；Tuc为非控制端温度；α为热电制冷器的塞贝克系数；R为热电制冷器的等效电阻；Θ为热电制冷器的热阻；I为通过热电制冷器的电流；U为热电制冷器两端的电压；ΔT为热电制冷器两端的温差。

由上述数学模型可得到热电制冷器的等效电路模型［5］，如图3所示。相关的系数可从热电制冷器制造商提供的参数中计算提取［6］。本文采用的热电制冷器是Marlow公司生产的XLT2389产品，其相应的参数如表2所示［11］。Ct为热电制冷器和其两端陶瓷片的总热容，其值为5.68J／K［11］。

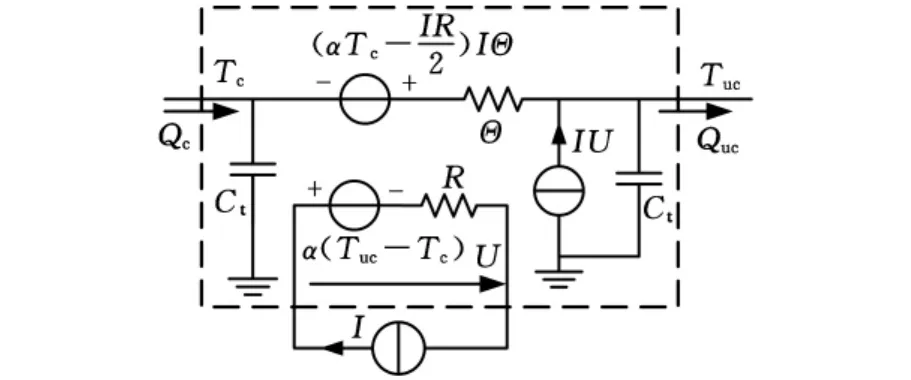
图3 热电制冷器等效电路模型

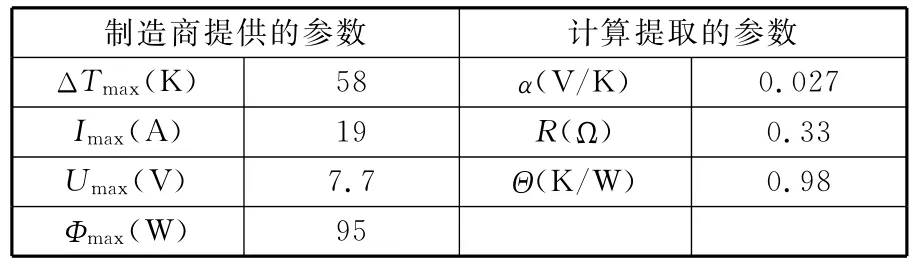
表2 热电制冷器相关参数

1.2 热循环系统等效电路模型

热循环系统的物理结构如图1所示，本文中采用4片热电制冷器串联工作。假设各物体间接触良好，即忽略物体间的接触热阻及其他附加热阻，则系统等效电路模型，如图4所示。其中，αm、Rm、Θm分别为4片热电制冷器串联后的总塞贝克系数、电阻和热阻；Θiso为96孔反应槽与热盖之间密闭空气的热阻；Θplate为96孔反应槽的热阻；Θcont为96孔反应槽与热电制冷器控制端间导热硅胶的热阻；Θsink为散热器的热阻；Cplate为96孔反应槽的热容；Csink为散热器的热容；Tamb为环境温度；Tcover为热盖温度。

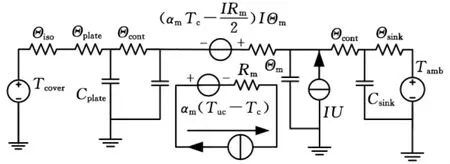
图4 热循环系统等效电路模型

1.2.1 反应槽热阻与热容计算

为简化模型，方便计算，将96孔反应槽等效为长L、宽W、高H的平板。其传热过程可近似为一维导热问题。通过96孔反应槽的热流量Φ，由傅里叶定律可得

式中，M为96孔反应槽质量；c为96孔反应槽比热；ρ为96孔反应槽密度；V为96孔反应槽体积。

1.2.2 散热器热阻与热容计算

本系统采用普通矩形肋片散热器。由传热学公式可得通过肋壁的传热量如下：基座的导热

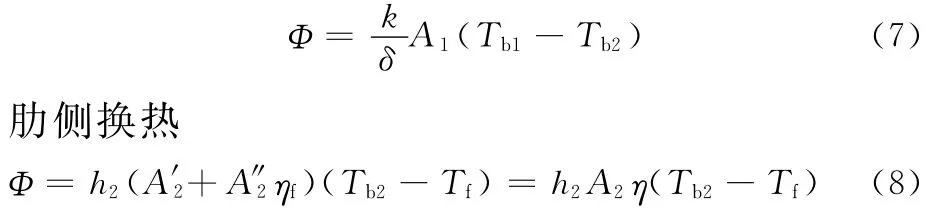
式中，δ为散热器基座厚度；A1为基座导热面积；Tb1为基座光面温度；Tb2为基座肋侧面温度；h2为表面换热系数；A′2为肋间面积；A"2为肋片面积；ηf为肋片效率；Tf为空气温度；η为散热器总效率。

系统仿真参数如表3所示。

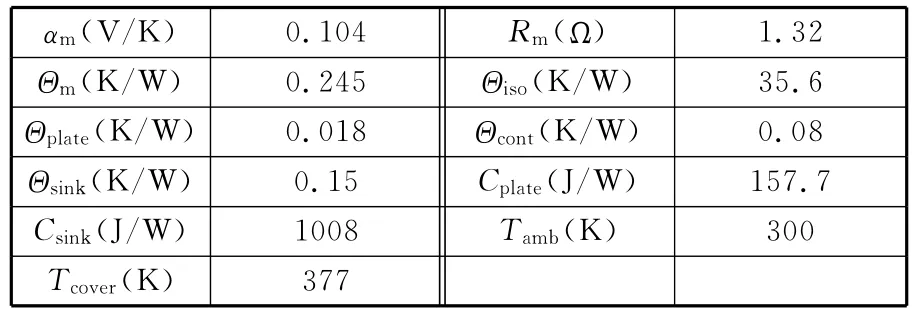
表3 系统仿真参数

2 系统仿真分析

2.1 系统稳态性能分析

用Multisim10中的DC Sweep功能可分析热循环系统在不同电流作用下处于稳态时96孔反应槽的温度情况，如图5、图6所示。实验测得的数据与仿真结果基本吻合。

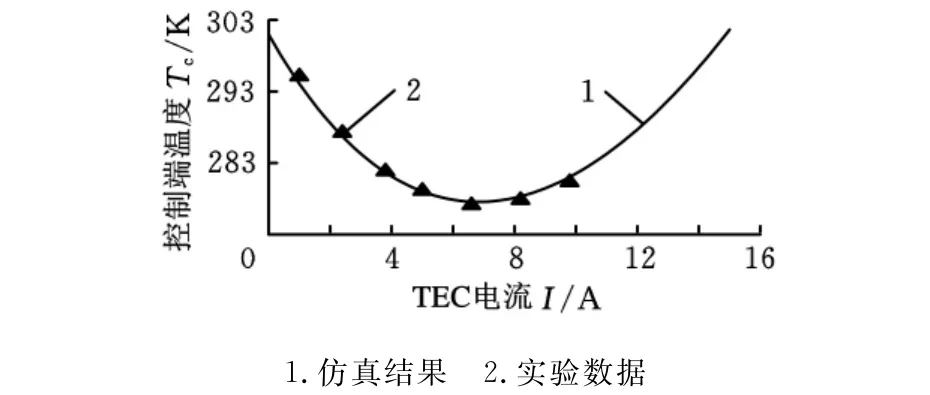
图5 制冷模式下系统稳态特性

由图5可知，系统在制冷模式下控制端温度并不是随着驱动电流的增大而一直降低，当驱动电流增大到一定值后控制端温度反而升高。这主要是由于热电制冷器内阻R上的热功率I2R随电流增大而增大，使控制端吸热流量减小甚至出现负值所引起的。为此在闭环系统的设计中要特别注意制冷时电流的工作范围。如图6所示，系统加热模式下控制端温度随电流一直升高，但具有较明显的非线性特征，在闭环控制系统的设计中应引起足够的重视。

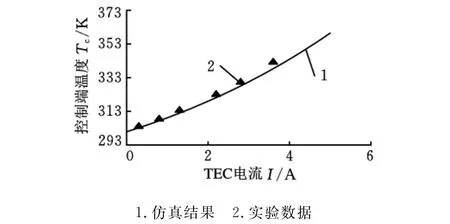
图6 加热模式下系统稳态特性

2.2 系统动态性能分析

Multisim10中的瞬态分析功能可以用来研究热循环系统的非稳态性能。系统在加热和制冷模式下的阶跃响应如图7所示，实验测得的数据与仿真结果基本吻合。从仿真结果看，系统动态响应时间较长，且在同样大小电流作用下加热效率要高于制冷效率。

图7 系统加热和制冷时动态特性

不同电流作用下系统的阶跃响应如图8、图9所示。图8所示为系统在加热模式下不同电流对阶跃响应的影响，图9所示为制冷模式下的情形。从图8可以看出，在加热模式下，系统响应随电流增大而变快，增大电流可以使系统更快地获得更大的稳态温度，但在制冷时并不意味着电流越大越好。从图9可以看出：在大电流（如18A电流）作用下，系统能较快开始降温，但降温能力有限，当降到9℃（282K）左右时开始出现反弹，之后温度持续上升；在小电流如8A电流作用下，控制端温度能持续下降而不会出现反弹，但开始阶段响应较慢。因此，在闭合控制系统设计时若想获得较快的降温速度，可以在降温初期用较大的电流并逐渐减小电流避免出现温度反弹。为此，需要通过实际调试，选择合适的电流和作用时间以达到较好的降温性能。

2.3 散热器热阻对系统性能的影响

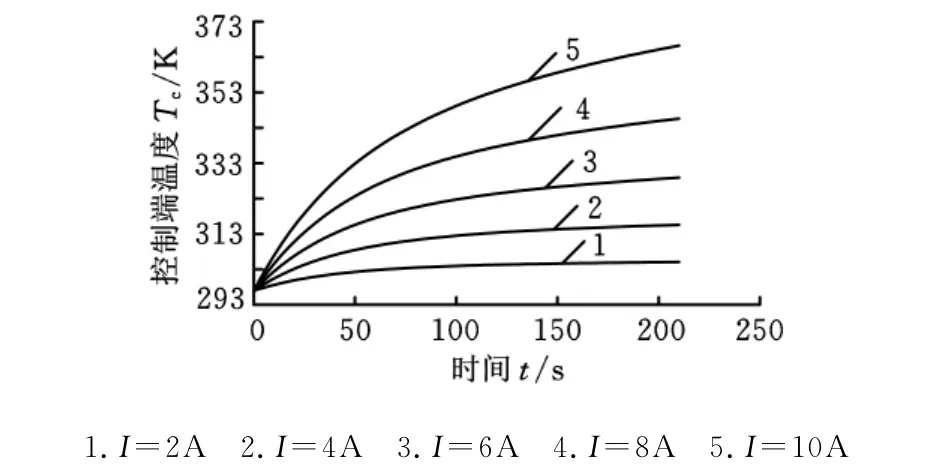
图8 加热模式下不同电流作用下的阶跃响应

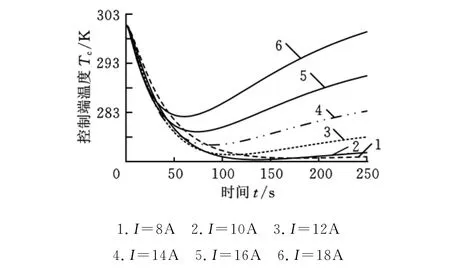
图9 制冷模式下不同电流作用下的阶跃响应

散热器作为热循环系统的重要组成部分，其热阻也是影响系统性能尤其是制冷性能的重要因素。利用系统等效电路模型，可以分析不同的散热器热阻对系统制冷性能的影响。散热器热阻分别为 0.10K／W、0.15K／W、0.20K／W 和 0.25 K／W时的系统稳态特性如图10所示。

图10 不同的散热器热阻时系统的稳态特性

由仿真结果分析可得，较小的散热器热阻在同样大小电流作用下系统能获得更低的温度，具有较高的制冷效率。为此通过改善散热器结构、增加空气流速、增大散热面积等措施，减小散热器热阻，从而提高系统整体性能。

3 结束语

本文在热电制冷器等效电路模型的基础上，建立了PCR仪热循环系统的等效电路模型，通过Multisim10仿真分析了热循环系统在制冷和加热模式下的稳态和动态性能，以及散热器热阻对系统性能的影响。采用该模型进行仿真分析，有助于了解系统特性和闭环控制系统的设计优化。由于系统建模时作了一定简化，忽略了一些因素（如导热硅胶与散热器和热电制冷器之间的接触热阻、热电制冷器安装时产生的附加热阻等）的影响，可通过实验进一步修正模型参数，使仿真结果更加符合实际系统特性。在热循环系统的设计、优化和控制中采用等效电路模型进行分析是一种简单有效的方法。

［1］ Heid C A，Stevens J，Livak K J，et al.Real Time Quantitative PCR［J］.Genome Research，1996，6（10）：986－994.

［2］ 朱冬生，雷俊禧，王长宏，等.电子元器件热电冷却技术研究进展［J］.微电子学，2009，39（1）：94－99.

［3］ Hodes M.On One－dimensional Analysis of Thermoelectric Modules（TEMs）［J］.IEEE Transactions on Components and Packaging Technologies，2005，28（2）：218－229.

［4］ 李曦，曹广益，朱新坚.基于系统辨识的PEMFC温度非线性建模与预测［J］.中国机械工程，2005，16（10）：873－877.

［5］ Chavez J，Ortega J，Salazar J，et al.Spice Model of Thermoelectric Elements Including Thermal Effects［C］／／Proceeding of Instrumentation and Measurement Technology Conference.Baltimore，MD，USA，2000：1019－1023.

［6］ Lineykin S，Yaakov S B.Analysis of Thermoelectric Coolers by a Spice－compatible Equivalent－circuit Model［J］.IEEE Power Electronics Letters，2005，3（2）：63－66.

［7］ Wey T.On the Behavioral Modeling of a Thermoelectric Cooler and Mechanical Assembly［C］／／4th International IEEE North－East Workshop on Circuits and Systems，NEWCAS 2006－Conference Proceedings.Quebec，2006：277－280.

［8］ 聂典，丁伟.Multisim 10计算机仿真在电子电路设计中的应用［M］.北京：电子工业出版社，2009.

［9］ 郑永明，方方，徐建一，等.半导体制冷原理及其应用系统设计研究［J］.中国测试技术，2006，32（2）：49－51.

［10］ 杨明伟，许文海，唐文彦.热电制冷器的等效电路模拟与分析［J］.红外与激光工程，2007（2）：281－285.

［11］ de Baetselier E，Goedertier W，de Mey G.A Survey of the Thermal Stability of an Active Heat Sink［J］.Microelect.Reliab.，1997，37（12）：1805－1812.

Modeling and Analysis of Thermal Cycle System for Quantitative PCR Instrument

Yao Yinghao Chen Zhangwei Huang Jing Liu Juanrong
State Key Laboratory of Fluid Power Transmission and Control，Zhejiang University，Hangzhou，310027

An equivalent circuit model of the thermal cycle system based on thermoelectric cooler was proposed according to the analogy between thermal and electrical variables.The use of this model allows the static and dynamic performance of the system to be analyzed by using electrical circuit analysis programs such as Multisim10.It is an effective and simple method to design，analyze and optimize the thermal electric system by using this model.

quantitative PCR；thermoelectric cooler（TEC）；thermal cycle system；equivalent circuit model

TH79；R318.6

1004—132X（2011）01—0031—04

2010—04—06

（编辑 郭 伟）

姚英豪，男，1984年生。浙江大学流体传动及控制国家重点实验室硕士研究生。研究方向为机电控制。陈章位，男，1965年生。浙江大学流体传动及控制国家重点实验室教授。黄 靖，男，1985年生。浙江大学流体传动及控制国家重点实验室博士研究生。刘娟容，女，1984年生。浙江大学流体传动及控制国家重点实验室硕士研究生。