码头工程空心板安装方案探讨分析

王 矗，张功成

中交第二航务工程局有限公司，湖北武汉 430012

1 工程概况

某有限公司为发展经济，壮大生产规模，拟在长江内侧兴建一座3 000t～5 000t级泊位的进出口仓储码头，码头全长118m，宽18m。码头后方设有引桥两座，布置在上、下游，其中下游引桥长95m，上游引桥长96.72m，桥面宽度均为8m，引桥下部结构为灌注桩基础，上部为梁板式结构。上、下游引桥各14跨，其中江侧两跨为现浇板，预制空心板96块，上、下游引桥各48块，每跨4块。

2 方案比较

第一种方案是在岸侧引桥两侧先铺一层石子便道，用50T履带吊安装。用这种方法保险系数最高，但费用较高，对于一个造价比较低的工程是一个不小的数目。

第二种方案是用“土办法”，把空心板全部倒运在引桥的岸侧（第一跨可以直接安装），在已安板上铺上轨道，然后用卷扬机拉到所安装的前后位置，用葫芦固定左右位置。这种方法虽然费用较低，但进度比较慢，很难满足施工工期要求。

第三种方案是用吊车停靠在已安完的板上，安装下一跨的空心板，考虑到当时板的重量将近10T，经过对吊车的技术参数和现场的考察决定用25T汽车吊。这种方案简单、经济，但保险系数是个未知数，为此，对这种方案进行详细的分析与探讨。

3 第三种方案的分析与探讨

3.1 25T汽车在空心板上行驶和安装的受力分析与计算

考虑25T汽车吊是在安装时的受力情况，以简力板计算。空心板长6.3m，宽2m，高0.45m，搁置长度为0.25m。

3.1.1 汽车吊行驶时跨中最大弯矩的分析与计算

25T汽车吊中后轴间距4.325m为集中荷载，根据25T汽车的质量参数，前轴为P2为3.65T，中后轴为P1为1 0.85T、当中后轴在板中央时为最不利荷载，行驶时跨中受到的最大弯矩为：Mj=M0+Mc1max+Mc2。

式中：

M0为空心板自重荷载产生的跨中弯矩；

Mc1max为汽车吊行驶时产生的跨中最大弯矩；

Mc2为其它变载产生的跨中最大弯矩。

1）M0的计算

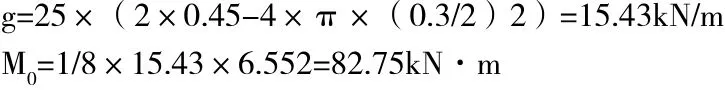
2）Mc1max的计算

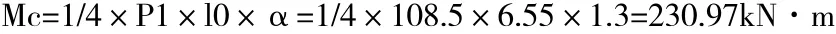
式中：l0为空心板跨距；

α为冲击系数，取1.3。

Mc1max按《高桩码头设计与施工规范》确定相关系数及综合系数后，计算得出。首先确定空心板的抗弯刚度与抗扭刚度比例系数将引桥空心板圆形空心截面转化为矩形空心截面，如图1、2所示，根据面积相等且惯性矩相等的原理得：

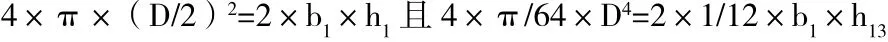
解得b1=544mm，h1=260mm。

3）Mc2的计算

汽车行驶时，其它变载按均载考虑，且假设均载q为5kN/m2，Mc2=1/8×q×l02×α=1/8×5×6.552×1.3=34.86kN·m。经上述计算可得，行驶时跨中受到最大的弯矩为Mj= M0+Mc1max+Mc2=82.75+231.2+34.86=348.81kN·m。

3.1.2 行驶时支座最大剪力计算

支座的剪力由三部分构成，空心板自重产生的支座剪力Q0；汽车行驶时产生的支座剪力Qc1；以及其它变载产生的支座剪力Qc2。

1）Q0的计算：Q0=1/2×15.43×6.3=48.61kN；

2）Qc1的计算：

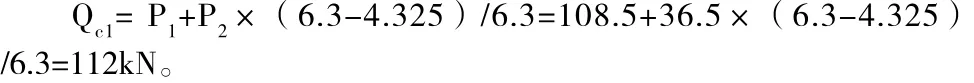
3）Qc2的计算：

其它变载按均载q等于5kN/ m2计，

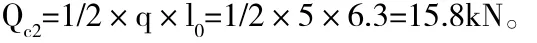
故行驶时支座最大剪力：Qj= Q0+（Qc1max+Qc2）×α=48.61+（112+15.8）×1.3=214.75kN。

3.1.3 安装时受到的最大弯矩计算。

根据《高桩码头设计与施工规范》及汽车吊质量参数，支腿横向跨径5.9m，纵向跨径为2.45m，考虑其受力，汽车吊的荷载集中作用点上布置1m的钢板。由下列数字：a1=b1=1m，a1′=2.08m，b1′=2.45m，la=6.3m，lb=8m进行计算。

3.2 空心板承受安装载荷能力的分析与计算

3.2.1 承受弯矩能力的分析与计算

将圆孔折算成等效矩形孔，然后按T形截面计算。

1）判断T形截面类型

考虑其特殊情况，设砼强度为C20，Ⅱ级钢筋。

Ra=11Mpa，Rg=340Mpa，

配筋为螺纹钢19Φ20，Ag=5 969mm2， ag=5cm，

故属于第Ⅰ类T形截面。

2）计算截面所能承受的最大弯矩

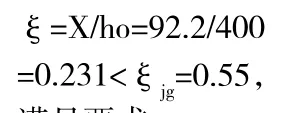
满足要求。

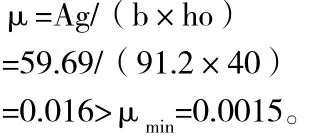
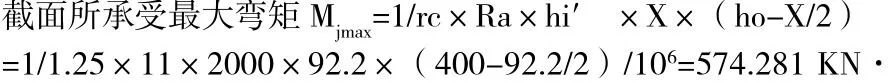
3.2.2 空心板承受剪力能力的分析与计算

空心板的箍筋间距为20㎝，配筋为圆筋5Ф10，ho=45-5=40cm，b=91.2cm，Rl=1.3MPa，

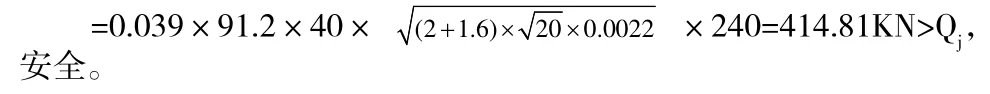
式中：p=100×µ=0.016×100=1.6＜3.5取1.6；

通过对第三种方案的受力分析及计算，可知选用第三种方案是安全可行的。

4 结论

在该工程空心板安装施工中，我们采用了本文论述的第三种方案。这种方案减少了空心板的倒运次数，节省了机械台班费和人工费等，工期不仅有了保障，还比预计提早。整个安装过程没有出现任何安全和质量事故，充分表明这种安装方案是合理的。

[1]高桩码头设计与施工规范（JTj291-98）.