基于蚁群优化算法的线状目标简化模型

郑春燕,郭庆胜,胡华科

1.嘉应学院地理科学与旅游学院,广东梅州514015;2.武汉大学资源与环境科学学院,湖北武汉430079

1 引 言

线状目标的简化一直是地图综合重点研究的问题之一,在经历了几十年的研究和发展后,仍有很多问题没有解决,一方面是由于线状目标简化本身的理论和技术还有待完善、不成熟;另一方面是由于地图空间中线状目标在图形表达上的重要性,线状目标一般要占地图图形的80%以上[1]。从20世纪60年代开始发展至今,已经产生大量较为成熟的算法,如道格拉斯算法、Lang算法、Li-Openshaw算法等[2-3],但不同算法用于线状目标的简化所得结果有差异,说明可行解不唯一,宜将线状目标的简化归结为部分选取的最优化问题[4-7],以获取简化效果最佳的解。

线状目标简化过程中要满足多个相互制约的约束条件,优化方法则可以平衡这些约束条件之间的矛盾[6-7]。整数规划法、遗传算法、最小二乘平差法等的成功应用[4-6],说明优化算法是解线状目标简化问题的一个有效途径。但整数规划法的评价目标是连接数一定的情况下所有连接的偏差之和最小,节点数过于密集则可能保留冗余点[4];遗传算法以所保留的节点数目作为适应度函数的主要矛盾,随着压缩率的增加则可能导致偏移量的增加[5];最小二乘平差法需要建立并解繁多的条件方程,权重设置也较为繁杂[6]。蚁群优化(ant colony optimization,ACO)算法通过模拟自然界蚂蚁搜索路径的方式来解组合优化问题,已经成功应用到旅行商问题、数据挖掘、区位选址等多个领域[8-10]。文献[10]将ACO算法用于河流的符号化和道路网络的专题表达,试验表明相对禁忌搜索算法,ACO算法寻求最优解的搜索效率更高[10]。ACO算法通过蚁群构建的有序路线来获取可行解,其搜索形式同线状目标的简化具有较大的相似性。

本文根据ACO算法的工作原理,提出并验证了顾及节点压缩率和几何精度的线状目标简化模型,主要从目标函数值、几何偏移量、所保留的节点数等方面与道格拉斯算法作了对比分析。

2 多约束条件下线状目标简化的问题描述

约束条件是蚁群构建路径应遵循的规则,满足约束条件的蚂蚁按随机模型确定下次到达的节点。

2.1 约束条件

设原线状目标的节点数为 n个;Xij表示简化后节点i和j是否相邻;Pi表示节点i是否被选取。线状目标简化过程所需要的约束条件主要有:

(1)线状目标的首末端点1和 n必须保留,且都只能与一个节点连接,即

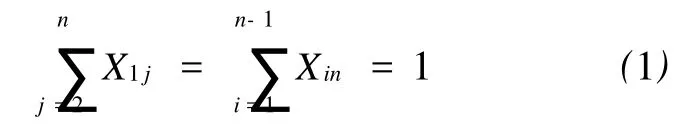
(2)简化后,中间节点 i只能与一个邻近的前继节点和后继节点相连接

(3)简化后,最相邻的两节点才能相连,所以Xij为1的条件是

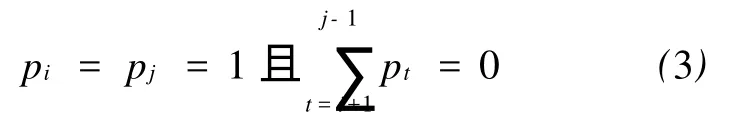
(4)简化后,构成线状目标的每条直线段的矢量偏差Cij要在一定的限差δ范围内,即Cij≤δ。

2.2 随机模型

采用文献[8—9]中近似非确定树搜索中的概率选择方式。位于节点i的蚂蚁k,移动到节点 j的概率由下式给出

式中,ξ是一个参数,取值范围0≤ξ≤1,表示信息素τij和启发式信息ηij的相对影响力;Nki代表了位于节点 i的蚂蚁 k能直接到达的节点的集合。

3 线状目标简化的ACO算法设计

3.1 目标函数

ACO算法利用目标函数值来评价所得解的质量,并进行信息素的更新,使得蚁群向较佳的路线移动。本算法主要从几何精度(矢量偏差、长度偏差等)和节点数来确定目标函数,矢量偏差、长度偏差和所保留节点数的权重为wi、w2和w3

式中,l、n分别为原线状目标的长度和节点个数; lij为节点i和j之间的距离;简化后连接 Xij存在则Xij为1,否则为0;δ表示矢量偏差阈值;w1+ w2+w3=1。

3.2 信息素更新

信息素更新采用正反馈机制,包括信息素的蒸发和释放。节点数越多,则蚂蚁移动到某一节点上的概率越小,信息素的初始值为原线状目标上节点数的平方根的倒数。按基于排列的蚂蚁系统的信息素更新规则来释放信息素,只有排列在最前的(w-1)只蚂蚁和生成了至今最优路径的蚂蚁才允许释放信息素。

3.3 启发式信息

相对目标函数,启发式信息是关于连接的一个局部信息,仍由矢量偏差、长度偏差和所保留的节点数确定。对于未被禁忌的连接 Xij,其启发式信息ηij为

式中,Cij、δ的意义同前;dij为节点i到j的欧氏距离;dmax为可与节点 i建立连接的节点数;Dsij为节点i到j的原线状目标长度。

3.4 长期禁忌表

ACO算法易融入禁忌搜索算法的长期禁忌表vistij,将矢量偏差大于阈值的节点 i和j的对应连接禁忌,以避开一些非可行解。当 vistij的值为true时,表示节点i和j的连接被禁忌。

3.5 局部搜索

当ACO算法与局部搜索相结合时,算法表现出来的性能最好[9]。局部搜索算法能适当局部优化蚂蚁构建的解,提高运算效率。在顾及几何精度的情况下,尽量减少节点数。主要步骤如下:

(1)从当前的路径,依次取三个所保留的节点 i-1、i、i+1,计算连接 Xi-1,i+1的矢量偏差 Ci-1,i+1。

(2)将所求的矢量偏差按从小到大的顺序排列,若最小的矢量偏差大于阈值则转(3);反之,则删除最小矢量偏差所对应的节点 i,并计算舍弃节点i后所得解的目标函数值,返回(1)。

(3)比较由(2)所得目标函数值,以获取局部搜索中的最优解。

3.6 主要运算步骤

(1)初始化ACO所需的几何度量(如线长、矢量偏差等)和参数(蚂蚁数目、信息素蒸发率等)。

(2)构建解。随机选择首末端点作为起点,用m只蚂蚁遍历线状目标上的节点,获得 m个解。

(3)局部搜索。当蚂蚁完成了路径构建后,使用局部搜索进一步优化解。

(4)计算目标函数值,完成信息素的更新。

(5)若不满足终止条件(迭代次数达到最大值等)转步骤(2);否则结束运算,输出最优解。

4 线状目标的简化试验

4.1 试验数据

试验数据为广东省某县第二次全国土地调查成果土地利用数据库系统中的镇级境界线,如图1所示,48个线状目标,一共有43 555个节点,初始比例尺为 1∶10 000,目标比例尺为1∶100 000。

4.2 试验结果分析

本试验中阈值δ为30 m,权重w1和w2分别为0.15和0.1,蚂蚁数量为30,信息素蒸发率ρ为0.2。图2为对图1中红色矩形所标注的境界线简化结果,其中47号为完整显示,21号和31号为局部显示。黑色实线、细虚线分别为ACO算法和道格拉斯算法简化所得,重叠部分为实线,小圆点为原境界线上的节点,灰色区域是以15 m半径为原境界线建立的缓冲区。表1列出了部分试验结果,ID为标识号,K为原有节点数。KA、KD分别为ACO算法和道格拉斯算法所选取的节点数,VA、VD分别为它们所得平均矢量偏差,FA、FD分别为它们所得目标函数值。长度单位为米。

图1 原地图上的镇级境界线Fig.1 The boundary lines of township on initial map

本算法综合考虑了节点数、偏移量等指标,用目标函数值来度量简化效果。由试验结果可知:

(1)由ACO算法与道格拉斯算法所得简化结果都能较有效的逼近原境界线,保留了重要的几何特征点,有良好的外观视觉效果,并取得了较高的压缩率。

(2)比较每条境界线所对应的 FA和 FD,FA值都比 FD值小,VA都比VD小。由目标函数值知,利用ACO算法简化线状目标能得到比道格拉斯算法更好的总体评价效果。

图2 镇级境界线的部分简化结果示意图Fig.2 The schematic diagram of partial simplified result for boundary lines of township

表1 基于ACO算法和道格拉斯算法简化结果对比Tab.1 The comparison on the two simplified results respectively based on ACO algorithmand Douglas algorithm

5 结束语

本文提出的简化线状目标的模型主要顾及了几何精度和节点压缩率,试验表明该模型能取得良好的图形简化效果。有待深入研究的内容主要有:在线状目标简化中顾及空间关系一致性(避免自交、互交等);顾及成组线状目标(如等高线簇)简化后的协调性等。为了使算法更具普适性,还需要针对实际应用中不同语义的线状目标(如水系、道路等)进行大量的研究,以提高算法的性能。

[1] THAPA K.Automatic Line Generalization Using Zero Crossings[J].Photogrammetric Engineering and Remote Sensing,1988,54(4):511-517.

[2] DOU GLAS D H,PEUCKER T K.Algorithms for the Reduction of the Number of Points Required to Represent a Line or Its Caricature[J].The Canadian Cartographer, 1973,10(2):112-122.

[3] GUO Qingsheng,HUANG Yuanlin,ZHENG Chunyan,et al.Spatial Reasoning and Progressive Cartographic Generalization[M].Wuhan:Wuhan University Press,2007. (郭庆胜,黄远林,郑春燕,等.空间推理与渐进式地图综合[M].武汉:武汉大学出版社,2007.)

[4] CROMLEY R G,CAMPBELL G M.Integrating Quantitative and Qualitative Aspects of Digital Line Simplification [J].The Cartographic Journal,1992,29(1):25-30.

[5] WU Fang,DENG Hongyan.Using Genetic Algorithms for Solving Problems in Automated Line Simplification[J]. Acta Geodaetica et Cartographica Sinica,2003,32(4): 349-355.(武芳,邓红艳.基于遗传算法的线要素自动化简模型[J].测绘学报,2003,32(4):349-355.)

[6] HARRIE L,SARJAKOSKI T.Simultaneous Graphic Generallization of Vector Data Sets[J].GeoInformatica,2002, 6(3):233-261.

[7] PUNT E,WATKINS D.User-directed Generalization of Roads and Buildings for Multi-scale Cartography[C]∥Proceedings of 13th ICA Workshop on Generalisation and Multiple Representatio.Zurich:ICA,2010.

[8] DORIGO M,MANIEZZO V,COLORNI A.The Ant System:Optimization by a Colony of Cooperating Agent [J].IEEE Transactions on Systems,Man,and Cybernet: B,1996,26(1):29-41.

[9] DUAN Haibin.Principle and Application of Ant Colony Algorithm[M].Beijing:Science Press,2005.(段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005.)

[10] RICHARDS N,WARE M.Ant Colony Optimization Applied to Map Generalization[C]∥Proceedings of 13th ICA Workshop on Generalisation and Multiple Representation.Zurich:ICA,2010.