富宁县城镇体系空间结构及水系的分形研究

丁贤法

(文山学院生化系，文山云南663000)

分形是城镇体系有效占据空间的重要形式，分形几何理论及其技术已成为通过局部认识整体、从有限认识无限的一种新工具，对地学等自然科学与社会科学都产生了很大的影响，常用来研究形态极不规则的地貌、等高线、水系、断层以及预测地震、水旱等自然灾害等。由于社会经济系统内在的自组织演化以及外在地形、水系等的制约，城镇体系普遍具有分形特征。文章应用GIS数字化了云南省富宁县的扫描地图，计算了该县13个城镇的聚集分维与空间关联分维，同时计算了富宁县那马河水系的分维，并讨论了各种分维对该县城镇化发展的意义。

1 富宁县城镇体系聚集分维研究

假设区域的城镇体系各要素按自相似原则围绕中心城市或首位城市呈凝聚态分布，如果距首位城市平均半径Rs与相应的城镇个数S满足关系:

则区域城镇的分布是分形的，其计算方法陈涛［1］已作了介绍，其中D为分维，D值反映了城镇围绕中心城市随机聚集的特征。当D＜2时，说明城镇分布从中心城市向周围腹地是密度衰减的，中心城市的中心性作用很强;当D=2时，城镇分布在半径方向上是均匀变化的;当D＞2时，说明城镇分布从中心城市向四周是密度递增的，说明中心城市不具备中心性作用，整个体系呈离心状态。

应用MapInfo测量出新华镇至其他城镇的直线距离ri(单位:km，见表1)，计算出富宁县城镇体系的随机聚集分维D=1/0.734 6=1.361 2＜2(见图1)，说明新华镇作为富宁县的政治、经济、文化中心，其中心作用较强，城镇体系要素密度由该镇向四周衰减;新华镇还是滇东南的交通枢纽，有323国道与衡昆高速公路经过，规划目标为:发展生物制品加工和旅游服务、物资集散等第三产业为主，具有壮族民族风情特色的山水城市。观察富宁县城镇体系空间结构的随机聚集分维可知，除里达镇略偏离直线外，各乡镇几乎位于一条直线上，说明目前该县城镇体系的空间结构已趋于最优化的分形结构。

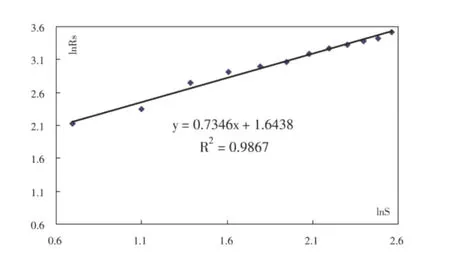
图1 富宁县城镇体系的随机聚集分维

表1 富宁县城镇分布的重心距和平均半径

2 富宁县城镇体系的空间关联分维研究

2.1 城镇体系的空间关联分维计算方法

城镇体系的空间关联函数C(r)定义为

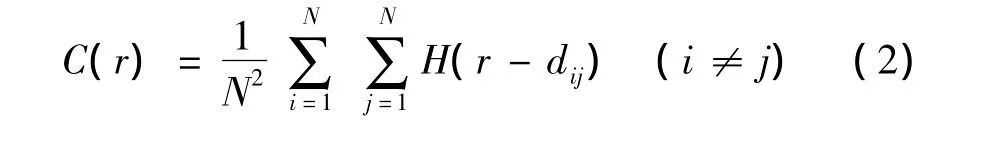
式中N为区域内城镇数目，r为码尺(yardstick)，dij为i、j两城镇的欧氏直线距离，即乌鸦距离(crow distance)，H为Heaviside函数，具有以下性质:

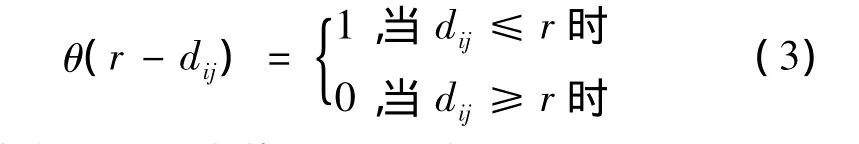
为了计算方便，通常将C(r)改为

如果城镇体系的空间分布是分形的，则应具有标度不变性，即

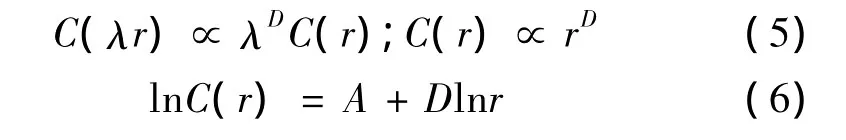
λ为尺度比，D为城镇体系的空间关联维数。D一般在0～2之间变动，当D→0时，表明城镇分布高度集中于一地，形成一个首位城市，但是这种情况很少出现;当D→1时，表明城镇体系各要素集中到一条地理线(如河流、公路、海岸等)上;当D→2时，表明城镇空间分布很均匀。将dij改为实际交通里程，即乳牛距离(cow distance)时，可得城镇交通网络的关联维数D' 。D' 一般在0～2之间变化，D' 越小，表示城镇之间联系越紧密，城镇分布趋于集中;D' 越大，城镇之间相互联系越弱，趋于均匀分布。定义网络直通度(又称牛鸦维数比)为:ρ=D' /D，当ρ＜0.5或ρ＞1时，表明城市之间的网络连通性较差;当0.5＜ρ＜1时，表明城市之间的网络连通性较好;当ρ接近于1，表明城市之间交通趋于直线式通车，ρ=1为极限值［2］。

2.2 富宁县城镇体系的空间关联分维

用MapInfo测量了富宁县13个城镇之间的直线距离，形成一个13×13的矩阵(见表2)，取步长为8 km对其进行筛选，得到一系列点对(r，C(r))(见表3)，将其标绘在双对数坐标图内，进行线性回归计算，发现图中存在明显的无标度区(图2)，对无标度区的点列进行回归运算，得到D=1.297 7，测定系数R2=0.998 3，说明城镇体系趋于线性分布。同理，将表2的直线距离改为交通里程，得到公路交通网络的分维数为D' =1.032 8，测定系数R2=0.994 5。D' 较大，说明城镇之间联系不够紧密;网络直通度为ρ=D' /D=0.796，说明富宁县城镇之间网络联接较好，但有待改进与提高，其主要原因是由于北部乡镇之间缺乏联接，如阿用乡与那能乡直线距离只有31.6 km，却需绕道县城，交通里程达144.6 km。目前，两地之间正在建设一条县级道路。由于323国道与衡阳至昆明高速公路经过，富宁县交通网是比较发达的。

富宁县位于云南省最东部，是云南省通往广西北部湾的公路出海大通道。广西百色水利枢纽竣工后，这里形成了约300 km的优良航道，位于那马河右岸、甲村河左岸河段的富宁港已动工，可沿右江、珠江至港澳，将成为云南省的水路出海通道。

图2 富宁县城镇体系的空间关联分维

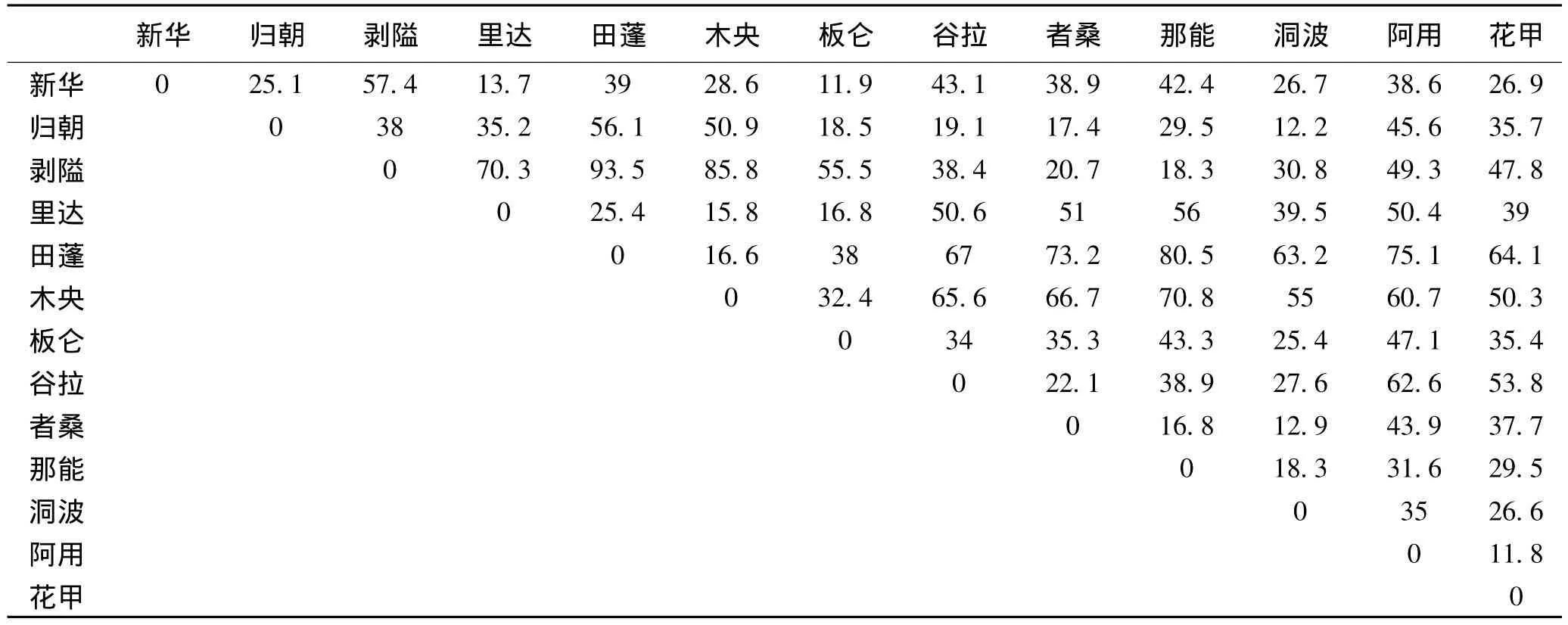
表2 富宁县13个城镇之间的直线距离(单位:km)

3 那马河水系的分维

水系具有典型的分形构造，城镇选址大都受到水系的制约。富宁县水资源丰富，喀斯特地貌发育，水系发达，绝大多数城镇位于水系附近。选取那马河水系，计算其分维。那马河流域干支流水系均位于富宁县境内，且已动工建设的富宁港即位于此。应用MapInfo数字化了该流域水系，输出为AutoCad的 dxf格式［3］，在 ArcView GIS［4］中按一定尺寸(ε，单位:km)将其转为网格(N(ε))，得到表4，计算出其分维为D=1.102 1(见图3)。

图3 那马河水系的分维值

表4 那马河水系的分维值计算

据何隆华等［5］的研究，当水系的分维≤1.6时，流域地貌处于侵蚀发育阶段的幼年期(美国地貌学家戴维斯于19世纪末提出地貌侵蚀循环理论，将流水地表的发育分为幼年期、壮年期和老年期)，水系尚未充分发育，河网密度小，地面比较完整，河流深切侵蚀剧烈，河谷呈V形，这与实际观测较一致。

4 结论与讨论

基于GIS与分形理论，计算了富宁县城镇体系空间结构的聚集分维与关联分维，显示新华镇的中心作用较强，城镇化发展处于极核阶段，在整体上以新华镇为中心的空间结构已趋于最优化的分形结构;受山地地形的制约，富宁县城镇体系趋于线状地理要素分布，主要为公路与河流，文山州［6］、丘北县［7］等城镇体系的空间分布在整体上与此相似。分形研究的结果还显示富宁县交通网络联接较好，那马河水系的分维显示其地形发育处于地貌学家戴维斯提出的侵蚀循环的幼年期。

2006年底，富宁县农业人口占总人口的比例高达93.0%，城镇化水平低，境内山高坡陡，地势狭窄，山区面积占96%，石山区又占山区面积的三分之一，土地资源极为宝贵。因此受地形的制约，“点－轴”系统模式应是统筹城乡一体化发展的最佳空间模式［8－9］，这里的“点”指各级城镇，“轴”指联结点的线状基础设施，主要包括交通干线、高压输电线、通讯线路、供水线路等工程性线路，在城镇的空间拓展、行政区划调整、异地扶贫搬迁中，宜向交通干线、河流聚集，以扩大和发挥城镇的集约与规模效应。例如以323国道与衡昆高速公路沿线为主轴，西部以新华镇为中心，中部以归朝镇为中心，东部以剥隘镇为中心，由主轴线向南北两翼，可划分出若干二级发展轴，特别是新华镇－里达镇－木央－田蓬镇沿线，田蓬镇规划为富宁县城南部区域性中心城镇，是省二级口岸，以发展边境旅游、边贸为主的边境小城镇，可达越南河内、海防，但由于受到西部河口、天保等国家级口岸的空间竞争影响，这条道路等级较低。另外，由于缺乏铁路运输，与同位于东部但位置偏西的曲靖市富源县相比，富宁县还未充分发挥云南省东大门的区位优势，这一局面有望在云桂铁路建成后改变。

最后，由于富宁县地貌发育处于侵蚀循环的幼年期，受山地地形制约，在很长的时间内，城镇化发展都需遵循“点轴”模式。由于乡镇聚落体系与城市体系遵循相同的分形模式［10］，可进一步应用分形研究该县村－镇体系的分形特征。另一方面，地质构造运动可能活跃，需注意防范地震、崩塌、滑坡、泥石流等自然灾害。由于自然灾害的发生在时间轴上表现为一系列的点状事件，类似于分形几何中的康托尔集合(cantor)，因此可以根据历史统计资料，用分形来预测该县未来自然灾害的发生时间和趋势［11］。

［1］陈涛．城镇体系随机聚集的分形研究［J］．科技通报，1995，(2):98 －101．

［2］丁贤法．基于分形理论的云南省文山州城镇体系研究［J］．小城镇建设，2008，(8):101 －103．

［3］朱晓华，查勇．MapInfo与ArcView GIS软件在线体分形分析中的应用［J］．测绘信息与工程，2002，(5):4 －5．

［4］丁贤法．基于ArcView的文山州系列地图制作研究［J］．文山师范高等专科学校学报，2006，(4):92－94．

［5］何隆华，赵宏．水系的分形维数及其含义［J］．地理科学，1996，(2):124 －128．

［6］丁贤法，李巧媛．云南省文山州城镇体系空间结构的分形研究［J］．国土与自然资源研究，2010，(2):20－21．

［7］丁贤法，沐建华，许联芳等．基于Map Info的丘北县城镇分形与辣椒产业发展研究［J］．安徽农业科学，2008，(23):10109－10111。

［8］陆大道．论区域的最佳结构与最佳发展——提出“点－轴系统”和“T”型结构以来的回顾与再分析［J］．地理学报，2001，(2):127 －135．

［9］刘继生，陈彦光，刘志刚．点－轴系统的分形结构及其空间复杂性探讨［J］．地理研究，2003，(4):447－454．

［10］单伟东，陈彦光．信阳地区城乡聚落体系的分形几何特征［J］．地域研究与开发，1998，(3):48～64．

［11］丁贤法，李巧媛，胡国贤．云南省近500年旱涝灾害时间序列的分形研究［J］．灾害学，2010，(2):76 －80．