NCEP、ECMWF及CMC全球集合预报业务系统发展综述

麻巨慧，朱跃建，王盘兴，段明铿

(1.南京信息工程大学气象灾害省部共建教育部重点实验室，江苏南京210044;2.Environmental Modeling Center/NCEP/NOAA，Camp Springs，MD 20746 USA;3.UCAR，Boulder，CO 80307 USA)

0 引言

大气具有混沌特性，对于初始场的微小误差高度敏感，这种误差会迅速增长，影响可预报性(Lorenz，1963)。初始场误差主要来源于观测(资料在时间和空间上的不完整，代表性误差和测量误差等)及资料同化过程(使用背景场误差协方差时假设各向同性及缺乏背景场误差的信息等)，即使假设模式完备，这样的初值也会使预报技巧在几周后降为零(Toth and Kalnay，1993)。况且数值预报模式并非完备，离散化的大气模式仅是真实大气在数学和物理上的近似。有限的模式分辨率、不完备的物理参数化方案及边界条件(近似估计粗糙度长度、土壤湿度、雪盖、植被和海表温度)都会带来模式误差，它像初始误差一样，会影响预报技巧。

集合预报是估计数值预报中不确定性的一种方法，它将单一确定性预报转变为概率预报。初始场的不确定性可用概率密度函数(PDF)来表征。集合预报的初始扰动方法就是通过不同方式取样PDF，包括经典的蒙特卡罗法(Leith，1974)、滞后平均法(Hoffman and Kalnay，1983)、增殖向量法(Toth and Kalnay，1993，1997)、能量模奇异向量法(Buizza and Palmer，1995;Molteni et al.，1996)、观测扰动法(Houtekamer et al.，1996)、集合转换卡尔曼滤波(Bishop et al.，2001;Wang and Bishop，2003)和集合转换法(Wei et al.，2008)等。集合预报不但可以估计初始不确定性，也可以通过采用多模式方法(Houtekamer et al.，1996)、物理过程的随机模拟方法(Buizza et al.，1999)及随机全倾向扰动法(Hou et al.，2006，2008，2010)等来捕捉与模式相关的不确定性，从而弥补单一确定性预报的不足。

集合预报可以通过追踪初始不确定性的时空演变，提供依流型(flow-dependent)的概率分布，来提高可预报性(Toth et al.，2007)。不同用户在根据集合预报结果进行决策时要比使用单一预报得到更多的经济利益，因为集合预报可以针对他们各自的成本/损失比提供不同的决策标准(Zhu et al.，2002)，而单一确定性预报无法帮助每一个用户根据自身的情况做出最优的决策，用户只能简单地依赖气候场信息进行判断。Joslyn et al.(2007)和Nadav-Greenberg and Joslyn(2009)的研究表明，预报中包含不确定性估计，可以帮助预报员和公众做出更好的决策。

美国国家环境预报中心(National Centers for Environmental Prediction，NCEP)和欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts，ECMWF)于1992年12月分别建立了各自的全球集合预报系统(global ensemble forecast system，GEFS)，加拿大气象中心(Canadian Meteorological Centre，CMC)的集合预报业务也于1998年2月建成，它们是目前最具代表性的GEFS，ECMWF和CMC称其为GEPS(global ensemble prediction system)，为叙述方便，本文统一称为GEFS。近来一些研究也对这3个中心的初始扰动方法及集合预报产品进行了比较。Bowler(2006)使用低阶的Lorenz 96模式比较得出集合卡尔曼滤波(ensemble Kalman filter，EnKF)方法要优于增殖向量(breed vector，BV)法和奇异向量(singular vector，SV)法的结论，Descamps and Talagrand(2007)也使用Lorenz 96模式和三层准地转模式得到了一致的结论。尽管上述试验在比较中基于相同的模式，避免了模式差异对比较结果的影响，但模式过于简单，尚不能代表复杂的大气系统。Magnusson et al.(2008)使用TL255L40的ECMWF集合预报模式比较了SV法和BV法，发现在热带外地区SV方法的表现稍好，在热带地区则反之。Buizza et al.(2005)比较了3个中心2002年5—7月20～80°N 500 hPa位势高度场集合预报产品，总体而言，ECMWF表现最好，NCEP在短预报时效效果好，CMC对长预报时效效果好。WMO(World Meteorological Organization)的THORPEX(the observing system research and predictability experiment)科学计划中的TIGGE计划(the THORPEX interactive grand global ensemble)提出了建立全球交互式大集合预报的思路，TIGGE资料的交换为各中心预报产品的比较、自身技术的改进提供了有价值的信息。

10余年来，3个中心的GEFS都有了明显的改进，本文第1节将介绍有关3个中心GEFS的发展概况，第2、3节分别介绍3个中心如何估计初值和模式不确定性，第4节是关于建立多模式、多中心集合预报系统的进展情况，第5节是对本文的总结。

1 发展概况

表1、2、3列出了3个中心的详细发展概况。自GEFS开始业务化以来，3个中心就在不断地致力于发展和完善初始和模式扰动方法，同时模式分辨率、集合成员数及预报时效也都有所升级。

ECMWF最初每周仅进行3次业务预报(周五、六、日，12时(世界时，下同)起始预报)，使用T63L19(水平分辨率约219 km)对32个集合成员积分10 d。到目前已经升级为包括50个集合成员，每天两次(00时、12时)，使用可变分辨率GEFS模式进行15 d预报，即0～10 d预报运行高分辨率模式TL639L62(约30 km)，10～15 d预报改用TL319L62(约65 km)。

NCEP的GEFS建成之初，在每天00时仅由1组正负扰动对产生2个集合成员。目前集合成员数已增到20个，每天00、06、12和18时起报，预报时效达16 d，水平分辨率于2010年2月升级为T190(约70 km)。

CMC的第1代GEFS仅使用TL95 SEF模式(spectral finite element model)对8个集合成员积分10 d。1999年8月新开发了GEM(global environmental multiscale model)，由模式中不同的物理参数化方案产生了另外8个成员，模式的分辨率是1.875°。2007年7月CMC对GEFS进行了一次重要的升级，不再使用SEF模式，并将GEM的水平分辨率提高到0.9°，对20个集合成员进行16 d预报。

图1a比较了3个中心集合预报的距平相关系数，每个中心都只取10个集合成员进行集合平均，其中ECMWF的预报效果最好，NCEP次之。但ECMWF的这种优势在一定程度上取决于较高的模式分辨率。如要比较仅由初始和模式扰动方法提高的预报技巧，可由图1b中集合平均与控制预报的差来反映，在预报时效小于3 d时，3个中心的预报效果基本相当，之后CMC开始显现优势，CMC的多参数化方案更好地代表了模式不确定性，体现了其优越性。

表1 ECMWF GEFS发展概况Table 1The development of the ECMWF GEFS

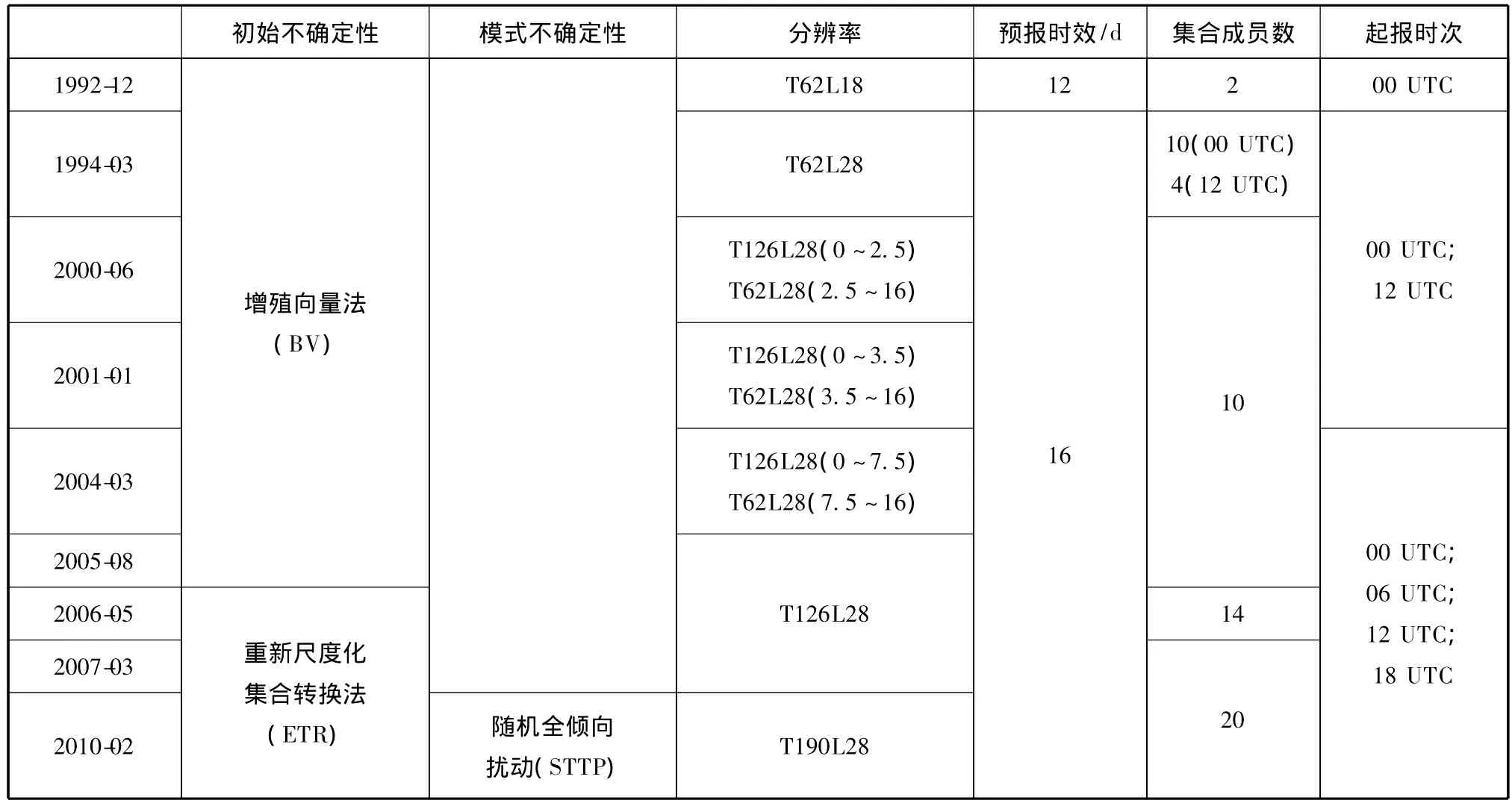
表2 NCEP GEFS发展概况Table 2The development of the NCEP GEFS

表3 CMC GEFS的发展概况Table 3The development of the CMC GEFS

2 初值不确定性

1)ECMWF

根据非线性动力学的有限时间不稳定理论，扰动在相空间的不同方向具有不同的增长率。基于这一原理，ECMWF使用奇异向量(SV)法来捕捉扰动增长最快的方向(Buizza and Palmer，1995;Molteni et al.，1996)(由于这种SV是生成在预报的初始时刻，为区别于其他SV，以SVINI(initial time SV)来表示)。SVINI是相对于初始模定义的，它是通过在最优时间内向前积分切线性模式，再向后积分伴随模式，得到在最优间隔内能够达到极大能量增长的扰动，因此初始模的选取和最优间隔的长度很关键，ECMWF业务上使用总能量模作为初始模，最优间隔最初是36 h，1994年后更新为48 h。得到的SVINI在相空间中再进行正交旋转及重新尺度化构造集合扰动成员。由于使用切线性模式和其伴随模式的次数是所需奇异向量数的3倍，因此需要耗费大量的计算资源，所以仅运行T42的低分辨率模式。对于热带外地区，两个半球是分别计算奇异向量的，否则会使夏半球的奇异向量过少。在热带地区，奇异向量对切线性模式中非绝热物理过程很敏感，如果计算整个热带地区的奇异向量，有时会生成在非线性预报模式中不增长的虚假结构，所以仅计算热带气旋附近区域的奇异向量(Barkmeijer et al.，2001)。为了提高短期集合预报的技巧，1998年3月ECMWF提出了演化奇异向量法(evolved SV-initial time SV，EVO-SVINI)，将SVINI与演化了48 h的SV按一定的权重合并，这样一定程度上代表了资料同化循环引起的初始不确定性增长，得到了很好的效果(Barkmeijer et al.，1998)。

图1 2008年12月1日00时—2009年2月28日00时(世界时)北半球500 hPa位势高度场的距平相关系数(a;实线为集合平均预报，虚线为控制预报)以及集合平均预报与控制预报距平相关系数之差(b)Fig.1 500 hPa geopotential height over the Northern Hemisphere extra-tropics for the winter of 2008—2009a.anomaly correlation scores(solid lines are ensemble mean;dash lines are control forecast);b.differences of anomaly correlation scores between the ensemble mean and the control forecast

2010年6月ECMWF开始采用集合资料同化—奇异向量法(ensemble of data assimilation-initial time SV，EDA-SVINI)(Buizza et al.，2008，2010)。EDA扰动由扰动观测场、海表温度场以及物理过程中的参数化倾向得到。因为演化的SV与EDA扰动都是用来估计资料同化过程中带来的初始不确定性增长，但EDA较前者效果更好，所以用其取代演化的SV。EDA扰动与未受扰动的分析场相加，可生成10个扰动分析场，然后分别与5个SVINI合并，可得到50个集合成员，其中由于EDA扰动的振幅比原来的演化SV大，所以合并时SVINI的振幅降低10%。Palmar et al.(2007)和Buizza et al.(2008，2010)研究表明，只使用EDA扰动代表初始不确定性，误差增长很慢，集合离散度太小，尤其是在热带外地区，影响了预报效果。但与SVINI合并后，与EVO-SVINI相比，在热带以外地区预报时效的前2 d和热带地区的前10 d，EDA-SVINI都具有更大的离散度，之后二者基本相当。

2)NCEP

Toth and Kalnay(1993，1997)设计了增殖向量(BV)法，并于1992年在NCEP投入业务使用。该方法引入初始随机扰动后，经过3～4 d的增殖循环产生具有极大增长率的扰动，然后通过重新尺度化使慢速增长型误差比重减小，得到最终的初始扰动场。BV法的局限性在于，初始扰动方差是由不随时间变化的气候场分析误差限定的，另外扰动之间并未接近正交。

集合转换(ensemble transform，ET)和重新尺度化集合转换(ensemble transform with rescaling，ETR)技术是对BV法的改进，最早是Bishop and Toth(1999)在目标观测研究中提出的。2004年之前NCEP就开始了ET和ETR生成集合预报初始扰动的试验，2006年5月ETR正式在NCEP投入业务使用。该方法产生的初始扰动受业务资料同化(data assimilation，DA)系统提供的分析场误差方差限定，并以DA提供的分析场为中心，同时GEFS也为DA提供预报场误差协方差，因此在ET和ETR方法中GEFS和DA具有一致性，这是原始的BV方法不具备的。另外各扰动之间接近正交，即相关性很小。所以ET和ETR方法弥补了BV正负扰动对方法中的一些不足(Wei et al.，2006)，但却保留了BV法依流型变化、代表误差最快增长的非线性扰动及耗用计算资源少的优点。

ETR方法(Wei et al.，2008)主要是通过集合转换矩阵T将预报场扰动Zf转换为分析场扰动Za:理想的初始扰动应该是中心化的，这样才能以最可能的分析场为中心，从而得到最优的集合平均;另外还应具有最大的自由度，在集合子空间中分布到尽量多的方向上。通过方程(1)的转换各扰动间相互正交，但并未中心化。因此还要进行中心化处理，但这又使各扰动间不再严格的正交，不过可证明集合成员越多扰动间越接近正交。另外，为了使初始离散度分布能与分析误差方差相似，还需要做重新尺度化。

综上所述，经过ETR转换之后的分析扰动具有如下性质:1)各扰动之间以分析场为中心;2)成员越多，各扰动间越接近正交;3)具有最大的自由度;4)具有依流型变化的空间结构;5)如果集合成员数越多，初始扰动的协方差与DA提供的分析场误差协方差越一致。Wei et al.(2008)比较了分别由BV、ET、ETR和ETKF(ensemble transform Kalman filter)产生初始扰动的集合预报，在大多数评分中ETR的表现最好。Magnusson et al.(2009)使用了相同的模式和4D-Var DA系统，比较ETR和SV的预报技巧，经统计，文中19项比较，ETR优于SV的占13项。

3)CMC

观测扰动法(perturbed-observation，PO)(Houtekamer et al.，1996)，以随机扰动法(Monte Carlo)为基础。具体做法是:首先对观测场加随机扰动，将扰动的观测场与上一循环提供的预报场一起进行资料同化，得到扰动的分析场。然后用扰动的预报模式对这个分析场积分6 h，得到下一同化循环的预报场。循环4 d之后，集合统计量达到稳定，最终得到可用于中期预报的扰动分析场。这种初始扰动方法计算量小，且估计了分析误差，但在随机取样时会引入了不增长误差，影响预报在短期的效果。

2005年1月，CMC开始使用集合卡尔曼滤波(EnKF)(Houtekamer and Mitchell，2005;Houtekamer et al.，2007)为集合预报提供初值。这种方法将资料同化与集合预报相结合，在计算时不仅不要求使用复杂的切线性和伴随模式，而且可以得到集合预报提供的随天气形势演变的背景场误差协方差。但是业务运行结果表明得到的分析场离散度太小，这是因为EnKF方法计算过程中，增益算子和分析误差都来自于具有单一集合框架的有限的集合成员，因此低估了分析不确定性，使随后的集合预报离散度偏小。2007年7月CMC就这一问题对EnKF方法进行了改进，将96个集合成员分成了4个子集合(每组24个成员)，在同化任一组观测场时，使用由另3组72个成员计算得到的增益算子。由于每个子集合中各成员间统计量差异并不大，只从每组中各选出5个，共形成20个成员用于中期预报的初始场。在初始时刻还需加入随机扰动，扰动的平均振幅要接近原始EnKF分析场成员的离散度，这样可以弥补在初始阶段集合离散度增长不够的问题。这种集合预报与资料同化相结合的初始扰动方法，不但可以为集合预报提供能够代表分析不确定性的最优初值，同时集合预报又可以为同化提供尽可能准确的背景场误差协方差估计。

3 模式的不确定性

1)ECMWF

1998年10月ECMWF开始在业务集合预报中考虑模式不确定性，使用随机参数化扰动方案(stochastic perturbed parameterization tendencies，SPPT)(Buizza et al.，1999，Palmer et al.，2009)，对物理参数化过程中的敏感因子进行扰动，即在次网格尺度物理参数化生成的总倾向上乘以一个在［－0.5，0.5］范围内均匀分布的随机数，可表示为

式中:Xc为未经扰动的倾向;Xp为扰动后的倾向;rX为随机数。不同的变量rX取值不同，但对于每一个扰动变量，为了保持空间和时间上的连续性，随机数rX在每个10°×10°的整层大气区域内，每6个时间积分步长(对应TL399的3 h，TL215的4.5 h)里，取值不变。这种方案可以增加集合离散度，提高概率预报的技巧，但集合的发散度仍偏小。

2009年9月ECMWF对SPPT方法进行了修订(Palmer et al.，2009)，将方程(2)改写为

其中μ∈［0，1］用来减小近地面和平流层扰动振幅。因为对底层大气进行扰动会引起模式不稳定，而平流层的倾向以辐射强迫为主，它在平流层相对准确，误差主要是大尺度的，所以修订后的SPPT方法中低于300 m和高于50 hPa时不加扰动。此外，这里的随机数r服从高斯分布，所有变量的r都取相同值，这样使模式的物理过程更加具有一致性。与原始的SPPT方法相比，修订后降水预报和热带地区的预报效果有所改善。

下面介绍随机补偿方案(spectral stochastic backscatter scheme，SPBS)(Shutts，2004，2005;Berner et al.，2009)。与真实大气相比，全球天气预报模式中的模式大气在截断尺度附近会出现能量的过度耗散，这种数值过程的耗散会抑制能量从次网格尺度向可分辨尺度的转换。同样，参数化的次网格重力波倾向和深对流也影响这种能量转换。SPBS方案则通过流函数强迫项Fψ来补偿这种耗散。ECMWF通过了此方案的测试，于2010年11月将其与修订的SPPT算法一同用于代表业务集合预报系统中模式的不确定性。

2)NCEP

NCEP从2010年2月起使用随机全倾向扰动法(stochastic total tendency perturbation，STTP)(Hou et al.，2006，2008，2010)，在模式方程的倾向T中加入了随机强迫项S，来代表与模式相关的不确定性。即用

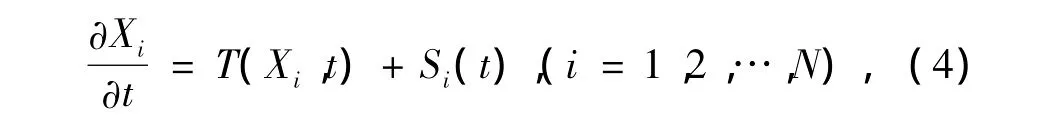
代替传统的模式方程

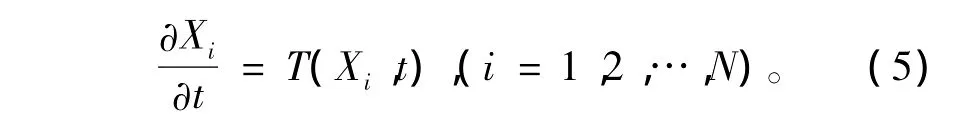
假设任一集合成员的倾向可以代表未知的真实的倾向，则真实的倾向值与传统的模式方程的差别，即每个成员与控制预报倾向的差，为N个扰动:

虽然随机选取的每个Pi都可以用来代表倾向中的不确定性，但如果将N个倾向扰动随机合并起来，则可以代表位相空间中更多的方向，会有更好的效果。因此随机强迫项可以表示为

其中wi，j为每个集合成员i对应的不同的一组随机权重。对于任一成员i的权重wi，j(j=1，2，…，N)是由初始t=0时随机产生的正交矩阵，之后随时间变化不断的旋转一个微小的角度，形成新的正交矩阵。同时P也是正交的，因此得到的S同样是正交矩阵。由于计算资源的限制，不可能每一积分步对倾向加一次随机扰动，只能对一个固定的时间间隔Δt进行，因此模式中积分的状态变量改写为

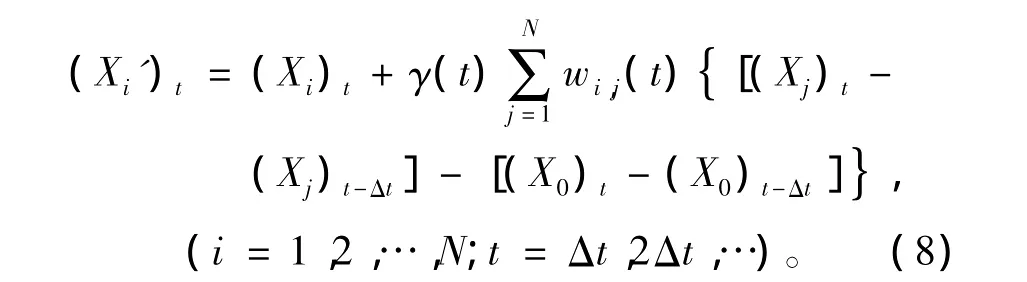
其中γ(t)为全球重新尺度化因子，用来降低随机强迫项的振幅。每个成员的随机强迫为

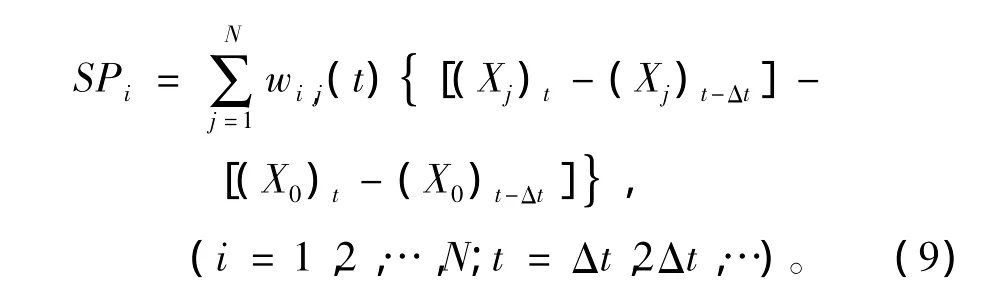
试验表明，STTP可以增加集合离散度，减少集合平均预报中的系统误差。

3)CMC

CMC使用多模式多参数化方案代表模式不确定性(multi-model and multi-parameterization)(Houtekamer et al.，1996)。在2007年7月之前使用GEM(Cote et al.，1998)和SEF(Ritchie and Beaudoin，1994)两种模式分别生成8个集合成员，各集合成员具有不同的水平扩散、对流、辐射、陆面过程和重力拖拽等物理参数化方案。然而数值预报模式的版本和参数化方案的数量毕竟有限，因此这种代表模式不确定性的方法具有一定的局限性。而且近些年SEF模式的发展水平已经远不及GEM模式，它所生成的8个集合成员的预报技巧明显低于GEM模式生成的8个成员。因此从2007年7月开始CMC GEFS仅使用GEM一个模式，多参数化方案依然采用，但更新为20组不同的参数化方案，同时又使用了随机参数化扰动方案(SPPT)和随机动能补偿方案(stochastic kinetic energy backscatter，SKEB)两个随机参数化过程，共同来代表模式相关的不确定性(Charron et al.，2010)。

4 多中心多模式集合预报系统

世界各国各地区的环境预报中心都在致力于提供可靠、及时、准确的预报及预警，以满足人们日益增长的对环境信息的需求(朱跃建，2010)。在过去的十几年间，集合预报技术得到了发展(段明铿和王盘兴，2004;关吉平等，2006)，促进了极端天气和高影响天气预警能力的提高。旨在加快提高1～14 d高影响天气预报准确率的THORPEX国际研究计划将TIGGE计划列为其主要部分(Richardson et al.，2005;Bougeault et al.，2010)。2005年启动的TIGGE计划主要目的是增强国际间对多模式/多分析集合预报的合作研究，并结合用户对预报信息的需求，将其应用到高影响天气预报中。目前由澳大利亚、巴西、法国、韩国、加拿大、美国、欧洲中期天气预报中心、日本、英国和中国的10个业务或准业务GEFS向TIGGE资料库提供预报资料，为研究比较各系统的预报技巧及构建最优的多模式集合提供了便利条件(智协飞和陈雯，2010)。Park et al.(2008)应用TIGGE资料比较了单个和多模式GEFS，结果显示对于北半球500 hPa位势高度场多模式预报较单个GEFS稍有提高，对热带850 hPa温度场提高很明显。Johnson and Swinbank(2009)研究了ECMWF、NCEP和UKMO(United Kingdom Met Office)组成的三模式集合预报的预报效果，发现它比单个集合预报有显著的提高，尤其是2 m温度场。Titley et al.(2008)将多模式集合应用到一次热浪的个例中，得到了与Johnson and Swinbank(2009)类似的结论。这些成果说明了基于TIGGE资料的研究能够帮助我们更好地理解目前各中心使用的扰动方法在集合预报中的表现，并提高多模式集合预报的效果。

中国气象局(China Meteorological Administration，CMA)作为TIGGE资料全球3个交换中心之一，充分利用获取的大量TIGGE资料进行科学研究(Jiao，2010)，主要包括进行集合转换(ET)初值扰动技术和数值模式不确定性的研究、发展多中心多模式超级集合预报产品的集成和应用技术以及建立以集合预报技术为基础的气象水文风险预报模型。已得到了一些初步的研究成果，如智协飞等(2009)基于TIGGE资料中的ECMWF、JMA(Japan Meteorological Agency)、NCEP和UKMO四个中心北半球中纬度地区地面气温集合预报资料进行了超级集合试验。赵晓琳等(2010)基于TIGGE资料，分析了集合变换卡尔曼滤波适应性观测敏感区识别方法在实际应用中的具体环节。

加拿大、墨西哥和美国于2004年建立了北美集合预报系统(North American ensemble forecast system，NAEFS)(Toth et al.，2005)，目前美国海军舰队数值大气海洋中心(Fleet Numerical Meteorology and Oceanography Center，FNMOC)正准备加入，英国(UKMO)和中国(CMA)也有计划考虑在未来加入。这是一个业务化的多中心多模式GEFS，主要进行的工作包括:交换原始预报数据(加拿大和美国各20个集合成员的预报)，对所有成员进行后处理，然后合并所有集合成员得出最终的预报产品。图2比较了NCEP和CMC各20个经过偏差订正后的集合成员，及合并后的40个NAEFS成员的CRPSS(continuous ranked probability skill score)检验评分，它可以度量集合预报的可靠性(reliability)和分辨能力(resolution)(Zhu et al.，1996)，可以看出NCEP和CMC预报效果比较匹配，合并后的NAEFS预报技巧提高明显，尤其在长预报时效时。Zhu and Toth(2008)对2006/2007年冬季的预报效果检验也得到了同样的结果。NAEFS与TIGGE计划有着紧密的联系，NAEFS需要应用TIGGE的研究成果来进一步发展，同时又为建立全球多模式集合预报系统提供了业务框架，这两个计划最终将合并为一个业务系统—全球交互式预报系统(global interactive forecasting system，GIFS)，以提高对全球高影响天气的预报和预警能力。

5 结论

集合预报已成为当今一种重要的预报技术被全球多个国家和地区的业务和研究中心所使用，尤其是用于提高对高影响天气的预警。本文总结了目前最具代表性的3个GEFS——NCEP、ECMWF和CMC建成至今的发展概况。由于计算资源的不断扩展，各中心集合预报系统的模式分辨率、集合成员数也随之增加。如何利用有限的计算资源，实现最优的预报效果，选取模式分辨率和集合成员数的最佳组合尤为关键。同时各中心都在不断地致力于发展和完善初始和模式扰动方法。其中初始扰动方法从最初的增殖向量法(NCEP)、奇异向量法(ECMWF)、观测扰动法(CMC)更新为现在的重新尺度化集合转换法(NCEP)、集合资料同化—奇异向量法(ECMWF)和集合卡尔曼滤波(CMC)，发展与资料同化相结合的初始扰动方法也将成为未来估计初始不确定性的主要研究方向。对于与模式有关的不确定性，ECMWF和CMC都修订了各自的随机参数化方案和多参数化方案，NCEP最近也在模式中加入了随机全倾向扰动。

图2 2008年12月1日00时—2009年2月28日00时(世界时)北半球500 hPa位势高度场集合预报的CRPSSFig.2 CRPSS for 500 hPa geopotential height over the Northern Hemisphere extra-tropics for the winter of 2008—2009

多模式、多中心集合预报是减少模式系统误差的有效方法，试验表明预报效果相匹配的模式组合可以有效地提高预报技巧。旨在提高1～14 d高影响天气预报准确率的TIGGE计划，增进了国际间对多模式、多分析集合预报的合作研究，为建立全球多模式集合预报系统提供了理论基础，北美集合预报系统(NAEFS)则可以为其提供业务框架，这都将有助于未来全球交互式业务预报系统的构建。

中国GEFS的技术水平也在不断的提高(付顺旗和张立凤，1999;李泽椿和陈德辉，2002;金荣花等，2007)，尤其在TIGGE计划的推动下，2006年CMA开始业务运行的以增殖向量法为初始扰动方法的T213L31全球模式集合预报产品也被列入TIGGE交换资料之中，另外在初始扰动方法、模式误差增长的机理和特征等方面都开展了深入的研究，并建立了基于TIGGE资料的中国强天气识别方法以及交互式致洪暴雨预报模型。

致谢:在本文完成过程中，美国国家环境预报中心侯定臣博士和魏谟政博士给予了热情帮助和精心指导，在此表示感谢!

段明铿，王盘兴.2004.集合预报方法研究及应用进展综述［J］.南京气象学院学报，27(2):279-288.

付顺旗，张立凤.1999.中期数值天气预报业务的回顾与展望［J］.气象科学，19(1):104-110.

关吉平，张立凤，张铭.2006.集合预报研究现状与展望［J］.气象科学，26(2):228-235.

金荣花，田伟红，矫梅燕.2007.基于Ward聚类法的中国业务集合预报系统的产品开发［J］.气象，33(12):9-15.

李泽椿，陈德辉.2002.国家气象中心集合数值预报业务系统的发展及应用［J］.应用气象学报，13(1):1-15.

赵晓琳，朱国富，李泽椿.2010.基于TIGGE资料识别适应性观测敏感区的应用研究［J］.应用气象学报，21(4):405-415.

智协飞，林春泽，白永清，等.2009.北半球中纬度地区地面气温的超级集合预报［J］.气象科学，29(5):569-574.

智协飞，陈雯.2010.THORPEX国际科学研究新进展［J］.大气科学学报，33(4):504-511.

朱跃建.2010.预报科学［J］.大气科学学报，33(3):266-270.

Barkmeijer J，Van Gijzen M，Bouttier F.1998.Singular vectors and estimates of the analysis error covariance metric［J］.Quart J Roy Meteor Soc，124:1695-1713.

Barkmeijer J，Buizza R，Palmer T N.2001.Tropical singular vectors computed with linearized diabatic physics［J］.Quart J Roy Meteor Soc，127:685-708.

Berner J，Shutts G J，Leutbecher M，et al.2009.A spectral stochastic kinetic energy backscatter scheme and its impact on flow-dependent predictability in the ECMWF ensemble prediction system［J］.J Atmos Sci，66:603-626.

Bishop C H，Toth Z.1999.Ensemble transformation and adaptive observations［J］.J Atmos Sci，56:1748-1765.

Bishop C H，Etherton B J，Majumdar S.2001.Adaptive sampling with the ensemble transform Kalman filter.Part I:Theoretical aspects［J］.Mon Wea Rev，129:420-436.

Bowler N E.2006.Comparison of error breeding，singular vectors，random perturbations and ensemble Kalman filter perturbation strategies on a simple model［J］.Tellus，58A:538-548.

Buizza R，Palmer T N.1995.The singular-vector structure of the atmospheric global circulation［J］.J Atmos Sci，52:1434-1456.

Buizza R，Miller M，Palmer T N.1999.Stochastic representation of model uncertainties in the ECMWF ensemble prediction system［J］.Quart J Roy Meteor Soc，125:2887-2908.

Buizza R，Houtekamer P L，Toth Z，et al.2005.A comparison of the ECMWF，MSC，NCEP global ensemble prediction systems［J］.Mon Wea Rev，133:1076-1097.

Buizza R，Leutbecher M，Isaksen L.2008.Potential use of an ensemble of analyses in the ECMWF ensemble prediction system［J］.Quart J Roy Meteor Soc，134:2051-2066.

Buizza R，Leutbecher M，Isaksen L，et al.2010.Combined use of EDA-and SV-based perturbations in the EPS［J］.ECMWF Newsletter，123:22-28.

Bougeault P，Toth Z，Bishop C，et al.2010.The THORPEX interactive grand global ensemble(TIGGE)［J］.Bull Amer Meteor Soc，91:1059-1072.doi:10.1175/2010BAMS2853.1.

Charron M，Pellerin G，Spacek L，et al.2010.Towards random sampling of model error in the Canadian ensemble prediction system［J］.Mon Wea Rev，138(5):1877-1901.doi:10.1175/2009MWR3187.1.

Cote J，Gravel S，Methot A，et al.1998.The operational CMC-MRB global environmental multiscale(GEM)model.Part I:Design considerations and formulation［J］.Mon Wea Rev，126:1373-1395.

Descamps L，Talagrand O.2007.On some aspects of the definition of initial conditions for ensemble prediction［J］.Mon Wea Rev，135:3260-3272.

Hoffman N，Kalnay E.1983.Lagged averaged forecasting，an alternative to Monte Carlo forecasting［J］.Tellus，35A:100-118.

Hou D，Toth Z，Zhu Y.2006.A stochastic parameterization scheme within NCEP global ensemble forecast system［C］∥Extended abstract，the 18th AMS conference on probability and statistics，29 January—2 February 2006，Atlanta，Georgia.

Hou D，Toth Z，Zhu Y，et al.2008.Impact of a stochastic perturbation scheme on NCEP global ensemble forecast system［C］∥Extended abstract，the 19th AMS conference on probability and statistics，21—24 January 2008，New Orleans，Louisiana.

Hou D，Toth Z，Zhu Y，et al.2010.A stochastic total tendency perturbation scheme representing model-related uncertainties in the NCEP global ensemble forecast［J］.Submitted to Tellus.

Houtekamer P L，Lefaivre L，Derome J，et al.1996.A system simulation approach toensemble prediction［J］.MonWea Rev，124:1225-1242.

Houtekamer P L，Mitchell H L.2005.Ensemble Kalman filtering［J］.Quart J Roy Meteor Soc，131:3269-3289.

Houtekamer P L，Charron M，Mitchell H L，et al.2007.Status of the global EPS at environment Canada［R］∥Proc ECMWF workshop on ensemble prediction，7—9 November 2007，ECMWF，Shinfield Park，Reading，Berkshire RG2 9AX，UK，57-68.

Jiao M.2010.Progress on the key technology development in application of ensemble prediction products associated with TIGGE［J］.Acta Meteor Sinica，68:136.

Johnson C，Swinbank R.2009.Medium-range multi-model ensemble combination and calibration［J］.Quart J Roy Meteor Soc，135:777-794.

Joslyn S，Pak K，Jones D，et al.2007.The effect of probabilistic information on threshold forecasts［J］.Wea Forecasting，22:804-812.

Leith C E.1974.Theoretical skill of Monte Carlo forecasts［J］.Mon Wea Rev，102:409-418.

Lorenz E N.1963.Deterministic non-periodic flow［J］.J Atmos Sci，20:130-141.

Magnusson L，Leutbecher M，Kallen E.2008.Comparison between singular vectors and breeding vectors as initial perturbations for the ECMWF ensemble prediction system［J］.Mon Wea Rev，136:4092-4104.

Magnusson L，Nycander J，Kallen E.2009.Flow-dependent versus flowindependent initial perturbations for ensemble prediction［J］.Tellus，61A:194-209.

Molteni F，Buizza R，Palmer T N，et al.1996.The ECMWF ensemble prediction system:Methodology and validation［J］.Quart J Roy Meteor Soc，122:73-119.

Nadav-Greenberg L，Joslyn S.2009.Uncertainty forecasts improve decision-making among non-experts［J］.Journal of Cognitive Engineering and Decision Making，3:209-227.

Palmer T N，Buizza R，Leutbecher M，et al.2007.The ensemble prediction system-recent and ongoing developments［R］∥ECMWF tech.memo.no.540，ECMWF，Shinfield Park，Reading，Berkshire RG2 9AX，UK.

Palmer T N，Buizza R，Doblas-Reyes F，et al.2009.Stochastic parametrization and model uncertainty［R］∥ECMWF tech.memo.no.598，ECMWF，Shinfield Park，Reading，Berkshire RG2 9AX，UK.

Park Y-Y，Buizza R，Leutbecher M.2008.TIGGE:Preliminary results on comparing and combining ensembles［J］.Quart J Roy Meteor Soc，134:2029-2050.

Richardson D，Buizza R，Hagedorn R.2005.Final report of the 1st workshop on the THORPEX interactive grand global ensemble(TIGGE)［C］∥WMO/TD-No.1273，WWRP-THORPEX No.5.

Ritchie H，Beaudoin C.1994.Approximations and sensitivity experiments with a baroclinic semi-Lagrangian spectral model［J］.Mon Wea Rev，122:2391-2399.

Shutts G J.2004.A stochastic kinetic energy backscatter algorithm for use in ensemble prediction systems［R］∥ECMWF tech.memo.no.449，ECMWF，ShinfieldPark，Reading，BerkshireRG2 9AX，UK.

Shutts G J.2005.A kinetic energy backscatter algorithm for use in ensemble prediction systems［J］.Quart J Roy Meteor Soc，131:3079-3102.

Titley H，Savage N，Swinbank R，et al.2008.Comparison between Met Office and ECMWF medium-range ensemble forecast systems［C］∥Meteorology R＆D technical report no.512，Met Office.

Toth Z，Kalnay E.1993.Ensemble forecasting at NMC:The generation of perturbations［J］.Bull Amer Meteor Soc，174:2317-2330.

Toth Z，Kalnay E.1997.Ensemble forecasting at NCEP and the breeding method［J］.Mon Wea Rev，125:3297-3319.

Toth Z，Desmarais J，Brunet G，et al.2005.The North American ensemble forecast system(NAEFS)［C］∥Abstract，the 1st THORPEX international science symposium，December 2004，Montreal，Canada.

Toth Z，Schultz P，Mullen S，et al.2007.Completing the forecast:Assessing and communicating forecast uncertainty［R］∥ECMWF workshop on ensemble prediction，7—9 November 2007，ECMWF，Shinfield Park，Reading，Berkshire RG2 9AX，UK，23-36.

Wang X，Bishop C H.2003.A comparison of breeding and ensemble transform Kalman filter ensemble forecast schemes［J］.J Atmos Sci，60:1140-1158.

Wei M，Toth Z，Wobus R，et al.2006.Ensemble transform Kalman filter-based ensemble perturbations in an operational global prediction system at NCEP［J］.Tellus，58A:28-44.

Wei M，Toth Z，Wobus R，et al.2008.Initial perturbations based on the ensemble transform(ET)technique in the NCEP global operational forecast system［J］.Tellus，60A:62-79.

Zhu Y，Iyengar G，Toth Z，et al.1996.Objective evaluation of the NCEP global ensemble forecasting system［C］∥Extended abstract，the 15th AMS conference on weather analysis and forecasting，19—23 August 1996，Norfolk，Virginia.

Zhu Y，Toth Z，Wobus R，et al.2002.The economic value of ensemblebased weather forecasts［J］.Bull Amer Meteor Soc，83:73-83.

Zhu Y，Toth Z.2008.Ensemble based probabilistic forecast verification［C］∥Extended abstract，the 19th AMS conference on probability and statistics，21—24 January 2008，New Orleans，Louisiana.