蔡氏电路中模拟电感的容差分析

冯明库

(广东技术师范学院电子与信息学院,广东广州510665)

1 引 言

混沌及其应用是非线性科学研究领域的一个热点.自然界和人类社会中的许多混沌现象都可用非线性代数方程或微分方程来表示,并可用混沌电路来加以模拟.由于混沌电路易于构造、操作控制和观察,因而混沌电路的研究不仅在电路系统,而且在整个非线性科学研究领域都具有深刻的意义.

在已有的混沌电路中,最典型的是美国Berkeley大学 Leon.O.Chua提出的蔡氏电路[1-4].因其是能产生混沌行为的最小、最简、可证明的三阶自治电路,而获得了最为广泛的研究.电路的混沌特性是由其元件参量确定的,只要元件的参量在可能的范围内取值,系统就可展现出周期现象和混沌现象.在已有的对原始蔡氏电路混沌现象的研究文献中[5-7],研究者多是探讨电阻阻值或电容容值改变时分岔现象产生的情形.即便是对含有模拟电感的蔡氏电路,也是探讨原蔡氏电路部分中的电阻电容取值改变时蔡氏电路系统经倍周期分岔走向混沌的过程[8-9],很少研究组成模拟电感的各元件对蔡氏电路系统中混沌现象的影响.

本文用模拟电感代替原蔡氏电路中的电感元件,深入讨论模拟电感中2个电阻元件和1个电容元件参量改变时,系统由倍周期分岔走向混沌的过程,并与原始蔡氏电路改变电阻元件产生混沌的情形做比较,发现电路的鲁棒性和倍周期过程丰富性的优劣.

2 基于模拟电感的蔡氏电路

原始的蔡氏电路是三阶自治非线性电路系统,由1个电感L,2个电容 C1和 C2,1个线性电阻 R0以及1个分段线性电阻 NR所组成,如图1所示.

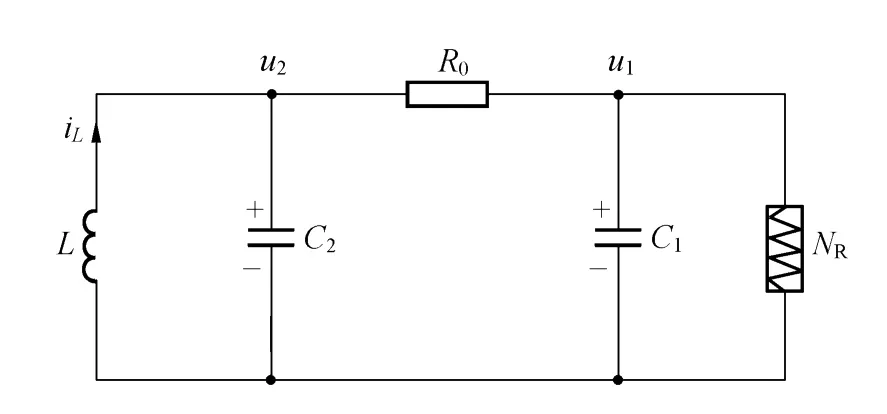
图1 原始蔡氏电路

蔡氏电路的三阶微分方程为

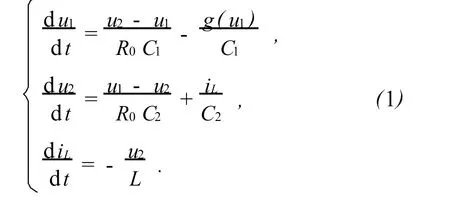
式中 u1和 u2分别是电容 C1和电容 C2两端的电压,iL为流过电感L的电流;g(u1)为蔡氏二极管NR的伏安特性函数,g(u1)=Gbu1+0.5(Ga-Gb)(|u1+E|-|u1-E|),其中 E为转折点电压,Ga和Gb为伏安特性曲线中2段不同折线线段的斜率,蔡氏二极管的伏安特性曲线见文献[2].

将图1中的电感L用模拟电感L′(图2中左虚线框内部分)替代,就组成了基于模拟电感的蔡氏电路(图2).图中右边的虚线框部分即为蔡氏二极管NR.

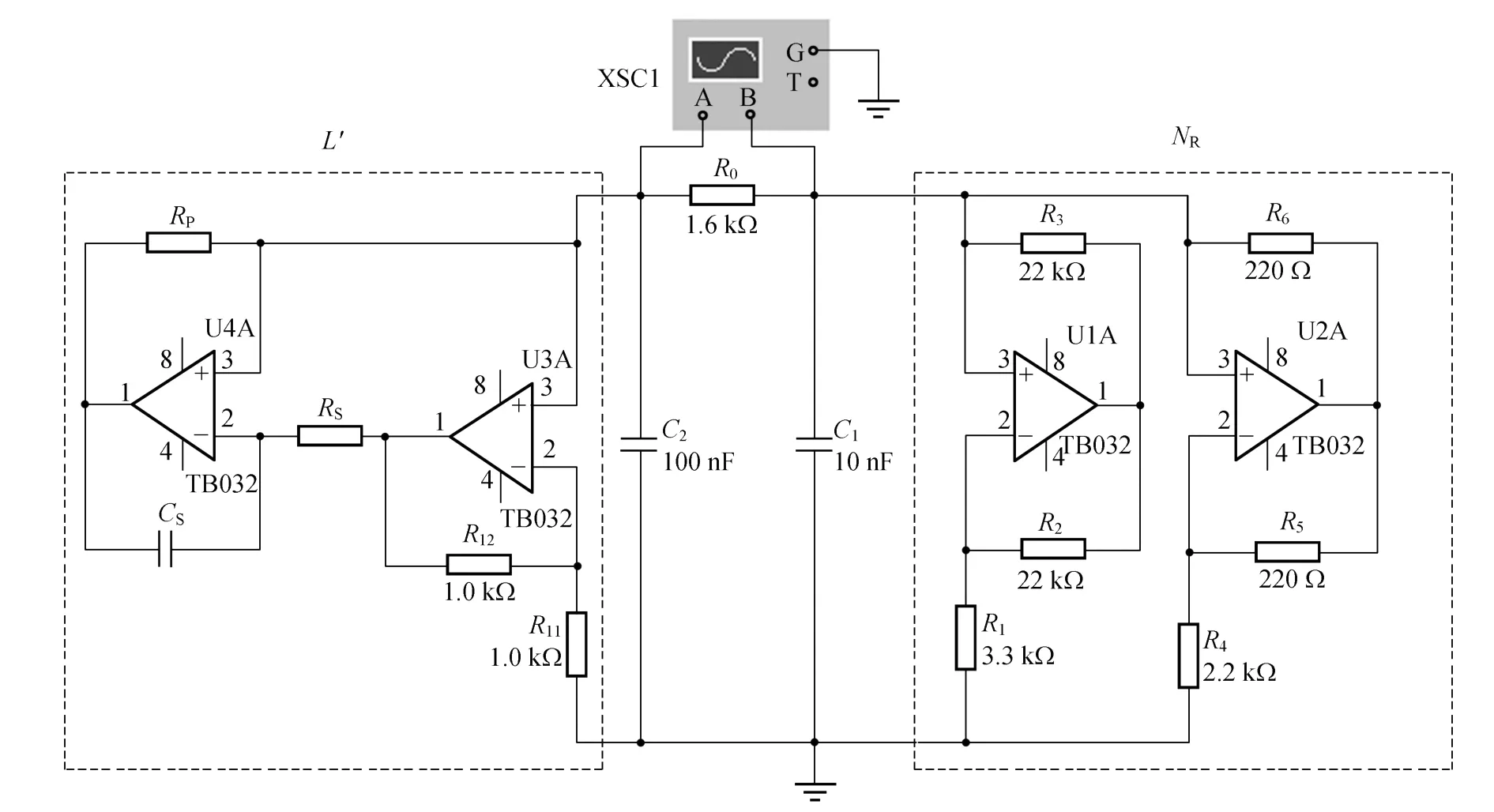
图2 基于模拟电感的蔡氏电路

利用理想运放的“虚短”和“虚断”的概念,可得出模拟电感的等效阻抗为

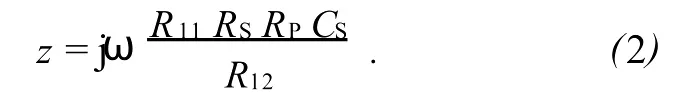
为了简化计算,在实验中,令 R11=R12=1 kΩ,则模拟电感的等效电感L′=RSRPCS.

3 仿真实验

对图1所示的原始蔡氏电路和图2所示的基于模拟电感的蔡氏电路,采用M ultisim仿真软件,分别调节电阻 R0和模拟电感中的 RS,RP和CS,观察不同组成的蔡氏电路经倍周期分岔走向混沌的过程,并计算各自的周期态时间和混沌态时间占整个分岔过程时间的百分比,比较它们的调节范围大小,给出电路分岔参量的容差数值.实验中,运算放大器的型号为 TB032,为了简化画图,±9 V的电源未画出.

3.1 原始蔡氏电路

按图1接线,电感取值18 m H,改变电阻元件 R0的阻值,得到电路经倍周期分岔进入混沌,乃至极限环的历程,见图3,横坐标为电容 C1上的电压u1,纵坐标为电容 C2上的电压 u2.当 R0大于2 108Ω时,电路经过简短时间振荡即进入平衡点[图3(a)是 R0=2 180Ω时的相图].当R0减小到2 018Ω时,电路进入稳定的一周期状态[图3(b)],继续减小阻值至1 978Ω,电路进入稳定的二周期状态[图3(c)],但再减小阻值,未能见到明显的四周期态和八周期态.当阻值减小到1 962Ω时,出现多周期状态.继续减小阻值至1 936Ω时,出现单涡卷混沌吸引子[图3(d)].当阻值等于1 933Ω时,电路出现双涡卷混沌吸引子[图3(e)].直到阻值为1 547Ω时,电路才开始出现极限环[图3(f)].电路的各个状态及其出现时相应的电阻阻值 R0见表1的第2列.

图3 原始蔡氏电路的倍周期分岔历程相图

3.2 基于模拟电感的蔡氏电路

按图2电路接线,取 R0的电阻值为1 600Ω,改变电阻 RS,RP和电容 CS的任一元件的值,同样观察电路经倍周期分岔走向混沌的过程.图4是改变电阻 RS时电路的各个状态图,横坐标为电容C1上的电压 u1,纵坐标为电容 C2上的电压u2.电路的各个状态及其出现时相应的电阻值RS,RP和电容值 CS见表1的第3～5列.

当电阻 RS等于750Ω时,电路开始起振,但随即进入稳定的平衡点[图4(a)].当阻值增大至812Ω时,电路进入稳定的一周期状态[图4(b)];当阻值增至1 197Ω时,电路进入稳定的二周期状态[图4(c)];继续增大阻值至1 251Ω时,四周期状态[图4(d)]开始出现,当阻值为1 258Ω时,八周期状态[图4(e)]出现,而四周期和八周期状态在图1所示的原始蔡氏电路很难观察到.当阻值变化到1 270Ω时,电路进入混沌态,开始出现单涡卷混沌吸引子[图4(f)];继续增大阻值到1 350Ω,双涡卷混沌吸引子[图4(g)]开始出现.在阻值增至1 800Ω时,混沌态结束,出现极限环[图4(h)].

由图3和图4可知,基于模拟电感的蔡氏电路的倍周期分岔历程更加丰富.从表1的数据可看出,基于模拟电感的蔡氏电路从倍周期开始至混沌态结束,整个阻值的调节范围为988Ω,而原始蔡氏电路仅为471Ω.基于模拟电感的蔡氏电路的倍周期过程可调电阻的调节范围(458Ω)占了整个分岔过程的46.4%,远大于原始蔡氏电路的17.4%,所以基于模拟电感的蔡氏电路的倍周期分岔过程更为丰富且易观察.从单涡卷混沌吸引子到双涡卷混沌吸引子再到极限环的整个混沌态分岔参量调节过程看,原始蔡氏电路为389Ω,而基于模拟电感的蔡氏电路达到了530Ω,调节范围更大,鲁棒性更强.从表1后3列 RS,RP和CS的分岔参量值来看,RS和 RP各个状态出现时的数值相同,三者的容差范围相同,这从式(2)也可以直接得出同样的结论.当改变 R0阻值,得到的三元件调节时的容差范围也是一致的,说明调节 RS,RP和电容值 CS的任何一个都能起到同样的效果.

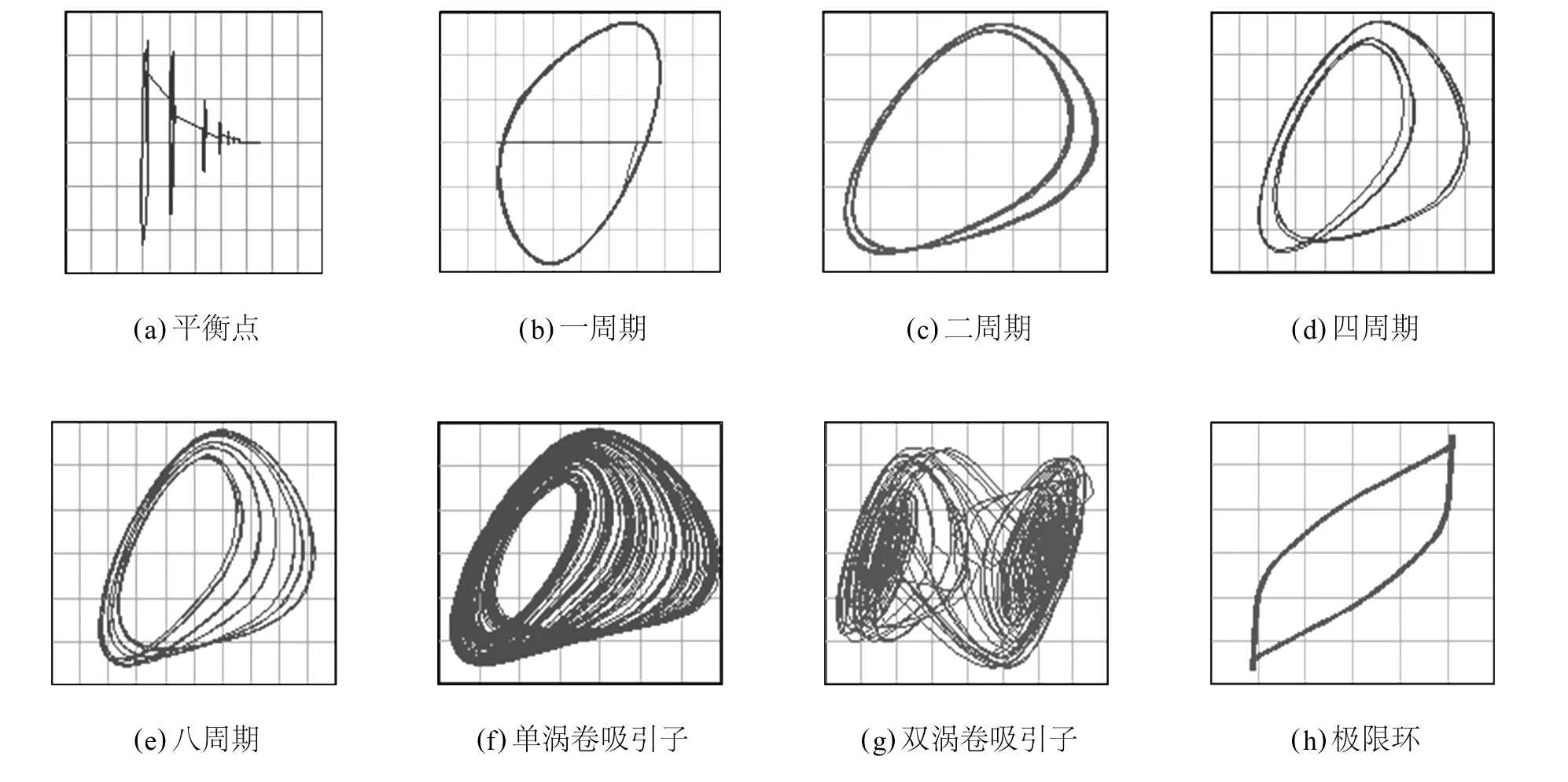
图4 基于模拟电感的蔡氏电路的倍周期分岔历程相图

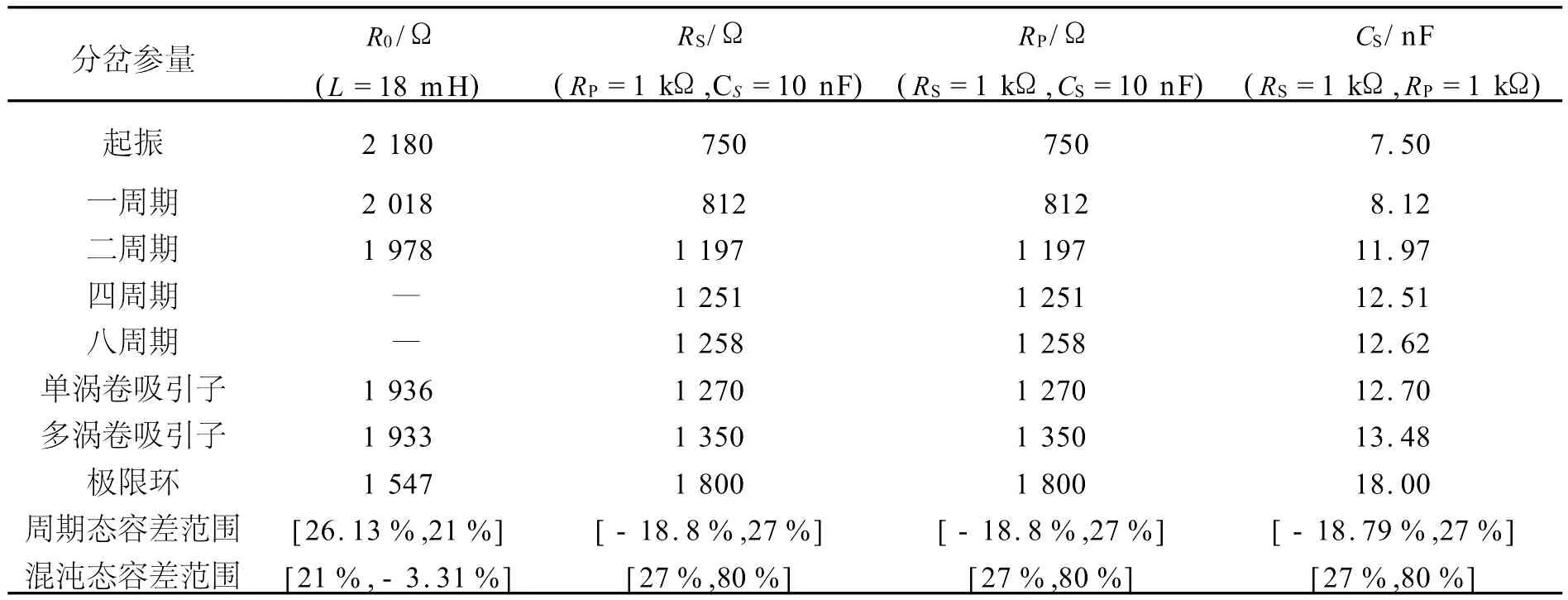
表1 电路的各个状态对应的分岔参量值及分岔元件的容差范围

4 硬件电路搭建及测试实验

按图2制成电路板后,固定其他元件值,只改变 RS的阻值,在 TDS 2022B数字存储示波器上记录下电容 C1和电容 C2上的 u1和 u2的相图,得到基于模拟电感的硬件蔡氏电路由倍周期分岔走向混沌的全过程,如图5所示.图5(a)是当 RS等于1 000Ω时,电路出现的一周期状态;当 RS等于1 200Ω时,出现图5(b)所示的二周期状态;图5(c)是 RS等于1 254Ω时出现的四周期状态;调节 RS等于1 265Ω,电路出现如图5(d)所示的八周期状态,由于内侧和外侧的4个周期状态不明显,改变示波器2个输入通道的灵敏度选择开关,放大图5(d)为图5(e)和图5(f).图5(e)是图5(d)的右半部分放大图,而图5(f)是对图5(d)右外侧的4个周期态的局部放大.可见,图5(d)中不明显的周期轨道在图5(e)和图5(f)中已清晰可见.图5(g)是 RS等于1 300Ω时出现的单涡卷吸引子,而图5(h)是 RS等于1 500Ω时电路呈现出的双涡卷吸引子;当调节 RS等于1 900Ω时,硬件电路出现如图5(i)所示的极限环.比较图5和表1的数据发现,硬件电路实验测试结果中 RS的各取值都在表1的各状态参量取值范围内,硬件电路实验测试结果与仿真实验数据吻合.

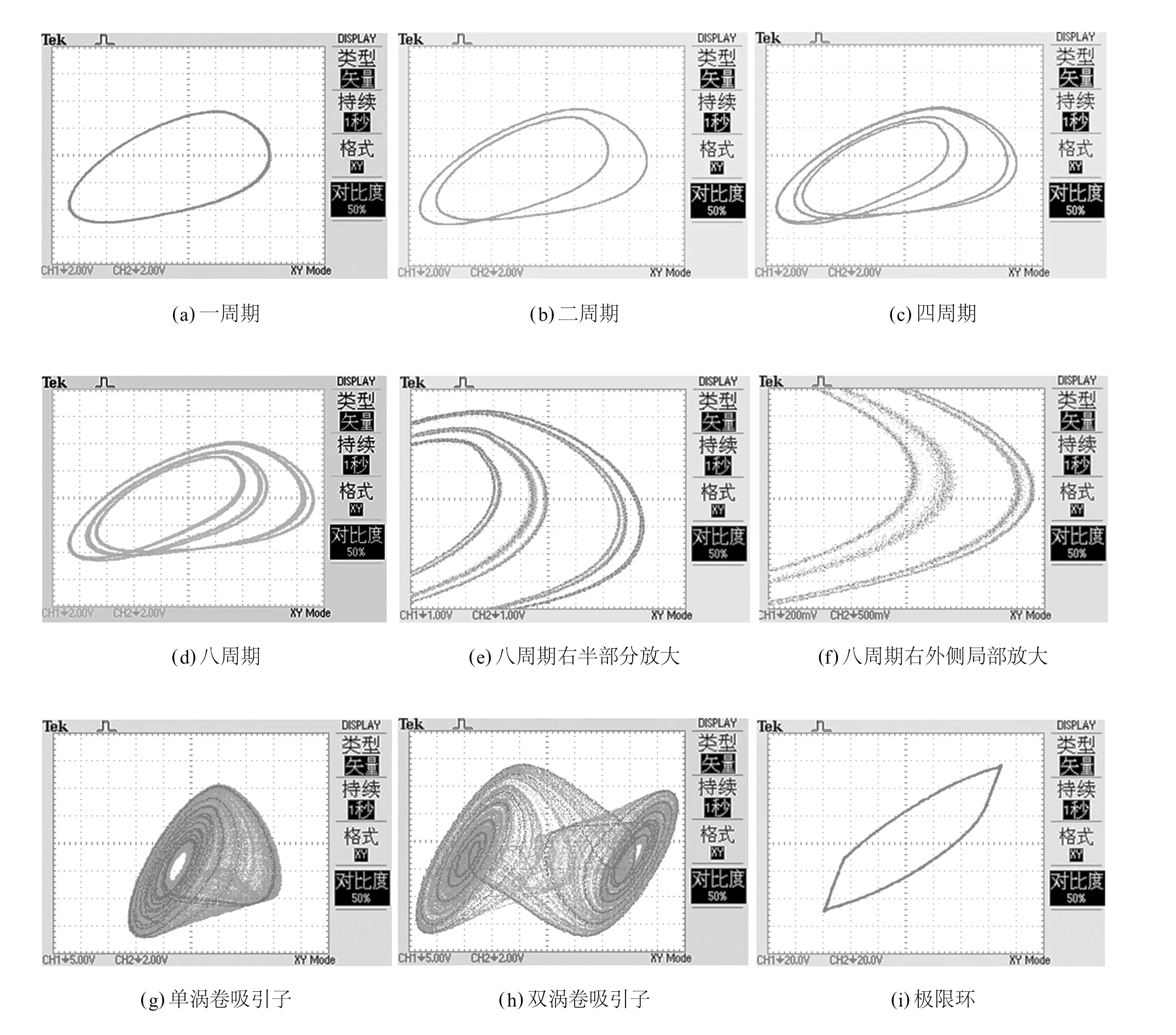
图5 基于模拟电感的硬件蔡氏电路的倍周期分岔相图

5 结束语

本文研究了基于模拟电感的蔡氏电路的倍周期分岔过程.由于原始蔡氏电路的电感元件被由运算放大器组成的模拟电感取代,因此硬件电路体积更小,便于集成.同时实验结果表明,此电路不但不影响蔡氏电路本身的特性,而且容易起振,更为突出的优势是分岔参量调节范围更宽,倍周期分岔现象丰富且易观察.

[1] Chua L O.Chua’s circuit 10 years later[J].International Journal of Circuit Theo ry and App lication,1994,22(4):279-305.

[2] Kennedy M P.Three steps to chaos——part Ⅱ:A Chua’s circuit p rimer[J].IEEE Transactions on Circuits and System sⅠ,1993,40(10):657-674.

[3] Zhong Guo-qun,Ayrom F.Periodicity and chaos in Chua’s circuit[J].IEEE Transactions on Circuits and System s,1985,32(5):501-503.

[4] Matsumoto T.A chaotic attractor from Chua’s circuit[J].IEEE Transactions on Circuits and Systems,1984,31(12):1055-1058.

[5] Huang An-shan.On boundsof the parametric range of bifurcation of Chua’s circuit[J].IEEE Transac-tions on Circuits and SystemsⅠ,1996,43(8):691-695.

[6] 罗荣芳,林土胜.蔡氏混沌电路硬件实现的容差分析[J].华南理工大学学报,2006,34(9):13-17.

[7] 卢元元,薛丽萍.蔡氏电路实验研究[J].电气电子教学学报,2003,25(3):67-69.

[8] 陈立宏,陈莉,高龙,等.改进蔡氏混沌电路的实现[J].物理实验,2009,29(6):35-37.

[9] 王宇清,杨文明.混沌电路电容参数的选择优化[J].物理实验,2009,29(2):45-46.