基于应变模态的桥梁损伤识别模拟分析

何文正，白 嵩，刁文菊

(重庆市建设工程质量检验测试中心)

1 应变模态推导

1.1 应变模态理论基础

桥梁结构的局部混凝土或钢筋损伤会导致局部刚度的下降，从而使损伤部位附近不大的区域内应变分布发生显著的变化，根据圣维南原理，在距损伤部位较远处的结构应变分布的变化将迅速衰减为正常状态，因此，我们可以通过实测的模态应变曲线，如果有应变分布发生明显的突变，则突变处所对应的结构位置就是损伤的位置，而且应变突变越大说明损伤也越大。

梁振动的微分方程为

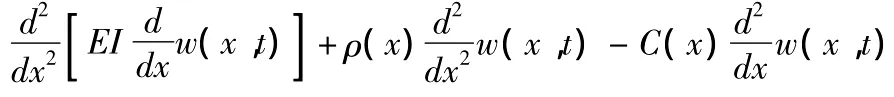
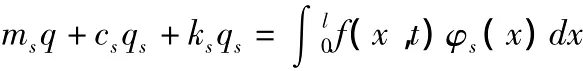
2 数值模拟

2.1 计算模型的建立

本次损伤识别数值模拟以钢筋混凝土简支T梁为例，T梁长L0=19.96m，计算跨径L=19.5m，梁高1.3m;截面形式如图1所示。

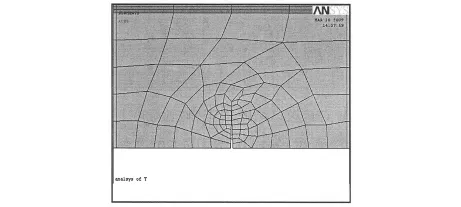
图1 跨中裂缝(工况1)

T梁除了跨中处的弯曲裂缝以外，同时在支点处还存在着由于剪切破坏产生的斜裂缝，此处考虑了以下几种工况，分别是:

工况(1):仅跨中处存在一条竖向裂缝，裂缝高0.4m，宽0.01m。工况(2):跨中处和支点处都只有一条裂缝，跨中裂缝高0.4m，宽0.01m，斜裂缝高0.4m，宽0.01m，倾角为45°。

工况(3):跨中处和支点处除了主裂缝外，在主裂缝两边各存在一条次裂缝，主裂缝高0.4m，宽0.01m，次裂缝高0.2m，宽0.01m。

跨中竖向弯曲裂缝及支点处斜裂缝的有限元模型见图1和图2所示，工况2下裂缝的有限元模型见图2、图3和图4所示。在计算中，模态分析过程的加载为梁本身自重，按照简支梁的边界条件对其一端支座施加水平和竖直方向的位移约束，对另一端支座施加竖直方向位移约束，并在翼缘和横隔板处施加横向的约束。

图2 支点处斜裂缝(工况2)

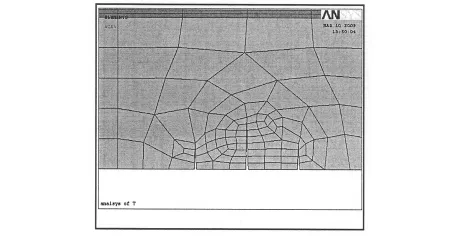
图3 跨中裂缝(工况3)

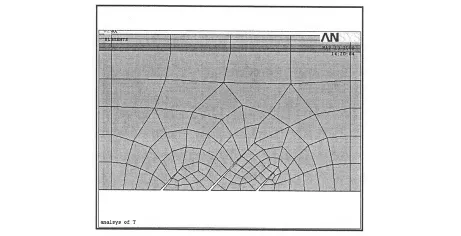
图4 支点处斜裂缝(工况3)

图5 T梁有限元模型(工况3)

各种工况下频率对比见表1:

根据表中可以看出，随着损伤数量的增加，固有频率下降的程度越大，但是仅仅依靠频率变化之能判断结构发生了损伤，而不能对损伤进行定位和判定损伤程度。

取梁底部测点，根据ANSYS分析数据绘制出前五阶应变模态曲线见图6。

从工况1、2、3的应变模态曲线可以看出，曲线在裂缝处出现了明显的尖峰突起，以此应变模态曲线能够准确地识别出梁多处损伤的位置;

从应变模态曲线可以看出，由于损伤的存在，应变模态曲线不再是一条光滑的曲线，在裂缝处发生了应力重分布，而在不远的地方应变又恢复到原来的大小。纵观工况1，工况2，工况3，我们可以看出第一、四阶应变模态曲线对跨中处损伤极为敏感，同时也能识别支点处单元的损伤，第二、三和五阶应变模态曲线对支点处单元损伤极为敏感，但是无法识别跨中处单元损伤，因此在实际检测工程中，应同时测取多阶应变模态。

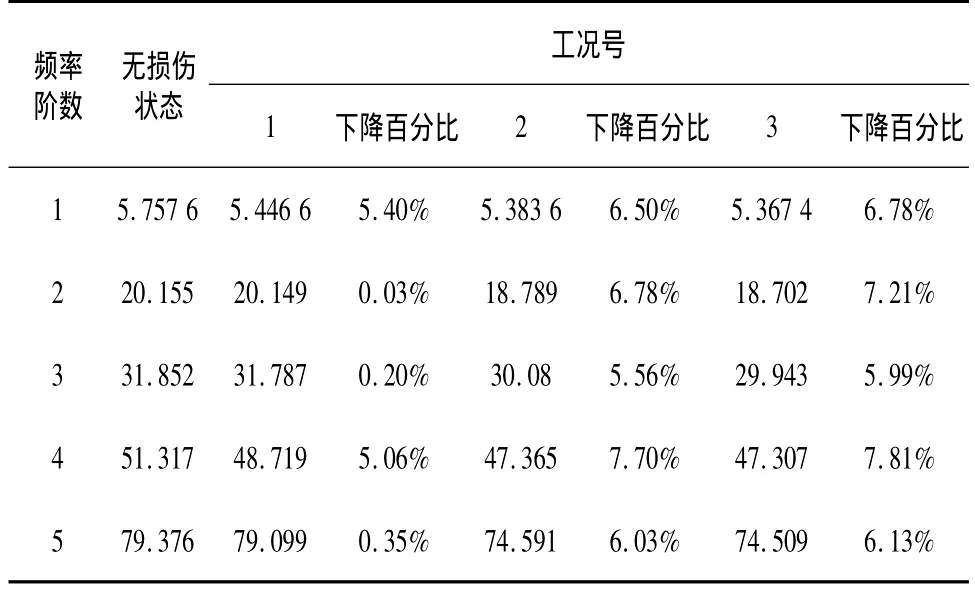
表1 各工况下频率下降对比

图7 应变模态曲线

3 结语

应变模态对局部损伤非常的敏感，应用应变模态方法检测桥梁损伤，能准确识别出桥梁损伤位置，一般不会产生误判;用应变模态识别损伤位置，不需要完好结构的数据，只要从现役结构采集数据即可，这对于一些建造时间久远又没有原始设计数据的桥梁结构来说提供了可行方案。此外应变能够直接测量，而不用通过差分计算得到，具有较强的抗噪能力，应变模态方法是桥梁损伤识别中值得推广的一种方法。

[1] 徐祖年，王柏生.基于振动测试的大跨桥梁损伤检测[J].合肥工业大学学报，2001，(11).

[2] 李国强，李杰.工程结构动力检测理论与应用[M].科学出版社，2002.