k－幂零矩阵的一个新性质

廖小莲，伍征斌，陈国华

(湖南人文科技学院数学与应用数学系，湖南娄底417001)

矩阵论是代数学的一个重要组成部分，而幂零矩阵作为一类特殊矩阵，具有很多良好的性质，它不仅在代数学本身中(如文献［1］)，而且在一些交叉学科如密码学(如文献［2－3］)中，都具有广泛的应用。目前，对以幂零矩阵为元素的全矩阵代数的子代数的研究成为代数学研究的中心课题之一。国内许多学者对幂零矩阵的性质已有较深入的研究，文献［4－8］分别对幂零矩阵的一些性质进行了探讨。本文在他们研究的基础上，进一步探讨幂零矩阵的性质，得到了k－幂零矩阵的一条新性质—n阶k－幂零矩阵的秩的取值范围。为了表述的方便，下面先引入几个定义和符号说明。

定义 1［4］394设 A ∈ Pn×n，若存在正整数 k ，使得 Ak－1≠0，Ak=0，则称A是幂零指数为k的幂零矩阵，简记为k－幂零矩阵。记表示一切 Pn×n中的 k － 幂零矩阵

集合。

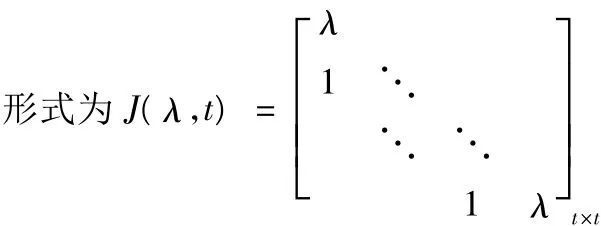
定义2的矩阵称为若当块，其中λ∈P，由若干个块组成的准对角矩阵称为若当形矩阵。记为满足下列条件的若当形矩阵J的集合:

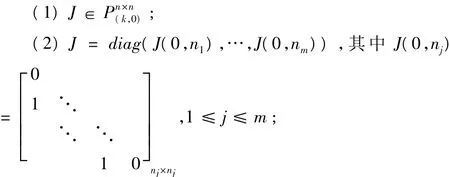
定义3［4］395整数分拆n=n1+n2+… +nm，其中n，ni∈ Z+，1≤ i≤ m，n≥ n1≥n2≥ … ≥ nm≥1，则 n1+n2+…+nm称为n的以首项为n1的有序分拆，或称其为n的一个首n1－有序分拆.(这里Z+表示所有的正整数集)。

1 预备知识

引理1 (若当定理)设A∈Pn×n，则必存在可逆阵T∈ Pn×n，使得:

T－1AT=J=diag(J(λ1，n1)，…，J(λn，nm)) ，

λ1，…，λn为 A∈ Pn×n的特征值(可能有相同)，称这样的J为A的Jordan规范型。

引理 2［4］395设 J(0，m) =Jm(0，m)=0且 Ji(0，m)≠0，(1≤ i＜ m)。

引理3 数域P上的k－幂零矩阵A的Jordan规范型具有形式 diag(J1，…，Jm) ，其中 Jj=J(0，nj) ，1≤j≤m，

2 主要结果

令 Jm={J ∈|J含有m块 J(0，k)} ，则 m 的取值范围为:，记

Jm中一个秩最大的若当形矩阵为Mm，则Mm确定n的一个首k－有序分。拆:

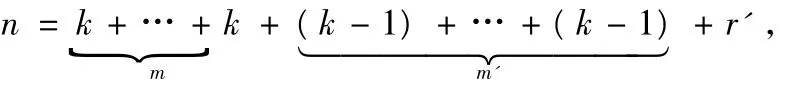
其中m为J(0，k)的个数，m'为 J(0，k－1)的个数(以下相同情况不再说明)，且 r'满足 (n－mk)≡r'(mod(k－1))。

事实上，设Mm确定n的一个首k－有序分拆:

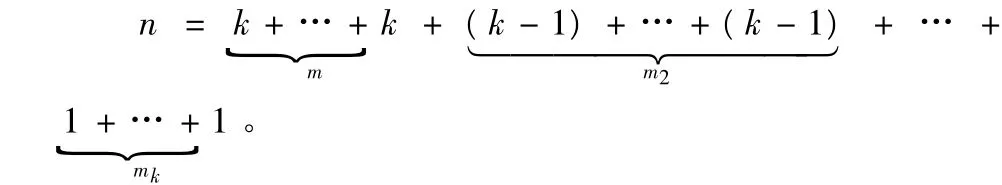
由于Mm是Jm中秩最大的矩阵，故mk=0或1。

对于任意l∈{1，2，…k－2}，在上述Mm确定n的一个首k－有序分拆中对应J(0，l)的个数为mk+1－l，于是若存在(不妨设i＜ j)使对应J(0，i)，J(0，j) 的个数 mk+1－i，mk+1－j均不为 0，则

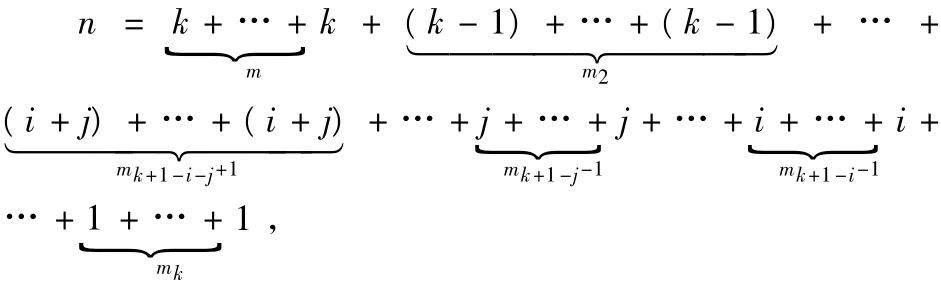
即在原Mm确定n的一个首k－有序分拆中，将对应J(0，i)，J(0，j) 的个数均减少1，而 i+j的个数增加1，显然

(2)当i+j＞ k－1时，记l=i+j－(k－1)，则i+j=l+(k－1)，设∈Jm，构造确定n的一个首k－有序分拆:易得r()=r(Mm)。

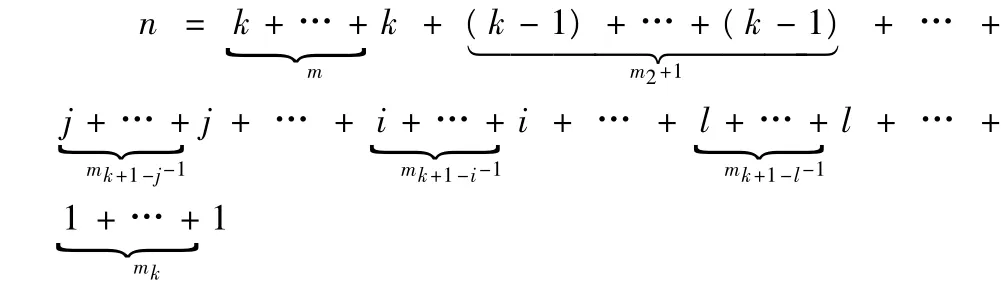
同理，若 i＞ j或i=j，则 i+j≤ k－1时，r() =r(Mm)+1);i+j＞k－1时，r()=r(Mm)。

综上所述，存在Mm确定n的一个首k－有序分拆:

且r'满足(n－mk)≡r'(mod(k－1))。

mm+1

首先，存在Mm+1确定n的一个首k－有序分拆:

其中 r″满足(n－m(k+1))≡r″(mod(k－1)) ，所以r(Mm)=m(k－1)+(k－2)+ φ(r)。r(Mm+1)=(m+1)(k－1)+(k－2)+φ(r)

mm+1于是的秩即A的秩的最大取值，而确定n的一个首k－有序分拆，所以r()=(k的最大值，易知存在Jm中的一个矩阵确定n的首k－有序分拆:所以r(A)的最小值为k－1。故A的秩的取值范围为:k－1≤

特别地，当 k=2，3 时，有:

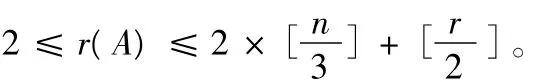
文献［4］的定理1的结论是本文定理的一种特殊情形。

3 主要结果应用

例1 求4阶方阵

的秩。

解:因为A3=0，Al≠0，l=1，2.所以A是3幂零矩阵，且4≡1(mo d3)，故r=1，k=3，代入定理的结论k－1≤秩(A)，得2≤秩(A)≤2，从而秩(A)=2.

［1］刘学质.用幂零指数的分布规律求Jordan基［J］.西南师范大学学报:自然科学版，2005，30(6):1005 －1008.

［2］李殿龙，骆吉洲.基于2－Jordan型幂零阵的Cartesian认证码的构造［J］.数学的实践与认识，2005，35(5):104 －109.

［3］李殿龙，郑宝东.利用有限域上2－幂零矩阵构作Cartesian认证码［J］.应用数学，2004，17(3):383 －388.

［4］林荣珍，江飞.3－幂零矩阵的相似等价类的计数［J］.数学研究，2006，39(4):394 －400.

［5］江明星.幂零矩阵的若干性质［J］.安徽机电学院学报，1999，14(2):77－79.

［6］韩道兰，罗雁，黄宗文.幂零矩阵的性质及其应用［J］.玉林师范学院学报(自然科学)2003，24(4):1－3.

［7］邹本强.幂零矩阵的性质［J］.science information，2007，(12):150－155.

［8］孙胜先，钱泽平.幂等和幂零矩阵的伴随阵的反问题［J］.大学数学，2006，22(5):114 －116.