基于遗传算法的相位差法波前检测piston误差

曹 芳，赵继勇，吴 桢

(1.南京理工大学紫金学院电光系，江苏 南京 210046;2.解放军理工大学通信工程学院，江苏 南京 210007;3.中国科学院国家天文台南京天文光学技术研究所，江苏 南京 210042)

综合孔径望远镜需要采用自适应光学系统实时校正失调参量［1］。目前应用于自适应光学的波前误差检测方法主要有:哈特曼传感器、剪切干涉仪、曲率传感器、相位恢复法。

相位差法(Phase Diversity)是相位恢复法的一个分支［1－4］，其思想是在成像系统的焦面和离焦位置上同时采集两幅图像，利用这一对图像恢复出光瞳上的波前分布。本文将PD方法用于光学综合孔径望远镜的失调误差检测，考虑到夏克哈特曼波前传感器对piston误差的不敏感，主要用于检测光学综合孔径望远镜系统的piston误差。

综合国外已有的研究成果，在相位差法检测系统失调误差时，多采用最小二乘法、共轭梯度法等非并行算法［5－9］，计算时间长，计算量大，当检测不同的波前相差时(如:piston、tip和tilt误差)由于相位差函数表达式的不同，使求导过程变得更加复杂，通用性不好;共轭梯度法要在初始值给定的基础上，进行函数寻优，如果初始值选定不当，具有陷入局部最小值的缺陷。遗传算法(Genetic Algorithm)是一种自适应优化问题求解方法，它起源于20世纪60年代对自然和人工自适应系统的研究。遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应人工智能全局并行算法。该算法所需附加信息少，检测不同的波前相差时，不受相位差函数表达式不同的影响，通用性好，这就为今后进一步深入检测tip和tilt误差预设了通道;遗传算法与初始值无关，具有其种群到种群的搜索特点。

本文首先对相位差法的原理和装置进行了阐述，将相位差方法与GA算法相结合检测系统piston误差，然后在计算机模拟望远镜成像系统的基础上，对一包含3个子孔径的综合孔径望远镜系统的piston误差检测，给出模拟实验检测结果，最后对结果进行了分析。

1 相位差法的原理

1.1 相位差法的原理

相位差法的思想是在成像系统的焦面和离焦位置上同时采集两幅图像，利用这一对图像恢复出光瞳上的波前分布。

从成像系统的离散数学模型出发，确定一个评价函数［4］，然后采用最优化方法对评价函数寻优，从而求出α，即piston像差。简化后的目标函数LM(α):

从(1)式可以看出，LM(α)只与α有关。在确定评价函数后，采用最优化方法可以求出使评价函数取最值时的自变量值，误差检测即可实现。本文使用遗传算法对该问题求解。

2 计算机模拟结果

2.1 成像过程模拟

模拟时，假设综合孔径望远镜由3个子望远镜组成，其子望远镜光瞳直径D=48 cm，焦距f=20 m，工作波长λ=600 nm。不同的失调量附加到每个子望远镜。图1给出了该综合孔径望远镜的光瞳示意图，表1为附加的实际系统失调量，假设系统存在piston误差，倾斜误差和噪声干扰。本文针对piston误差进行检测。

图1 综合孔径望远系统子孔径模拟Fig.1 Simulation of subapertures for an Aperture Synthesis Telescope

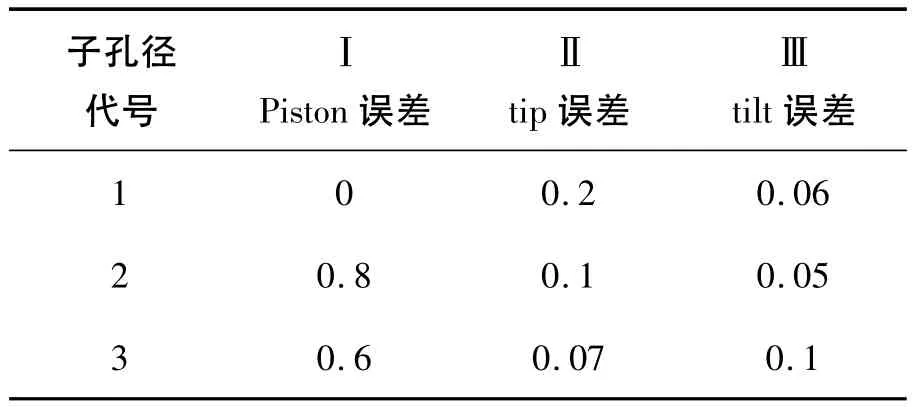
表1 附加在综合孔径望远镜子孔径间的失调误差 (单位:λ)Table 1 Misalignment errors assigned to subapertures in simulations

模拟含有表1失调误差的综合孔径望远系统在焦面和离焦位置(离焦量1.0 λ)分别采集两幅图像，其中离焦量Δw为1.0 λ，相应的离焦距离约为1.34 mm，在实验中对系统同时附加piston和倾斜误差，并考虑噪声影响。图2为模拟的目标图像，采样点为64×64。图3(a)和图3(b)分别为在焦面和离焦面上采集的图像，两幅图像均附加了1.0%的均值为零的高斯随机白噪声。

图2 模拟目标Fig.2 Simulated object

图3 通道1和通道2上CCD所采集到的图像Fig.3 Simulated images recorded by CCDs on channels 1 and 2

2.2 piston误差恢复程序

已知综合孔径望远镜的孔径函数Pn(u)，可求得系统两通道的未归一化的点扩散函数S1(u)和S2(u)，两扩散函数的未知量均为αn。对模拟得出的图3(a)和图3(b)采集处理后分别得到D1(u)，u∈χ和D2(u)，u∈χ。将S1(u)、S2(u)、D1(u)、D2(u)代入公式(1)中，求评价函数LM(α)取最优解时的自变量α即得出3个子孔径的piston误差。

这里采用GAs寻优［10－11］，算法流程见图4，参数设置如下:

(1)变异概率P=0.4，此时在父代遗传到子代时，可行解不是完全遗传，有40%的随机突变;

(2)解的范围 GenScale=［－1，－1;1，1］;

(3)种群规模FlockSize=500，每一代有2×FlockSize个个体。即此时每一代有2×500=1000个个体;

(4)基因个数(方程自变量的个数)GEN_NUM=2;

(5)表现型个数(方程输出个数，自变量对应的函数个数)，FAMILY_NUM=1;

(6)算法迭代次数STEP_NUM=50。

2.3 计算机模拟结果

选择均方根误差(RMSE)作为衡量波前恢复精度的标准，其定义为:

图4 遗传算法流程图Fig.4 Flowchart of a GA

式中，φ为估计值;φ0为真实值;Npupil为望远镜圆形孔径内的采样点数。

表2为恢复的piston误差值。图5给出了目标函数LM(α)随迭代次数的变化曲线，可以看出经过50次迭代后，结果趋于稳定。

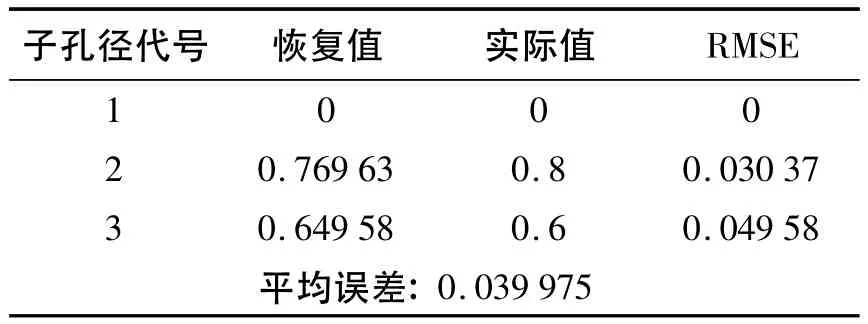
表2 piston误差恢复结果 (单位:λ)Table 2 Reconstructed piston errors

3 计算机模拟实验结果分析

对系统随机附加不同干扰做了18组实验，表3为全部实验结果汇总。

图5 目标函数LM(α)随迭代次数的变化曲线Fig.5 Object－function values varying with iteration numbers

从以上实验数据可知，系统仅存在piston误差的理想状态下，检测结果较好;加入噪声之后，检测结果受到一定的影响;当系统同时受到倾斜和附加噪声影响的情况下，检测结果误差增大。实验中发现对于噪声和倾斜误差同时存在的情况下，测量精度与子孔径的倾斜误差分配有关系，当加入的倾斜量的平均值相同而误差分配不同时，检测结果均方根误差也不同。另外倾斜误差与待检测的piston误差相比过大也会影响piston误差的检测。

表3 实验结果汇总 (单位:λ)Table 3 Simulation results

综合以上实验结果，系统的倾斜误差和成像过程中的噪声都会影响piston恢复精度，由于夏克哈特曼波前传感器对piston误差的不敏感，所以可以考虑先采用夏克哈特曼传感器检测并校正系统的倾斜误差，而后再采用PD方法进行系统piston误差的检测;对于系统噪声，可以考虑多帧叠加或者延长曝光时间提高信噪比以减小噪声对PD的测量精度的影响。

另外在对评价函数进行最优化处理时，GA算法的参数选择也会对检测精度产生影响，可考虑对此算法进行优化提高精度。

最后在数字图像处理过程中引入的圆整误差，也会降低检测结果的精度，这种误差是不可避免的。

计算机模拟验证了GA算法与相位差法的结合可以较准确地恢复包含3个子孔径的综合孔径望远系统的piston误差。

4 结论

本文在介绍相位差波前检测方法的基础上，研究了应用于相位差波前传感技术的优化算法，提出了基于相位差波前检测方法与人工遗传算法相结合，进行综合孔径望远系统piston误差的检测。遗传算法的使用为今后进一步深入检测tip和tilt误差预设了求解路径。同时，避免了陷入局部极小值情况。模拟实验结果证明，本文所提出的方法取得了良好的运行效果，能够达到期望的效果。

该方法对干涉望远镜的研究具有一定的参考价值。但还可以从以下几方面深入研究:GA算法本身的参数还缺乏定量的标准，目前采用的都是经验数值，所以如何找到最佳的参数，提高运算速度和精度，是今后值得进一步探讨的问题;另外还可以考虑对综合孔径望远镜子孔径的排列结构进行优化，以提高精度。

致谢:感谢朱永田老师、吴桢老师在学习中给予的指导和帮助，对赵继勇给予的帮助，在此一并表示感谢。

［1］曹芳，吴桢，朱永田.基于相位差法的光学综合孔径望远镜失调检测技术 ［J］.天文研究与技术——国家天文台台刊，2008，5(3):288－293.Cao Fang，Wu Zhen，Zhu Yongtian.Misalignment Sensing for Optical Aperture Synthesis Telescope Using Phase Diversity ［J］.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2008，5(3):288－293.

［2］张西亮，刘忠，钱声帮.恒星系统中暗弱伴星的高分辨率成像探测 ［J］.天文研究与技术——国家天文台台刊，2008，5(4):349－353.Zhang Xiliang，Liu Zhong，Qian Shengbang.Detection of Faint Objects in Multiple－star Systems with High－resolution Image Reconstruction Techniques ［J］. AstronomicalResearch ＆Technology——Publications of National Astronomical Observatories of China，2008，5(4):349－353.

［3］刘忠，金振宇，林京，等.30 m环形干涉望远镜 ［J］.天文研究与技术——国家天文台台刊，2006，3(1):64－72.Liu Zhong，Jin Zhenyu，Lin Jing，et al.Introduction to the 30 m Ringy Interferometric Telescope.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2006，3(1):64－72.

［4］李强，沈忙作.基于相位差方法的天文目标高分辨率成像技术研究 ［J］.天文学报，2007，48(1):113－120.Li Qiang，Shen Mangzuo.The Study of High－resolution Imaging of Astronomical Object Based on Phase－diversity Method ［J］.Acta Astronomica Sinica，2007，48(1):113－120.

［5］R A Carreras，S Restaino，D Duneman.A Laboratory Experiment Using Phase Diversity to Extract Higher Order Zernike Coefficients［C］//Timothy J Schulz，Donald L Snyder.Image Reconstruction and Restoration.Proceeding SPIE，1994，2302:323－329.

［6］R A Carreras，G Tarr，S Restaino.Concurrent Computation of Zernike Coefficients Used in a Phase Diversity Algorithm for Optical Aberration Correction［C］//Jacky Desachy.Image and Signal Processing for Remote Sensing.Proceeding SPIE，1994，2315:363－370.

［7］D V Lee，C Roggemann，B M Welsh，et al.Evaluation of Least－squares Phase－Diversity Technique for Space Telescope Wave－Front Sensing ［J］.Applied Optics，1997，36(35):9186－9197.

［8］R G Paxman，J R Fienup.Optical Misalignment Sensing and Image Reconstruction Using Phase Diversity［J］.Journal of the Optical Society of America(A)，1989，59(6):914－923.

［9］R G Pzxman，T J Schulz，J R Fienup.Joint Estimation of Object and Aberrations by Using Phase Diversity［J］.Journal of the Optical Society of America(A)，1992，9(7):1072－1085.

［10］周明，孙树栋.遗传算法原理及应用 ［M］.北京:国防工业出版社，1999.

［11］O Ritthoff，R Klinkenberg，S Fischer，et al.A Hybrid Approach to Feature Selection and Generation Using an Evolutionary Algorithm ［R］.Dortmund:University of Dortmund，2002.