粒子群算法在应急疏散中的应用研究

万江华， 卜凡亮

(中国人民公安大学安全防范系，北京 100038)

0 引言

目前关于应急疏散方面的研究很多，大多是研究疏散过程中物资、路径、车辆配置优化的，而在紧急情况下撤离疏散的很多因素当中，研究者们开始意识到研究人类社会行为对于提高公共场所的人群安全的重要性［1－5］。特别地，“非适应性人群行为”要对群体灾难的大部分受害者的死亡和受伤负责［6］。例如：2010年7月24日德国西部鲁尔区杜伊斯堡市电子音乐狂欢节时的踩踏事件;2010年11月22日柬埔寨钻石岛桥上的踩踏事故，都造成了巨大的人员伤亡和经济损失。为此我们需要研究突发事件中的非适应性人群行为，使我们能够准确的了解突发事件中人员的行为特征，以减少“非适应性人群行为”造成的人员伤亡，并且减轻紧急突发事件造成的损失和危害。

1 概述

1.1 非适应性人群行为

非适应人群行为指在紧急情况下人群会遇到的破坏性行为，如惊跑、推挤、碰撞、踩踏等［7］。一般分为3个层面来研究非适应性人群行为：个体、个体间的相互作用和个体与群体及环境的相互作用。这3个层面的分类并不是相互独立的，而是密切相关和交错的。

典型的非适应性人群行为一般有：模仿行为、竞争行为、排队行为、羊群行为、利他行为、领导跟随行为等。

1.2 粒子群算法的起源

粒子群算法(particle swarm optimization PSO)是群智能算法的一个重要组成部分。起初是由Eberhart和 Kennedy在1995［7］年提出。PSO 起源于人工生命，起初用于模拟鸟群飞行觅食行为，通过鸟之间的集体协作使群体达到最优。尽管每个个体的行为准则很简单，但组合成整个群体的行为将会是非常复杂的。由于粒子群算法概念简单、实现方便、收敛速度快、参数设置少，是一种高效的搜索算法，近年来受到学术界的广泛关注。

本文将对传统的粒子群算法进行改进，并对紧急情况下密集场所中群体的非适应性人群行为进行仿真，重点分析领导者行为对整个疏散过程的影响，为高人员密度场所的高效、快速的疏散提供相关的理论支撑。

2 改进的粒子群算法

2.1 标准粒子群算法

粒子群优化算法是一种模拟鸟群捕食行为的进化计算机技术。算法中的每个粒子可以看作解空间中的一个点，它根据自己的飞行经验和同伴飞行的经验来调整飞行，直到找到最优解。设粒子的种群规模为M，搜索空间的维数为D，每个粒子的维数为d(d=1，2，…，D)，则第 i(i=1，2，…，M)个粒子的位置可以表示为xid，它在飞行中所经历的最好位置叫做个体极值pid，整个种群所经历的最好位置叫做全局极值pgd，vid表示粒子沿着问题空间移动的粒子速度;那么粒子i根据下面的公式来更新自己的速度和位置［8－9］：

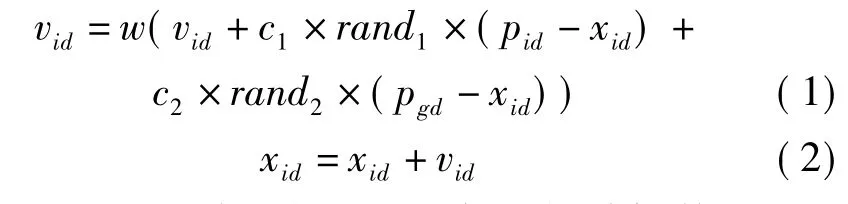
rand1和rand2是在范围(0，1)之间的随机数。c1和c2是学习因子;ω是惯性权重。

我们将对标准粒子群算法进行改进，对惯性权重进行优化，同时还加入了影响力因子，从而更好地模拟突发事件中的领导者行为。

2.2 领导者

现代社会大型公共设施(如：大型的购物中心、写字楼、体育场等)不断地增加，而在这些大型公共设施内都有相应的工作人员，我们将对这些工作人员进行培训，在参考文献［10］中，已经验证了人员培训与否对疏散时间的影响。在突发事件发生时，这些工作人员将成为整个疏散过程中的引导人员，称其为领导者。

在模型中引入领导者，假设这些领导者都知道最短的疏散路径，当发生突发事件时，领导者将会引导人员进行紧急疏散，即每个被疏散者都会与其周围的领导者进行信息交换。

在模型中，领导者可以看成是局部最优，但并不一定是全局最优，当被疏散者与领导者进行信息交换以后，可能收敛于局部最优，而不是全局最优。为了避免这种情况，我们将对韩江洪等2006年提出的自适应调整策略［11］进行改进，通过群体早熟收敛度和个体适应值来改变惯性权重的变化，使被疏散者最终达到全局最优。

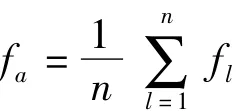
(1)fj优于 f'a，则

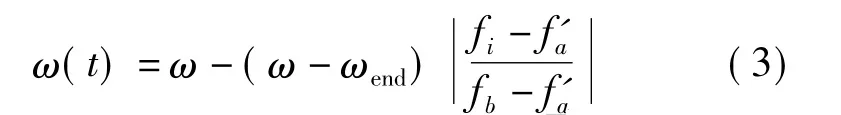
(2)fj优于fa但次于f'a，则惯性权重不变;

(3)fj次于 fa则

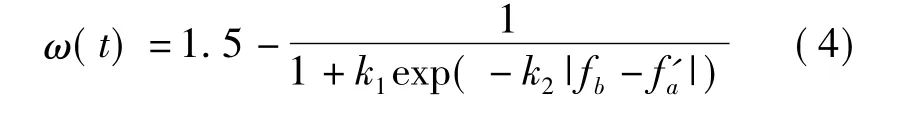
式(4)中的k1、k2分别为控制参数，k1控制ω的上限，k2控制调节能力。通过对3种粒子的惯性权重进行相应的调整，使粒子具有较强的全局或局部搜索能力，从而最终达到局部最优。

2.3 影响力

领导者由于性别、年龄、身体状况的差异，在引导疏散的过程中，其影响力大小不同，即其影响半径不尽相同，为不同的领导者分配不同的影响力因数，不过还可以通过物理的方法增加领导者的影响力，比如为领导者配备一些设备(扩音器等)，以增加领导者的影响半径。

在PSO算法中，学习因子c1、c2决定了粒子本身经验和群体的经验对粒子运动轨迹的影响，反映了粒子间的信息交流。在我们的模型中随着领导者影响力的增加，与领导者信息交流的粒子成倍的增加，这就增加了群体经验对单个粒子运动轨迹的影响。反之，粒子则更多地受到本身经验的影响。这说明c1随着影响力的增加而减小，c2随着影响力的增加而增加。我们将对A.Ratnawecra等2004年提出的利用线性调整学习因子取值的方法［12］进行改进，加入参数影响力R，影响力因子σR。影响力因子 σR=arctanR，则 c1、c2由公式(5)和(6)来确定。

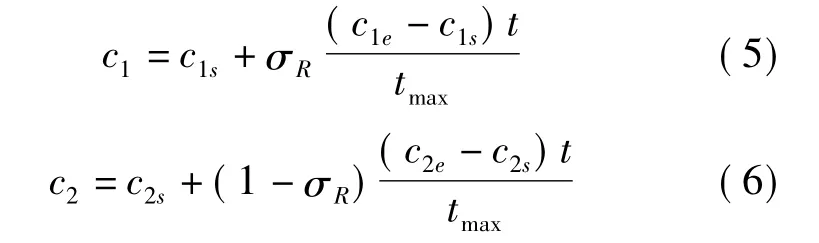
3 仿真实验与分析

本文将以超市为例进行仿真实验，我们将对无领导者与有领导者两种情况分别进行仿真，图1为超市的平面图。

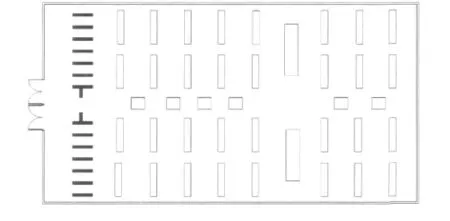
图1 超市平面图

3.1 仿真流程图(如图2)

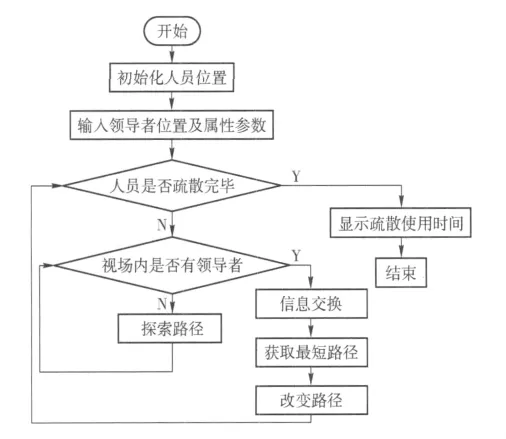
图2 仿真流程图

3.2 实验与分析

超市的初始人数设置为350人，由于超市的特殊性，我们将在每排货架之间安排一名领导者，每个领导者都有其相对固定的位置，在发生紧急情况时，每个领导者将到达事先规定好的位置(局部最优位置)，被疏散者将从领导者处得到最优疏散路径的信息。图3与图4分别为不同时刻时两种情况的疏散效果图。

通过不同时刻的仿真截图，在图3(c)(d)和图4(c)(d)中可以很明显地观察到排队行为，在图4(b)中还可以发现人群开始向领导附近聚拢，也就是领导跟随行为。通过对比图3和图4，可以发现图3中会出现一些游动人员，表明在无领导状态下，某些人员在疏散过程中会出现恐慌状态，而在图4中基本没有发现这种状况，图3(c)与图4(c)相对比，疏散路径发生了明显的变化，有领导者的仿真中疏散人员完全按照领导者处得到的信息进行有效率的撤离疏散。

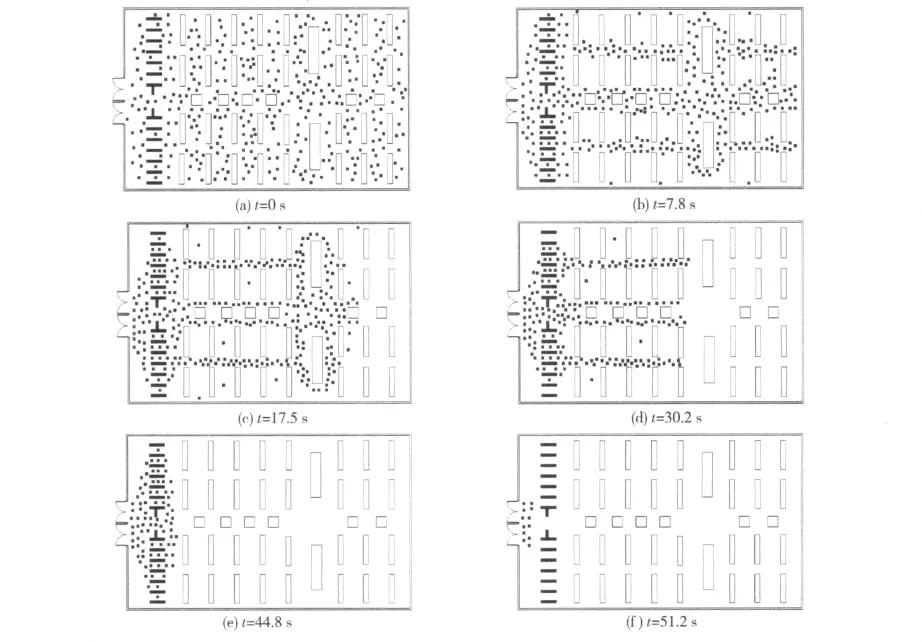
图3 无领导者情况的疏散效果图(●表示被疏散者)

我们在有领导者的疏散仿真中分别对领导者的分布、数量、影响力进行仿真，仿真实验数据见表1，仿真结果是我们对每种情况进行50次仿真取平均值所得到的，如图5～图7所示。

非常明显的，领导者均匀分布要比其他3种情况所需要的疏散时间少得多。在A条件下，疏散一开始的效率相对较高，而后期则变缓，主要由于前期受到领导者行为的影响，而后期则受到模仿行为等其他行为的影响;在B条件下，则是中期的变化有所加强;C条件下，则没有特别明显的变化。随着领导者分布的不同，所需撤离时间也有很大的区别，这就需要合理地分配领导者，使疏散所用时间最少。

图4 有领导者情况下的疏散效果图(●表示被疏散者;○表示领导者)

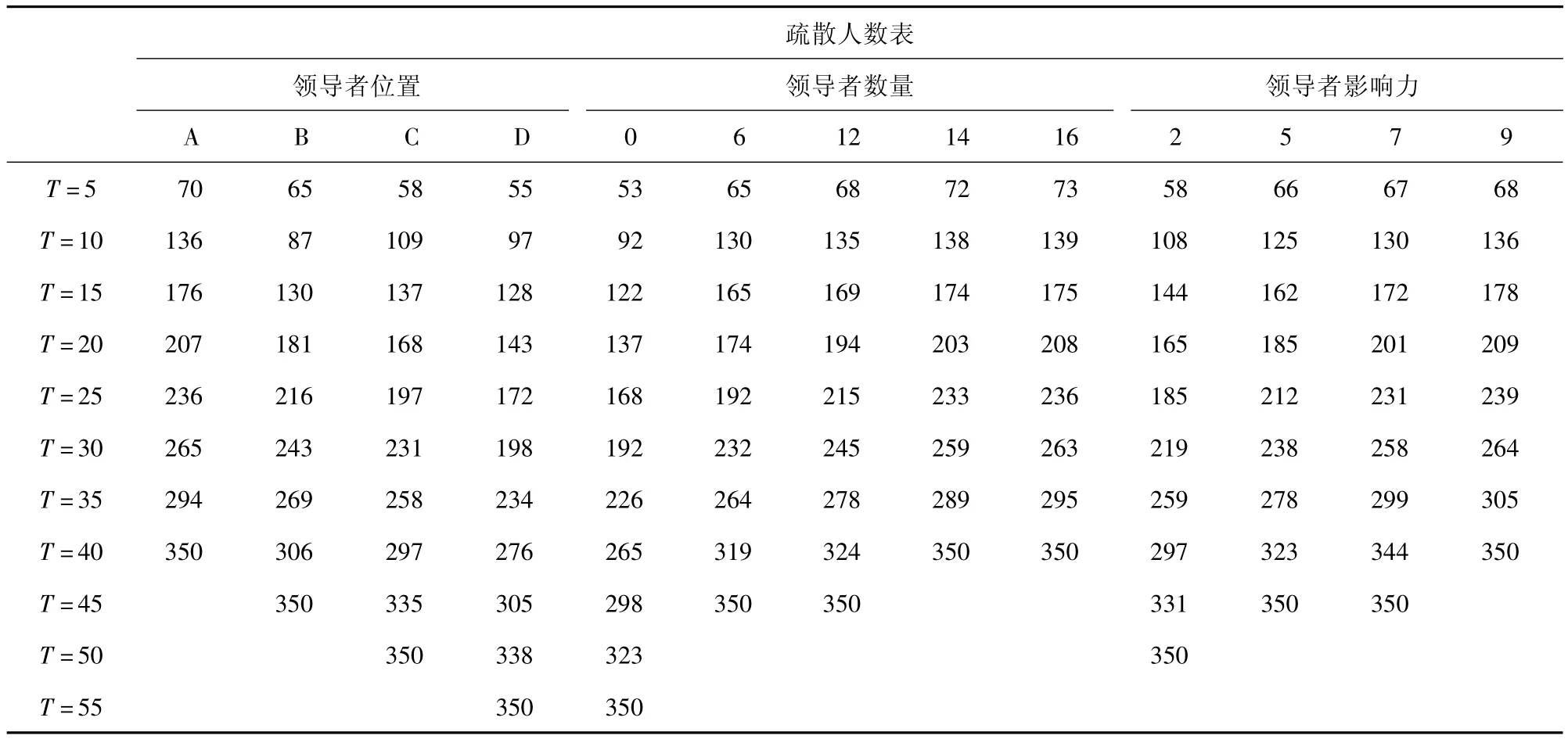
表1 不同条件下的疏散人数表(A：平均分布;B：分布在左半部分;C：分布在中间;D：分布在右半部分)

在模型中引入领导者后，不仅疏散路径会发生明显的变化，在疏散效率上也会有很大的提高。表1中有无领导者所需要的疏散时间有很大的差异，正如我们所预想的，领导者的数目越多则疏散所用的时间越短，理由非常简单，由于领导者知道如何进行疏散，并且具有更多的环境信息可以提供给被疏散者，因此，疏散时间将随着领导者在环境中的增加而减少。但并不意味着我们需要投入巨大的人力，图6可以看出当领导者数目达到一定数目时，疏散时间的增长率越来越小。

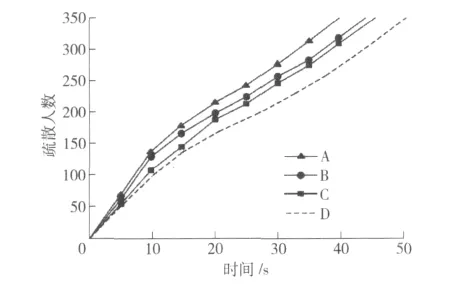
图5 领导者分布对疏散时间的影响

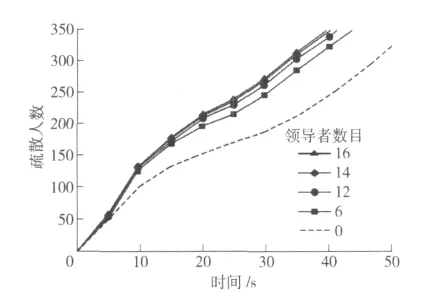
图6 领导者数量对疏散时间的影响

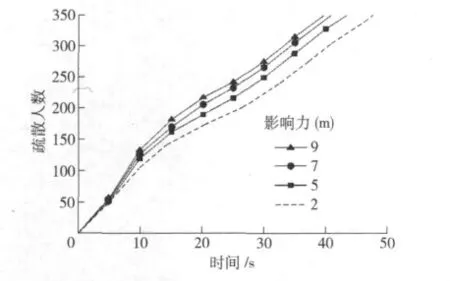
图7 领导者作用半径对疏散时间的影响

领导者本身的条件也将成为影响疏散的一个关键因素，在表1中可以看出，领导者的影响力越大，则疏散所需要的时间越短，但是疏散的速率影响并不是很明显(从图7可以看出)。但在现实中，当发生紧急情况，需要撤离的时候，往往我们周围的环境会变得非常的嘈杂，这样将直接影响领导者的影响力，所以在现实中，我们需要通过给领导者配备一些物理设备来加强领导者的影响力。从而节约疏散时间。

4 结论

在本文中，我们在传统的粒子群算法的基础上提出一种新的模型，并且对超市进行了疏散仿真。通过对仿真实验结果的比较，我们可以得到以下结论：领导者分布的不同对疏散时间的影响有很大的区别，并且疏散时间随着领导者数目的增加而减少;领导者的多少与建筑物的结构、功能有很大的关系，不同的建筑物需要我们配给不同数量的领导者。此外，我们还可以通过给领导者配备一些物理设备，以增加领导者的影响力，随着影响力的增加，所需要的疏散时间也在减少，从而实现高效、快速的疏散。

我们的模型仍有改进的空间，可以在模型中加入被疏散人员的属性参数，并且引入局部的突发事件，如：局部着火，建筑物倒塌以阻塞道路等。这可以令我们的模型更加完善，更加逼真地模拟现实中的疏散事件。

［1］ Bu Fanliang，Fang Hui.Shortest path algorithm within dynamic restricted searching area in city emergency rescue［C］.Proceedings 2010IEEE International Conference on Emergency Management and Management Sciences，2010：371 －374.

［2］ Bu Fanliang，Xie Qingmei.Research on emergency evacuation traffic trip generation forecasting based on logistic regression［C］.Proceedings 2010IEEE International Conference on Emergency Management and Management Sciences，2010：504 －507.

［3］ Bryan J.Human behavior and fire，in fire protection handbook［M］.Eighteenth edition，National Fire Protection Association，1997.

［4］ Fahy R，Proulx G.Collective common sense：a study of human behavior during the world trade center evacuation［J］.NFPA Journal，1995，87(2)：61.

［5］ Bu Fanliang，Chang Qin.Dynamic model of the mass event based on agenttechnology［C］. Proceedings 2010IEEE International Conference on Emergency Management and Management Sciences，2010：484－487.

［6］ Wilson G.Logic engineering in public safety，In Engineering for Crowd Safety Smith，R.and Dickie，J.(Eds.)，Proceedings of the International Conference on Engineering for Crowd Safety，London，UK，March 17－18，1993：231－237.

［7］ Pan Xiaoshan，Han C S，Dauber K，et al.Human and social behavior in computational modeling and analysis of egress［J］.Automation in Construction，2006，15(4)：448－461.

［8］ Clerc M.The swarm and the queen：towards a deterministic and adaptive particle swarm optimization［C］.Presented at Proceedings of the 1999 Congress on Evolutionary Computation，Washington，DC，USA，1999.

［9］ Clerc M，Kennedy J.The particle swarm-explosion，stability，and convergence in a multidimensional complex space［C］.IEEE Transactions on Evolutionary Computation，2002，6：58－73.

［10］ Bu Fangliang，Wan Jianghua.Lattice gas automatabased simulation ofevacuation［C］. Proceedings 2010IEEE International Conference on Emergency Management and Management Sciences，281 －284.

［11］ 韩江洪，李正荣，魏振春.一种自适应粒子群优化算法及其仿真研究［J］.系统仿真学报，2006，18(10)：2969－2971.

［12］ Ratnaawecra A，Halgamuge S.Self-organizing hierarchical particle swarm optimizer with time－varying acceleration coefficients［J］.Evolutionary Computation，2004，8(3)：47－48.