基于改进的蚁群算法的亚轨道再入飞行器弹道优化

张 斌，关世义，陈士橹

(1．西北工业大学航天学院，西安710068;2．北京机电工程研究所，北京100074)

0 Introduction

In recent years，reentry vehicle has attracted many researchers’attention．Many investigations have been done to improve applications for different reentry vehicles．The suborbital launch vehicle(SLV)is another reentry vehicle besides the reusable launch vehicle(RLV)［1］．It can be used for space tourism or as weapon system．However，no matter what purpose it can do，the reentry phase is very dangerous for both SLV and RLV．The heat and nonlinear aerodynamic force are very critical during this phase．Hence，the reentry trajectory planning and guidance always play an important role in the whole reentry phase．

The purpose of the guidance system is to control the vehicle to a desired destination with a sufficient energy state for approaching and landing by controlling the vehicle’s drag to dissipate excessive energy．The reference guidance method used on U．S．Space Shuttle is a major reentry method．By extending this approach，a new guidance law that schedules drag acceleration vs total energy has been investigated［2］．This method has more advantages than Space Shuttle’s approach and became the focus of researchers［3］．

For a decided task of reentry，two aspects must be considered:one is to choose and optimize reference drag acceleration profile which must minimize some indexes，another is to design approximate onboard controller to track the drag acceleration profile．Many papers have investigated these two aspects．In this paper，ant colony optimization(ACO)algorithm is used to optimize the reentry trajectory of SLV based on the grid model，and the LQR controller will be used to eliminate the disturbances．Simulation results show that feasibility of the optimal method and the effectiveness of control system operation while subjected to significant atmospheric variations．

1 Reentry dynamic model

Suppose the SLV is unpowered，wind disturbances are not considered，in terms of standard flight-path coordinates，the standard dimensionless point-mass equations of motion in the vertical plane over a spherical，non-rotating earth are described by following:

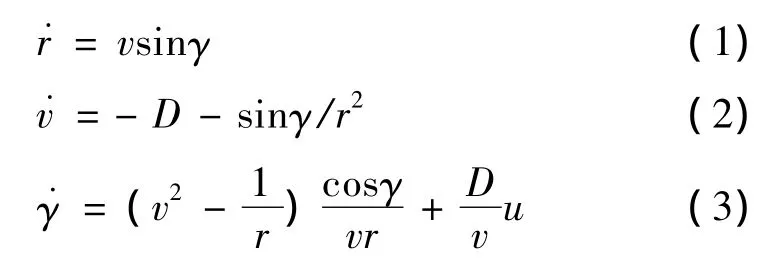
The derivation is with respect to the dimensionless timeτ．The control variable u is defined as the vertical component of the lift-to-drag ratio:

Whereσis the bank angle，CLand CDare the aerodynamic coefficients，respectively．

Define the negative total energy as an additional state variable

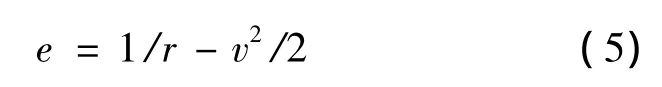
It represents the sum of kinetic and potential energy from the entry to landing site．If the heading path angle is very small，using the energy as an independent variable for guidance has more advantages and can also accurately predict the downrange distance and the total accumulated heat［3－4］．

2 Optimal trajectory

Suppose the SLV has higher lift-to-drag ratio，and the nominal attack angle vs velocity profile is available．The basic concept of the D－e profile is to divide the interval［e0，ef］into n－1 subintervals with n points．In each interval，［ei，ei+1］，the value of D is a linear function of e．The next step is to determine the value of D at each point，ei，to satisfy multiconstraints．Method of solving this problem is the ACO algorithm．

The ACO algorithm is another evolutionary algorithm，which is based on the behavior of real ants searching for food．Italian researcher found ants can always find the shortest path between nest and food．This natural phenomenon attracts his interest．Through depth study，he found out that ants deposit a chemical substance called pheromone on paths they have travelled．Ants tend to move toward path with high intensity pheromone．Hence，the shorter the path and the higher intensity of the pheromone，the more ants．The positive information feedback phenomenon makes ants to swarm into the shortest path．In the end，the optimized path is found by cooperation of ants［5］．

In artificial terms，ants construct solutions by making a number of probabilistic decisions．At beginning，there is no pheromone on any path，ants can only follow initial information．After some ants have found solutions，the pheromone information about every path is updated，the quantity of pheromone deposited by the ants depends on the solution quality found by them．In the course of optimization，the pheromone information left on paths can guide other ants in decision making．On the other hand，the pheromone deposition is not permanent，but will evaporate．Thus，over time，paths not used will have less pheromone and become less attractive，while those used frequently will attract ever more ants．The solution is searched［6］．

Compare to genetic algorithm，ACO algorithm has some advantages，such as simple，fast and suitable for discrete problems．However，like other intelligent searching algorithms，the ACO algorithm has same disadvantages，such as immature，slow convergence speed．To overcome these problems，one solution is to modify the deposited strategy of the pheromone．

The general rule of updating the pheromone is

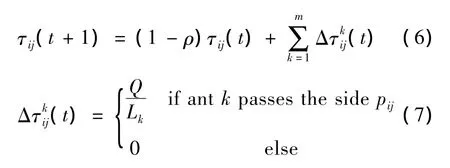
where m is the total number of ants，ρis the evaporation coefficient，Q is a constant，and Lkis the selected path by ant k at this iteration．Without any limit on pheromone at this formula，the ants will be able to get the local optimal solution，the key of improvement is to adjust the quantity of pheromone．

In the end of every iteration，the best solution will be saved，and after updating the pheromone，the pheromone on paths will be limited within［τmin，τmax］，τmincan avoid effectively algorithm stagnation andτmaxcan avoid one paths’pheromone is bigger than that of others’and the optimal solution could be ignored．Then，the updating rule of the min-max of pheromone is

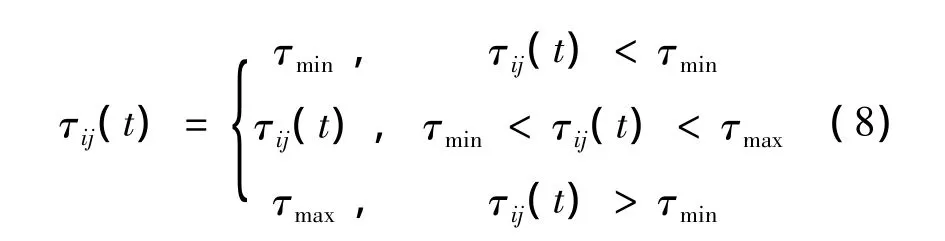
At the same time，as the problem scale becomes relatively large，constantρcould affect convergence speed of algorithm or the search capability．Hence，ρis adaptively increased as follows［7］:

Whereρmaxis the maximum evaporation coefficient．

For the reentry problem shown in Fig．1，the SLV reentry mission is to fly from point A to B．All the constraints form the entire reentry corridor．The possible flight paths must lie within the reentry corridor．The cost function is minimize total heat load

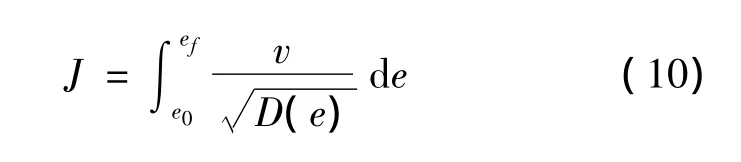
Drag vs energy guidance law needs divide solution space，transform the concerned indexes like the downrange distance or the total heat load from the integral form to summation form，then optimize the reference drag profile as a piecewise，linear function of the energy．Divide n points evenly on the energy axis，m points on the drag acceleration axis．According to the main theory about the ACO algorithm，repeat optimization process until optimal solution is searched．

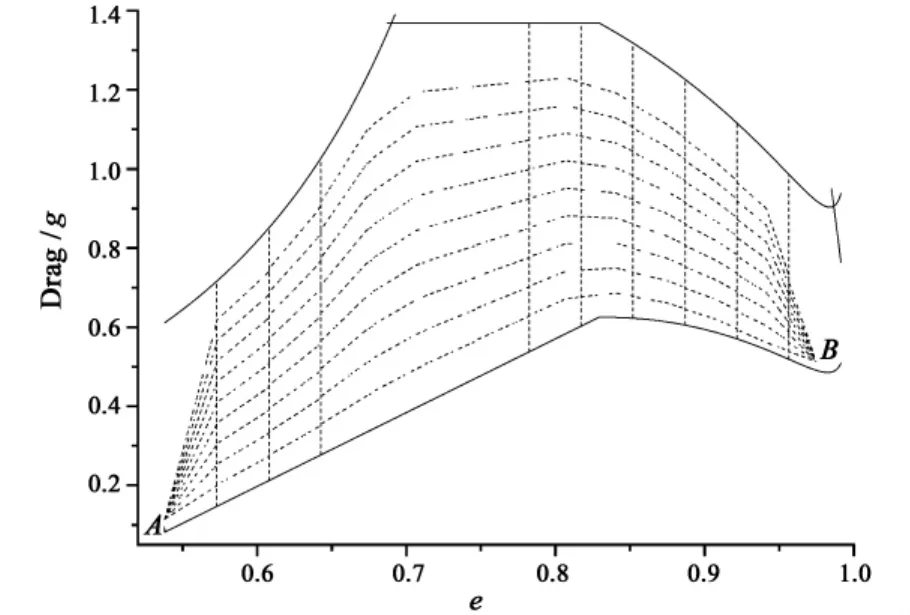
Fig．1 Illustration of the reentry optimization

3 Trajectory Control

Given the optimal drag vs energy profile，the nominal reference drag DR(e)can be determined．The corresponding reference drag derivatives and the reference control uRare derived as following:

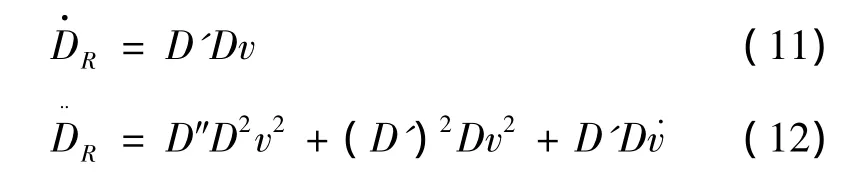
Where the dash indicates partial derivation with respect to e．Letequal to，which is derived with respect to timeτtwice，the reference control uRcan be obtained．

These reference values represent the nominal state trajectories that the control system is to maintain．However，the process of derivation is based on model assumption that does not exactly resemble reality．The in-flight drag trajectory will not perfectly match the reference one．The feedback stabilization is necessary to shape the drag error as desired．

The selected state variables are

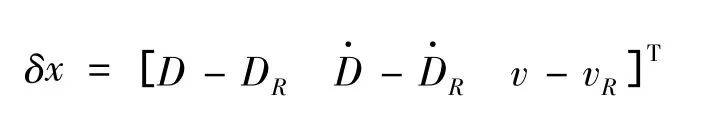
and the control error isδu=u－uR．For small deviations from nominal trajectory，a linear system can be defined as

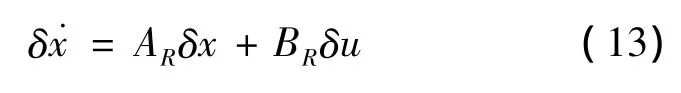
System and control matrices，ARand BR，are approximated at discrete energy values ekby numerically obtained constant matrices A(ek)and B(ek)，respectively．

The tracking control law used here is the linear time-varying feedback control laws

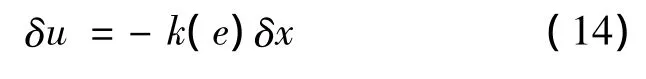
The gain k(e)is obtained offline with the linear quadratic regulator(LQR)approach at different discrete points along the reference trajectory e，and scheduled online with respect to e．Dukeman has demonstrated that LQR tracker has very good performance．More importantly，he showed that to track the reference trajectory，the LQR gains need not be recomputed for different missions for the same vehicle［8－9］．This means that one set of gains will work well for the same vehicle at different reference trajectories，and will be applicable to onboard trajectory generation．

The magnitudes ofσrequired by the vehicle flight dynamics are then obtained by

4 Simulation results

The trajectory is designed using aforementioned method for a SLV similar to X-33．The initial entry states are:h0=100km，v0=7500m/s，γ0=－0．5°．The terminal states are:hf=25km，vf=760m/s．The maximum allowable normal load nmaxis 2．5g．The maximum heat rate˙Qmaxis 544．3w/m2．The maximum dynamic pressure qmaxis 16280N/m2．The downrange distance is 5000km．The optimal result is shown in Fig．2．

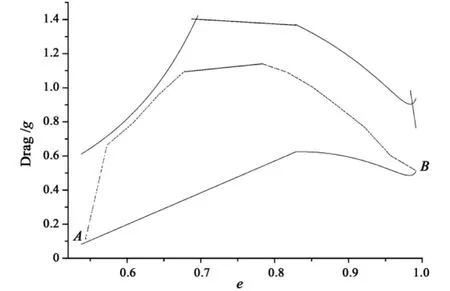
Fig．2 Optimal reentry trajectory

The optimal result shown in Fig．2 indicates that the trajectory is close to the upper constraint bound at the beginning．It indicates that the SLV needs a larger drag acceleration to consume its huge energy．Although this phase leads to high heat rate，it can reduce the accumulated heat load．After that，the SLV turns to constant drag acceleration in order to satisfy range requirement．At the end of the trajectory，the SLV adopts small drag acceleration that asymptotically approaches the lower constraint bound to meet the TAEM constraint．

Fig．3 Altitude vs downrange distance

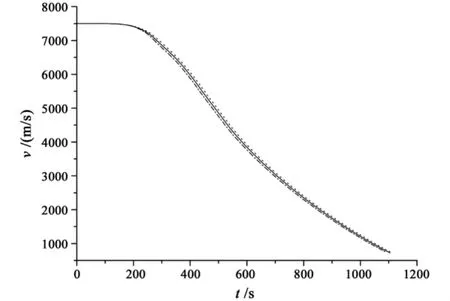
Fig．4 Velocity along the optimal trajectory

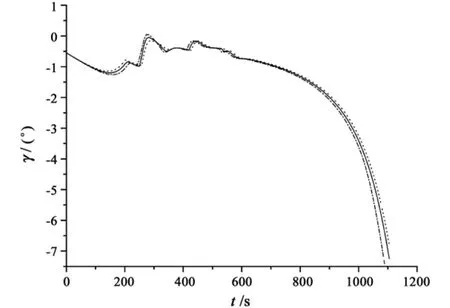
Fig．5 Path angle along the optimal trajectory

The performances of LQR tracker are shown in Figs．3 to 5．In the process of simulation，CL varies with±15%range．The simulation results demonstrate that although the terminal velocity or the path angle has litter variation，Fig．3 proves that the vehicle is able to achieve terminal altitude with satisfactory downrange distance．

5 Conclusions

Based on the discrete idea of the drag vs energy，the modified ACO algorithm is used to plan reentry trajectory．The optimal result shows that this algorithm is simpler and faster than other biotical algorithms for discrete problems．A linear feedback control law is designed to shape the drag error response to follow the nominal drag reference．Simulation results demonstrate that the control law effectively compensates for large atmospheric disturbances．

［1］Huang X，Bernd Chudoba．A trajectory synthesis simulation program for the conceptual design of a suborbital tourism vehicle［R］．AIAA Modeling and Simulation Technologies Conference and Exhibit，August 2005．

［2］Axel J Roemmeke，Albert Markl．Re-entry control to a drag-vsenergy profile［J］．Journal of Guidance，Control，and Dynamics，1994，17(5):916－920．

［3］Lu P．Entry guidance and trajectory control for reusable launch vehicles［R］．AIAA－96－3700，1996．

［4］Kurdjukov A P，Natchinkina G N，Shevtchenko A M．Energy approach to flight control［R］．AIAA－98－4211．

［5］Aditya P Apte，Wang B P．Using power of ants for optimization［R］．45th AIAA/ASME Structures，Structural Dynamics and Materials Confer，April 2004．

［6］Marco Dorigo，Vittorio Maniezzo，Alberto Colorni．The ant system:optimization by a colony of cooperating agents［J］．IEEE Transactions on Cybernetics，1996，26(1):1－26．

［7］Ye W，Ma D W，Fan H D．Algorithm for altitude penetration aircraft path planning with improved ant colony algorithm［J］．Chinese Journal of Aeronautics，2005，18(4):304－309．

［8］Greg A Dukeman．Profile-following entry guidance using linear quadratic regulator theory［R］．AIAA 2002－4457，2002．

［9］Shen Z J，Lu P．Onboard generation of three-dimensional constrained entry trajectories［J］．Journal of Guidance，Control，and Dynamic，2003，111－121．